RoPE中旋转位置编码的全部过程如图所示:
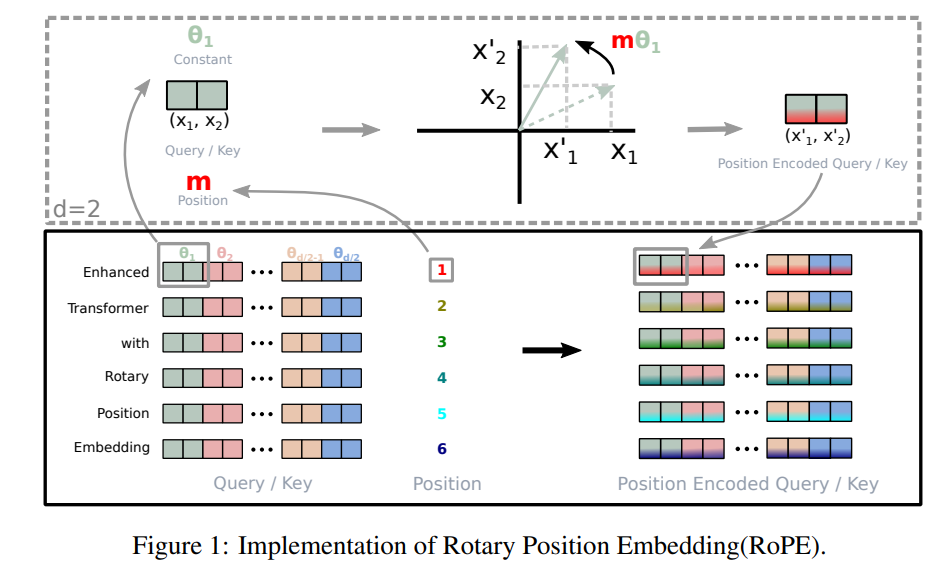
这里我以自己的理解解释一下这张图以及等式
q
m
=
f
q
(
x
m
,
m
)
=
(
W
q
x
m
)
e
i
m
θ
q_m=f_q(x_m, m)=(W_qx_m)e^{im\theta}
qm=fq(xm,m)=(Wqxm)eimθ
首先我们以二维为例子,为了方便我们令
m
=
1
m=1
m=1,再把
W
q
x
m
W_qx_m
Wqxm用
(
x
1
,
x
2
)
(x_1,x_2)
(x1,x2)表示,
q
m
q_m
qm用
(
x
1
′
,
x
2
′
)
(x_1',x_2')
(x1′,x2′)表示,就有了如下等式:
(
x
1
′
,
x
2
′
)
=
(
x
1
,
x
2
)
e
i
θ
(x_1',x_2')=(x_1,x_2)e^{i\theta}
(x1′,x2′)=(x1,x2)eiθ
这里我觉得不应该弄成等式,我转化成这样好理解一些:
(
x
1
′
,
x
2
′
)
<
=
(
x
1
,
x
2
)
e
i
θ
(x_1',x_2')<=(x_1,x_2)e^{i\theta}
(x1′,x2′)<=(x1,x2)eiθ
我们可以用两种理解去进行下一步的操作:
第一种:并入 e i θ e^{i\theta} eiθ
我们有
(
x
1
′
,
x
2
′
)
<
=
(
x
1
e
i
θ
,
x
2
e
i
θ
)
(x_1',x_2')<=(x_1e^{i\theta},x_2e^{i\theta})
(x1′,x2′)<=(x1eiθ,x2eiθ),采取的处理方式是先
x
1
e
i
θ
+
i
x
2
e
i
θ
x_1e^{i\theta}+ix_2e^{i\theta}
x1eiθ+ix2eiθ,单数取实部,双数取虚部这里有
x
1
e
i
θ
=
x
1
c
o
s
θ
+
i
x
1
s
i
n
θ
,
x
2
e
e
i
θ
=
x
2
c
o
s
θ
+
i
x
2
s
i
n
θ
x_1e^{i\theta}=x_1cos\theta+ix_1sin\theta,x_2e^{e^{i\theta}}=x_2cos\theta+ix_2sin\theta
x1eiθ=x1cosθ+ix1sinθ,x2eeiθ=x2cosθ+ix2sinθ
即
x
1
′
=
x
1
c
o
s
θ
−
x
2
s
i
n
θ
,
x
2
′
=
x
1
s
i
n
θ
+
x
2
c
o
s
θ
x_1'=x_1cos\theta-x_2sin\theta,x_2'=x_1sin\theta+x_2cos\theta
x1′=x1cosθ−x2sinθ,x2′=x1sinθ+x2cosθ
为什么
x
1
′
≠
x
1
e
i
θ
,
x
2
′
≠
x
2
e
i
θ
x_1'\neq x_1e^{i\theta}, x_2'\neq x_2e^{i\theta}
x1′=x1eiθ,x2′=x2eiθ ?都知道欧拉函数
e
i
θ
=
c
o
s
θ
+
i
s
i
n
θ
e^{i\theta}=cos\theta+isin\theta
eiθ=cosθ+isinθ,从欧拉函数中我们可以发现
e
i
θ
e^{i\theta}
eiθ是可以对应平面直角坐标系的,即
(
c
o
s
θ
,
s
i
n
θ
)
(cos\theta, sin\theta)
(cosθ,sinθ);从这里的公式来说
x
1
,
x
2
x_1,x_2
x1,x2表示的是标量,如果使用
x
1
′
=
x
1
e
i
θ
,
x
2
′
=
x
2
e
i
θ
x_1'= x_1e^{i\theta}, x_2'= x_2e^{i\theta}
x1′=x1eiθ,x2′=x2eiθ ,从某种意义上拓展了其维度,这也是我使用
<
=
<=
<=表示的原因;
第二种:转化为指数形式再展开
上面说了,标量直接与
e
i
θ
e^{i\theta}
eiθ从某种意义上来说相当于拓维,所以我们可以两两构成
γ
e
i
φ
\gamma e^{i\varphi}
γeiφ,再来与
e
i
θ
e^{i\theta}
eiθ进行计算,最后再把
γ
e
i
(
φ
+
θ
)
\gamma e^{i(\varphi+\theta)}
γei(φ+θ)转化为
(
x
1
′
,
x
2
′
)
(x_1',x_2')
(x1′,x2′) ;有
(
x
1
,
x
2
)
e
i
θ
=
>
γ
e
i
φ
⋅
e
i
θ
=
γ
e
i
(
φ
+
θ
)
=
>
(
x
1
′
,
x
2
′
)
(x_1,x_2)e^{i\theta}=>\gamma e^{i\varphi}·e^{i\theta}=\gamma e^{i(\varphi+\theta)}=>(x_1',x_2')
(x1,x2)eiθ=>γeiφ⋅eiθ=γei(φ+θ)=>(x1′,x2′)
γ
e
i
(
φ
+
θ
)
=
γ
(
c
o
s
(
φ
+
θ
)
+
i
s
i
n
(
φ
+
θ
)
)
=
γ
(
c
o
s
φ
c
o
s
θ
−
s
i
n
φ
s
i
n
θ
+
i
s
i
n
φ
c
o
s
θ
+
i
c
o
s
φ
s
i
n
θ
)
\begin{align} \gamma e^{i(\varphi+\theta)} & = \gamma(cos(\varphi+\theta)+isin(\varphi+\theta)) \\ & = \gamma (cos\varphi cos\theta - sin\varphi sin\theta + isin\varphi cos\theta + icos\varphi sin\theta) \\ \end{align}
γei(φ+θ)=γ(cos(φ+θ)+isin(φ+θ))=γ(cosφcosθ−sinφsinθ+isinφcosθ+icosφsinθ)
这里有 x 1 = γ c o s φ x_1 = \gamma cos\varphi x1=γcosφ, x 2 = γ s i n φ x_2 = \gamma sin\varphi x2=γsinφ
γ e i ( φ + θ ) = ( x 1 c o s θ − x 2 s i n θ ) + i ( x 1 s i n θ + x 2 c o s θ ) = x 1 e i θ + i x 2 e i θ \begin{align} \gamma e^{i(\varphi+\theta)} & = (x_1cos\theta-x_2sin\theta) + i(x_1sin\theta + x_2cos\theta)\\ & = x_1e^{i\theta} + ix_2e^{i\theta} \end{align} γei(φ+θ)=(x1cosθ−x2sinθ)+i(x1sinθ+x2cosθ)=x1eiθ+ix2eiθ
这里就得到 x 1 ′ = x 1 c o s θ − x 2 s i n θ , x 2 ′ = x 1 s i n θ + x 2 c o s θ x_1'=x_1cos\theta-x_2sin\theta, x_2'=x_1sin\theta+x_2cos\theta x1′=x1cosθ−x2sinθ,x2′=x1sinθ+x2cosθ
利用矩阵表示就是:
(
x
1
′
,
x
2
′
)
=
(
x
1
,
x
2
)
(
c
o
s
θ
s
i
n
θ
−
s
i
n
θ
c
o
s
θ
)
(x_1',x_2')=(x_1,x_2) \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix}
(x1′,x2′)=(x1,x2)(cosθ−sinθsinθcosθ)
这里旋转矩阵
R
R
R为
(
c
o
s
θ
s
i
n
θ
−
s
i
n
θ
c
o
s
θ
)
\begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix}
(cosθ−sinθsinθcosθ)
同时我们可以注意到
(
x
1
,
x
2
)
e
−
i
θ
=
>
γ
e
i
φ
⋅
e
−
i
θ
=
γ
e
i
(
φ
−
θ
)
=
>
(
x
1
′
,
x
2
′
)
(x_1,x_2)e^{-i\theta}=>\gamma e^{i\varphi}·e^{-i\theta}=\gamma e^{i(\varphi-\theta)}=>(x_1',x_2')
(x1,x2)e−iθ=>γeiφ⋅e−iθ=γei(φ−θ)=>(x1′,x2′)
得到的旋转矩阵就是
R
T
R^T
RT
引入到多维有旋转矩阵为:
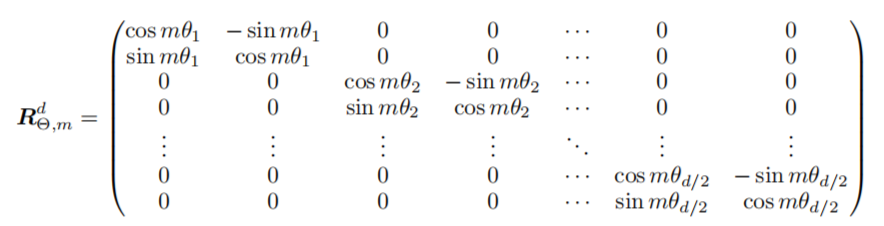
这里直接贴的原文,转置的原因为我这里的顺序与原文相反;
同时可以发现:
( c o s θ s i n θ − s i n θ c o s θ ) ( c o s θ s i n θ − s i n θ c o s θ ) T = ( c o s ( θ − φ ) s i n ( θ − φ ) − s i n ( θ − φ ) c o s ( θ − φ ) ) \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix} \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{pmatrix}^T= \begin{pmatrix} cos(\theta-\varphi) & sin(\theta-\varphi) \\ -sin(\theta-\varphi) & cos(\theta-\varphi) \end{pmatrix} (cosθ−sinθsinθcosθ)(cosθ−sinθsinθcosθ)T=(cos(θ−φ)−sin(θ−φ)sin(θ−φ)cos(θ−φ))
通过这个结论拓展到多维就可以得到:
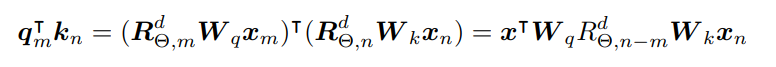
这里是原文中出现的错误 x T W q x^TW_q xTWq应该改为 x m T W q T x_m^TW_q^T xmTWqT;
也就是相当于 q m = f q ( x m , m ) = ( W q x m ) e i m θ = R m W q x m q_m=f_q(x_m, m)=(W_qx_m)e^{im\theta}=R_mW_qx_m qm=fq(xm,m)=(Wqxm)eimθ=RmWqxm k n = f k ( x n , n ) = ( W k x n ) e i n θ = R n W k x n k_n=f_k(x_n, n)=(W_kx_n)e^{in\theta}=R_nW_kx_n kn=fk(xn,n)=(Wkxn)einθ=RnWkxn
这里插入介绍一下旋转矩阵的快速计算技巧:

结合下面代码:
class RotaryEmbedding(tf.keras.layers.Layer):
def __init__( self, max_wavelength=10000, scaling_factor=1.0, **kwargs):
super().__init__(**kwargs)
self.max_wavelength = max_wavelength
self.scaling_factor = scaling_factor
self.built = True
def call(self, inputs, start_index=0, positions=None):
cos_emb, sin_emb = self._compute_cos_sin_embedding(inputs, start_index, positions)
output = self._apply_rotary_pos_emb(inputs, cos_emb, sin_emb)
return output
def _apply_rotary_pos_emb(self, tensor, cos_emb, sin_emb):
x1, x2 = tf.split(tensor, 2, axis=-1)
half_rot_tensor = tf.stack((-x2, x1), axis=-2)
half_rot_tensor = tf.reshape(half_rot_tensor, tf.shape(tensor))
return (tensor * cos_emb) + (half_rot_tensor * sin_emb)
def _compute_positions(self, inputs, start_index=0):
seq_len = tf.shape(inputs)[1]
positions = tf.range(seq_len, dtype="float32")
return positions + tf.cast(start_index, dtype="float32")
def _compute_cos_sin_embedding(self, inputs, start_index=0, positions=None):
feature_axis = len(inputs.shape) - 1
sequence_axis = 1
rotary_dim = tf.shape(inputs)[feature_axis]
inverse_freq = self._get_inverse_freq(rotary_dim)
if positions is None:
positions = self._compute_positions(inputs, start_index)
else:
positions = tf.cast(positions, "float32")
positions = positions / tf.cast(self.scaling_factor, "float32")
freq = tf.einsum("i,j->ij", positions, inverse_freq)
embedding = tf.stack((freq, freq), axis=-2)
# 这里 *tf.shape(freq)[:-1] 使用 model.fit 的话无法计算
# embedding = tf.reshape(embedding, (*tf.shape(freq)[:-1], tf.shape(freq)[-1] * 2))
embedding = tf.reshape(embedding, (tf.shape(freq)[0], tf.shape(freq)[-1] * 2))
if feature_axis < sequence_axis:
embedding = tf.transpose(embedding)
for axis in range(len(inputs.shape)):
if axis != sequence_axis and axis != feature_axis:
embedding = tf.expand_dims(embedding, axis)
cos_emb = tf.cast(tf.cos(embedding), self.compute_dtype)
sin_emb = tf.cast(tf.sin(embedding), self.compute_dtype)
return cos_emb, sin_emb
def _get_inverse_freq(self, rotary_dim):
freq_range = tf.divide(tf.range(0, rotary_dim, 2, dtype="float32"),tf.cast(rotary_dim, "float32"))
inverse_freq = 1.0 / (self.max_wavelength**freq_range)
return inverse_freq
结束!






















 1335
1335











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








