open3d 拉格朗算子法拟合平面方程

一、算法原理

1.算法步骤

对k一近邻点拟合平面，最小二乘法（平面过重心），拟定公式为
$$a(x-\frac{}{x})+b(y-\frac{}{y})+c(z-\frac{}{z})=0$$

1. 求重心
   $$\frac{}{x}=\frac{1}{N}\sum _{i=1}^{N}xi,\frac{}{y}=\frac{1}{N}\sum _{i=1}^{N}yi,\frac{}{z}=\frac{1}{N}\sum _{i=1}^{N}zi$$
2. 去重心化
   $$x=xi-\frac{}{x},y=yi-\frac{}{y},x=zi-\frac{}{z}$$
3. 拉格朗日乘子法求函数
   $$min(\sum _{i=1}^{N}i\ast \sum _{i=1}^{N}i)=\sum _{i=1}^N(ax+by+cz)\ast (ax+by+cz)$$

4 求偏导
1.4.1 对a求偏导
$$2xi\sum _{i=1}^{N}axi+byi+czi$$
1.4.2 对b求偏导
$$2yi\sum _{i=1}^{N}axi+byi+czi$$
1.4.3 对c求偏导
$$2zi\sum _{i=1}^{N}axi+byi+czi$$
1.4.3 矩阵化

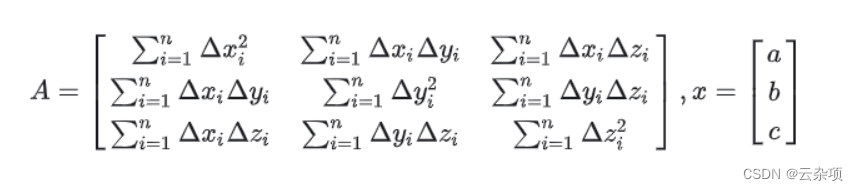
5. 求出最小特征向量

二、代码

import open3d as o3d
import numpy as np

def plane(pcd, normal_vector):
    """
    Args:将点云投影到平面
        pcd:  点云数据
        normal_vector:  方程法向量 mx + ny + sz + d = 0  传入[m , n, s, d]
    Returns: 投影后的点云数据
    """
    plane_seeds = []  # 保存投影后的点云数据
    # 获取平面系数
    m = normal_vector[0]
    n = normal_vector[1]
    s = normal_vector[2]
    d = normal_vector[3]
    # 将点云转换为数组
    points = np.asarray(pcd.points)
    for xyz in points:
        x, y, z = xyz
        """
        t = -(m*x + n*y + s*z + d) / (m*m + n*n + s*s)  # 计算参数方程参数
        """
        t = -(m * x + n * y + s * z + d) / (m * m + n * n + s * s)  # 计算参数方程参数
        """
        xi = m*t + x    # 计算x的投影
        yi = b*t + y    # 计算y的投影
        zi = s*t + z    # 计算z的投影
        """
        xi = m * t + x  # 计算x的投影
        yi = n * t + y  # 计算y的投影
        zi = s * t + z  # 计算z的投影
        plane_seeds.append([xi, yi, zi])  # 将投影后的点云添加到数组中

    plane_cloud = o3d.geometry.PointCloud()  # 使用numpy生成点云
    plane_cloud.points = o3d.utility.Vector3dVector(plane_seeds)  # points numpy数组

    return plane_cloud


if __name__ == '__main__':
    pcd = o3d.io.read_point_cloud('res/monkey.ply')
    points = np.asarray(pcd.points)  # 将点云转换为数组

    # 调用函数，生成离散点
    x, y, z = points[:, 0], points[:, 1], points[:, 2]
    # 求重心
    x0 = np.mean(x)   # 计算平均值
    y0 = np.mean(y)   # 计算平均值
    z0 = np.mean(z)   # 计算平均值
    # 去重心
    x = x - x0
    y = y - y0
    z = z - z0
    # ------------------------构建系数矩阵-----------------------------
    A = np.array([[np.sum(x * x), np.sum(x * y), np.sum(x * z)],
                  [np.sum(x * y), np.sum(y * y), np.sum(y * z)],
                  [np.sum(x * z), np.sum(y * z), np.sum(z * z)]])
    [D, X] = np.linalg.eig(A)  # 计算矩阵的特征值和特征向量的函数
    # 找到最小特征值的索引
    min_eigenvalue_index = np.argmin(D)
    # 获取对应的特征向量
    min_eigenvector = X[:, min_eigenvalue_index]
    print('平面拟合结果为：z = %.3f * x + %.3f * y + %.3f' % (min_eigenvector[0], min_eigenvector[1], min_eigenvector[2]))

    # 平面参数
    a, b, c, d = min_eigenvector[0], min_eigenvector[1], min_eigenvector[2], -min_eigenvector[0]*x0 - min_eigenvector[1]*y0 - min_eigenvector[2]*z0
    plane_cloud = plane(pcd, [a, b, c, d])  # 获得投影后的点云数据
    # ------------------ 可视化点云 -----------------
    plane_cloud.paint_uniform_color([1, 0, 0.0])  # 渲染颜色
    o3d.visualization.draw_geometries([pcd, plane_cloud])

三、结果

1.原点云数据

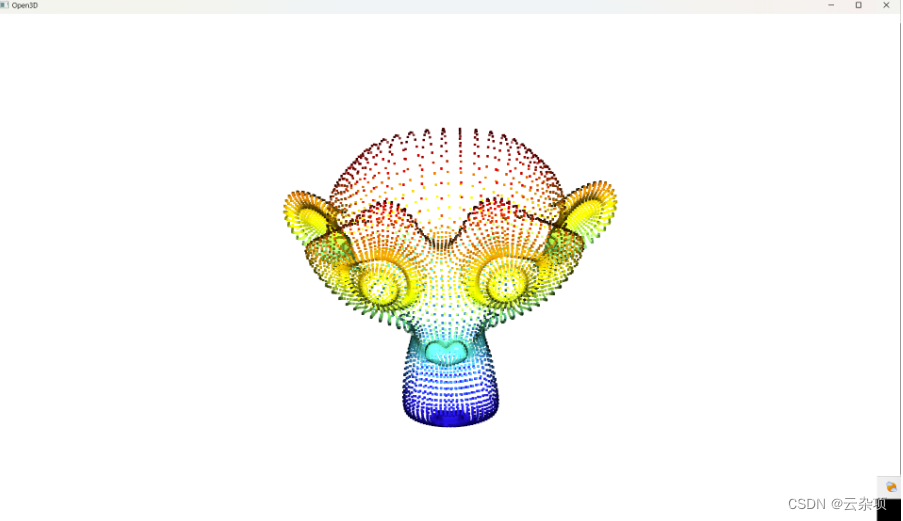
2.将点云拉格朗日乘子法拟合平面投影在该平面

四、相关数据

open3d 将点云投影到平面-CSDN博客：open3d 将点云投影到平面-CSDN博客
拉格朗日乘子法理论参考：最小二乘拟合平面(python/C++版) - 知乎 (zhihu.com)