马尔可夫性质（Markov property）

一、什么是马尔可夫性质

马尔可夫性质（Markov property）：指一个随机过程中当前状态的概率分布，只与前一个状态有关，而与之前的状态序列无关。

假设 { : t ∈ T} 是一个随机过程，其中 是在时刻 t 的状态，T 是时间集合。

那么，对于任意时刻 t 和任意状态 i、j 以及任意时刻 s < t，马尔可夫性质可以表述为：

给定当前时刻的状态，未来时刻的状态只与当前时刻的状态相关，而与过去时刻的状态无关。 

二、什么是马尔可夫链

马尔可夫链（Markov chain）：一个满足马尔可夫性质的随机过程，即给定当前状态的条件下，未来状态的概率分布仅依赖于当前状态，而与过去状态无关。具体来说，马尔可夫链是指一个状态空间和状态转移概率的序列，其中状态的转移满足马尔可夫性质。

 平稳分布（收敛性）：如果一个马尔可夫链具有平稳分布，那么在经过足够长的时间后，其状态将趋于一个固定的分布。马尔可夫链是否有平稳分布与其转移概率矩阵的性质有关。

三、马尔科夫链的状态转移矩阵代码例子

sample1：天气模型

import numpy as np

# 定义状态空间和转移概率矩阵
states = ['Sunny', 'Cloudy', 'Rainy']
transition_matrix = np.array([
    [0.7, 0.2, 0.1],
    [0.3, 0.4, 0.3],
    [0.5, 0.3, 0.2]
])

# 计算平稳分布
def stationary_distribution(transition_matrix):
    eigenvalues, eigenvectors = np.linalg.eig(transition_matrix.T)
    stationary_vector = np.real_if_close(eigenvectors[:, np.isclose(eigenvalues, 1)])
    stationary_vector = stationary_vector[:, 0] / np.sum(stationary_vector[:, 0])
    return stationary_vector

# 打印每一轮计算的过程
def print_iteration(iteration, dist):
    print(f"Iteration {iteration}:")
    for i in range(len(states)):
        print(f"状态 {states[i]} 的概率为 {dist[i]:.4f}")

# 初始化平稳分布
stationary_dist = np.ones(len(states)) / len(states)

# 打印初始状态
print("初始状态:")
print_iteration(0, stationary_dist)

# 迭代计算平稳分布
tolerance = 1e-5
max_iterations = 1000
for iteration in range(1, max_iterations + 1):
    new_stationary_dist = np.dot(stationary_dist, transition_matrix)
    print_iteration(iteration, new_stationary_dist)
    if np.allclose(new_stationary_dist, stationary_dist, atol=tolerance):
        print("达到平稳分布，迭代结束。")
        break
    stationary_dist = new_stationary_dist
else:
    print("未达到平稳分布，迭代次数达到最大值。")

# 打印平稳分布
print("平稳分布:")
for i in range(len(states)):
    print(f"状态 {states[i]} 的概率为 {stationary_dist[i]:.4f}")

三种天气状态：晴天（Sunny）、多云（Cloudy）和雨天（Rainy），运行上面的代码，会打印出状态转移矩阵，其中每一行表示从一个状态到所有其他状态的转移概率。

运行结果如下：

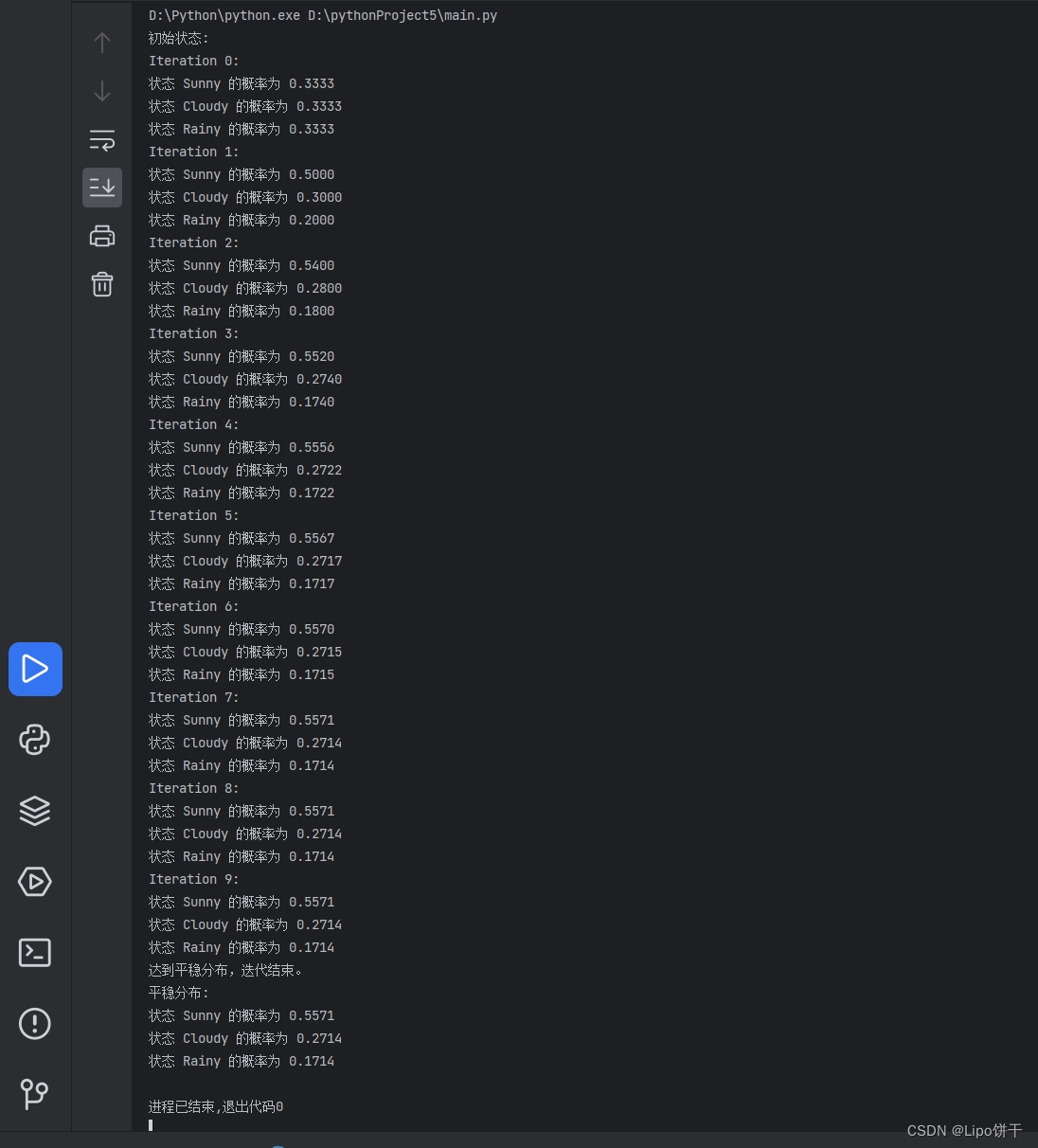
马尔可夫链具有平稳分布性质，可以看到在多次迭代后，各个状态的概率将趋于平稳分布。

平稳分布:
状态 Sunny 的概率为 0.5571
状态 Cloudy 的概率为 0.2714
状态 Rainy 的概率为 0.1714
 

sample2：投掷两枚骰子游戏

投掷两枚骰子游戏：每个骰子有六个面，分别标记为1到6。将状态定义为两枚骰子的点数之和，范围从2到12。状态转移矩阵的每个元素表示从一个状态转移到另一个状态的概率。

import numpy as np

# 定义状态空间
states = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]

# 初始化转移概率矩阵
transition_matrix = np.zeros((len(states), len(states)))

# 计算状态转移概率
for i in range(len(states)):
    for j in range(len(states)):
        # 计算两枚骰子点数之和为当前状态和下一个状态的概率
        dice_1 = np.arange(1, 7)
        dice_2 = np.arange(1, 7)
        transition_matrix[i, j] = np.sum((dice_1 + dice_2) == states[j]) / 36

# 打印状态转移矩阵
print("状态转移矩阵:")
for i in range(len(states)):
    for j in range(len(states)):
        print(f"从状态 {states[i]} 转移到状态 {states[j]} 的概率为 {transition_matrix[i][j]:.4f}")

运行结果：