《DIP数字图像处理》复习笔记--5.图像编码基础（图像压缩、冗余、编码定理，霍夫曼Huffman编码、香农Shannon-Fano编码、算术编码、LZW字典编码、行程编码、预测编码、变换编码，案例）

噢4u

已于 2024-11-08 20:22:49 修改

阅读量1.3k

点赞数 28

分类专栏：从0开始数字图像处理文章标签：数字图形处理学习笔记图像压缩图像编码霍夫曼编码香农编码 JPEG

于 2024-11-08 02:35:44 首次发布

本文链接：https://blog.csdn.net/m0_73752612/article/details/143610709

版权

从0开始数字图像处理专栏收录该内容

9 篇文章

订阅专栏

写在前面

DIP-Digital Image Processing-数字图像处理，是计算机图形学和计算机视觉的重要基础，本系列文章是根据“冈萨雷斯《数字图像处理》（第四版）”教材的顺序展开，解释数字图像处理中的重要知识点，同时也可作为期末复习笔记。

第一、二章序论、数字图形基础
第三章灰度变换与空间滤波
第四章频率域滤波
第六章彩色图像处理
第八章图像编码基础
第十-十一-十二章图像分割描述识别
上机作业

LZW编码（Lempel-Ziv-Welch)

图像压缩和数据冗余

图像编码的必要性

图像编码与压缩，本质上来说，就是对图像源数据按一定的规则进行变换和组合，从而达到以尽可能少的代码来表示尽可能多的数据信息。压缩通过编码来实现，或者说编码带来压缩的效果，所以，一般把此项处理称之为压缩编码。

一幅模拟图像必须经过脉码调制（PCM—Pulse Code Modulation)才能变成数字图像。（具体可见本专栏《1.数字图像基础--采样、量化、编码》）

设一幅活动图像的空间分辨率为N，灰度分辨率为b，时间分辨率为 $eq?f_B$ ，则在实时传输过程中，该图像在传输通道里的传输率至少应该为ρ=NbfB。
若N=512*512, b=8, $eq?f_B$ =25, 则ρ=52.4Mbps。这个值对于仅传输一幅图片来说代价太大了。

图像编码的目的：节省存储空间；减少传输时间；利于处理，降低处理成本。这也都符合在本专栏《1.数字图像基础》中所提到的数字图像处理的应用主要需要考虑的三方面因素。

图像数据经过编码压缩、传输、解码以及重建图像数据的流程如下图所示：

压缩率：

如等长码，5bit长度，n1即为5；压缩后的平均码长3bit，n2即为3。

相对数据冗余度：第一种编码方案下的数据集合相对于第二种编码方案下的数据集合的冗余量。

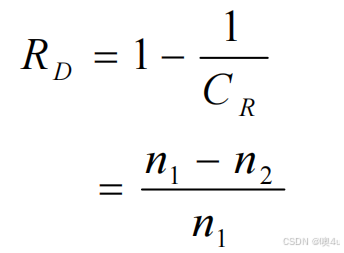
图像编码压缩分类

a) 从应用角度分类
- 静止图像编码，活动图像编码，二值图像编码；
b) 从信息保持程度角度分类
- 有损压缩（保真度编码，特征抽取编码）；
- 无损压缩（信息保持压缩，熵保持压缩，可以通过解码完全还原）；
c) 从具体的编码技术角度分类
- 空域法，变换域法；
- 预测编码，变换编码，统计编码，等。

图像数据的冗余

冗余大致分为三大类：

1）编码冗余（也称为信息熵冗余）
- 符号序列 -> 码字 ->（码字长度）
2）像素间相关性冗余
- 帧内像素信息冗余（空间冗余），帧间像素信息冗余（时间冗余）
3）心理视觉冗余
- 人眼对所有视觉信息并不是都具有相同的敏感度；
- 人眼的空间分辨率，时间分辨率

消除冗余能达到数据压缩的效果。

图像的编码质量评价

客观评价准则

客观评价主要通过数学计算评估处理后图像与原始图像的偏差，量化其失真程度。

总偏差：通过计算每个像素点的误差 e(x,y)=f(x,y)−f′(x,y) 的总和来衡量图像的整体偏差。
均方差：用于评估图像失真的平均水平，均方差越小，表示图像与原始图像的偏差越小。
均方信噪比：即信噪比的一种，通过衡量噪声信号和有用信号的平方和的比值来评估图像质量。
基本信噪比：用于进一步量化信号与噪声的比例，通过计算总功率的平方均值与噪声平方和的比值来量化信号完整度。

主观评价准则

主观评价准则则通过人为观察进行分类，对图像的视觉效果进行主观评分。通常采用1到7的评分表，其中1表示“很差”，7表示“很好”，根据观感来判断图像的质量。

这种主观评分有助于反映用户的真实感受，可以与客观指标结合，得到更全面的图像质量评价。

编码定理

如何度量编码方式的优劣？

编码定理的核心内容是在图像处理中如何度量编码方法的效率及信息熵等指标。

图像信息熵：设图像像素的灰度级集合为 $eq?d%20%3D%20%5C%7Bd_1%2C%20d_2%2C%20%5Cdots%2C%20d_m%5C%7D$ ，各灰度级出现的频率为 $eq?p%28d_i%29$ 。信息熵 H(d) 定义为：
$eq?H%28d%29%20%3D%20-%5Csum_%7Bi%3D1%7D%5Em%20p%28d_i%29%20%5Clog_2%20p%28d_i%29$ （信息论内容）
单位是比特/像素，表示图像的平均信息量。
平均码字长度：定义码字长度集合 $eq?%5C%7B%5Cbeta_1%2C%20%5Cbeta_2%2C%20%5Cdots%2C%20%5Cbeta_m%5C%7D$ （各个码字的长度数值），平均码字长度 R(d) 为：
$eq?R%28d%29%20%3D%20%5Csum_%7Bi%3D1%7D%5Em%20p%28d_i%29%20%5Cbeta_i$
单位是比特/像素，表示编码后的平均长度。
编码效率：编码效率 η 定义为信息熵和平均码字长度的比值：
$eq?%5Ceta%20%3D%20%5Cfrac%7BH%28d%29%7D%7BR%28d%29%7D%20%5Ctimes%20100%5C%25$
编码效率越高，表示编码越接近最佳。
冗余度：冗余度 $eq?R_d%20%3D%201%20-%20%5Ceta$ 表示编码中包含多少冗余信息，越小越接近无冗余编码。
熵编码：根据灰度值出现的频率分布，采用变长编码策略，使得出现频率高的灰度值用较短的码字表示，从而接近信息熵。

1）H(d)<<R(d)时，一定可以设计出某种平均码字长更短的无失真编码方法。
2）平均码字长小于H(d)的无失真编码方法不存在。

霍（哈）夫曼Huffman编码

基本哈夫曼编码系统框图：基于概率的前缀编码方法，无损，是一种统计编码。

算法

将灰度等级按概率大小进行排序（降序），每个灰度等级作为一个叶子结点，形成一棵树；
将两个根节点概率最小的树，合并（规则：这两个结点构造一个双亲结点，双亲结点的概率大小是两者之和）；重复1) 2), 直到只有一个树为止；
设所有左后代为0，右后代为1。

特点

优点：即时码；最优码（去除编码冗余）；
缺点：当需要对大量符号进行编码时，构造最优哈夫曼码的计算量会很大。

例

哈夫曼码的改型

亚最优编码方法，通过牺牲编码效率来换取编码计算量的减少。以下两种编码方式的平均码长都比传统哈夫曼编码的平均码长稍长：

截断哈夫曼编码：
- 对出现概率较高的符号使用传统的哈夫曼编码，对低概率符号则使用定长码表示。这种方法在某种程度上简化了低概率符号的编码。
- 截断哈夫曼编码可以通过在低概率符号前加上一个前缀，以区分高概率的短编码和低概率的长编码。
- 这种方法降低了部分符号的编码长度，但略微增加了平均码长。
平移哈夫曼编码：
- 在传统哈夫曼编码的基础上，对所有符号的编码加了一个固定的前缀或其他偏移，目的是减少某些情况下的运算复杂度。
- 平移哈夫曼编码相比标准哈夫曼编码，平均码长稍有增加，但通过添加偏移或前缀，能够简化硬件或软件实现中的某些计算。

Shannon-Fano编码

Shannon-Fano编码是一种基于概率的前缀编码方法，通常用于数据压缩。其算法的核心思想是将较高概率的符号用较短的编码表示，较低概率的符号用较长的编码表示，从而达到压缩的目的。无损。

算法

非递增排序（递减排序）：将所有消息（或符号）按出现概率从大到小排序。
概率分割：将排序后的消息集按概率之和相等或相近的原则分成两部分，这样每个子集的总概率尽可能接近。这种分割方式能够保证频率较高的符号集中在同一部分，以减少编码长度。
递归分割：对每个子集继续按同样的分割规则进行递归，直到每个子集中只剩下一个消息。每次分割后，都会生成新的子集，逐渐将每个符号分配到不同的路径上。
编码分配：在每次分割的过程中，将每个子集分别分配符号“0”和“1”。这样，通过路径上的分配，形成每个符号的二进制编码。

Shannon-Fano编码的优点在于其构建简单，且能够提供较为有效的数据压缩效果，但它在某些情况下（如符号概率非常接近）可能无法提供最优的编码方案。这种编码方法虽然接近哈夫曼编码的效果，但通常编码效率略低于哈夫曼编码。

例

算法编码

算术编码是一种基于概率的无损压缩方法。

信源符号和码字之间不存在一一对应关系。算术编码的解码过程是借助对信源符号的编码过程进行的。

算法

概率区间分配：首先，将每个符号分配到一个区间，区间的长度与符号出现的概率成正比。概率越高的符号对应的区间越大。
逐步缩小区间：从左到右依次处理消息中的每个符号，将当前的区间缩小到对应符号的区间。每处理一个符号，区间就变得更小。
输出最终编码：最终，编码结果是这个小区间中的某一个值（通常选择区间的中值），并将其转换为二进制数。

例

对b1b2b3b4编码：

b1出现的概率10%，b2的概率48%，......
在第一个符号b1对应的区间[0, 0.1]中，再按照b2的概率缩小范围，......
直到最后一个符号，图中是b4，区间是[0.0341,0.0366]，故任取改区间内的一个值，如可取取0345对应b1b2b3b4。
在解码时，算法会从这个数值开始，依次按照概率区间分割的顺序还原回原来的符号序列。每次解码都通过缩小区间范围，直到还原出最初编码时的完整符号序列。

算术编码的优点是可以达到接近信息熵的压缩效率，但其计算复杂度较高，尤其在长消息中，这使其计算资源消耗较大。算术编码比哈夫曼编码更适合精细压缩，尤其是在高压缩率和无损传输的多媒体文件中常用。

LZW编码（Lempel-Ziv-Welch)

原理：将定长码字分配给变长信源符号序列。无损。

算法

1）字典初始化，
2）扫描像素，
3）判断当前词是否是新单词，之后判断否有新单词出现？
4）字典更新

例

若正在被处理的像素值在字典中、且与后续的像素值构成新字符，那就直接输出；并从当前字符位置处开始记录与后续字符构成的新字符，若新，则加入字典，等待下一次若扫描到这个像素序列，就以连续序列的方式输出编码。

行程编码

行程编码是一种将连续重复的相同数据（如图像中的相同像素值）表示为该数据和重复次数的编码方法，用于压缩数据。特别适合二值图像！！！无损

算法

1）扫描像素，
2）记录（灰度，行程）对。

例

预测编码

预测编码（Predictive Coding)，就是根据“过去”的时刻的像素值，运用一种模型，预测当前的像素值，预测编码通常不直接对信号编码，而是对预测误差进行编码。当预测比较准确，误差较小时，即可达到编码压缩的目的。无损，用于减少相关性带来的冗余性。

原理：对图像的一个像素的离散幅度的真实值，利用其相邻像素的相关性，预测它的下一个像素的可能值，再求两者差，对这种具有预测性质的差值，量化，编码，就可以达到压缩的目的。

每行的最开始的几个像素无法预测，这些像素需要用其他方式编码，这是采用预测编码所需要的额外操作。

预测编码示意图：

例

预测 $eq?%5Chat%7Bf%7D$ ：如图中标注；对预测误差 Δ编码；

通过预测值 $eq?%5Chat%7Bf%7D$ 和预测误差 Δ 的累加，逐步还原出原始图像的像素值。

(块)变换编码

原理：图像数据经过正交变换后，其变换系数具有一定的相互独立性，（例如，对于FT傅里叶变换来说，频普系数大的变换系数均集中在低频部分，而高频部分的幅值均很小，因而可以对低频的变换系数量化、编码和传输，对高频部分不处理，这样可以达到图像压缩的目的。通常是有损编码。

变换编码的一般系统框图：

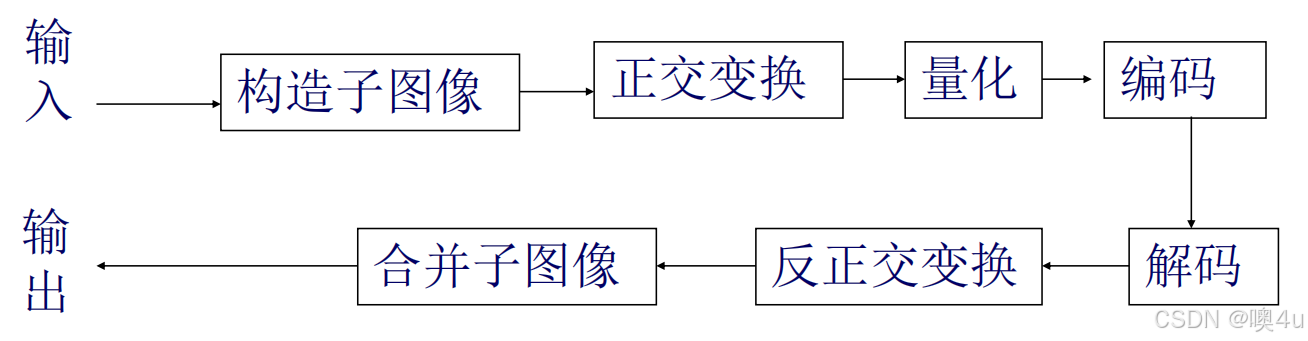
常见的变换编码方法包括：

离散傅里叶变换（DFT）：
- 将图像数据从空间域转换到频率域，便于去除高频部分。傅里叶变换主要用于频率分析，但直接应用在图像压缩中较少。
离散余弦变换（DCT）：
- 是最常用的变换编码方法之一，用于JPEG图像压缩。DCT可以有效地将图像的能量集中在低频区域，因此高频部分可以被较大程度地量化或舍弃，从而减少数据量。
离散小波变换（DWT）：
- 小波变换是一种多分辨率分析方法，将图像分解成不同的频带，用于JPEG 2000等标准。DWT相比DCT更适合处理图像中的突变和边缘信息，因此在图像压缩方面具有一定优势。
卡尔曼-洛伊夫变换（KLT）：
- 又称主成分分析（PCA），通过去除相关性来压缩数据，适合于统计相关性较强的数据，但计算复杂度较高，实际应用较少。
霍夫变换：
- 虽然霍夫变换主要用于形状检测，但在某些特定的图像处理中可以被用作变换编码方法，尤其是在边缘检测和形状识别中有一定的应用。