概率统计期末知识点复习

一、事件运算及概率

1. 事件及运算——文氏图及运算

2. 事件及运算公式

3. 古典概型公式

二、全概率公式、贝叶斯公式

1. 条件概率、乘法公式

2. 全概率公式、贝叶斯公式

三、一维随机变量

1. 离散型随机变量分布律、分布函数

2. 离散型随机变量函数的

3. 连续型随机变量的概率密度

4. 连续型随机变量的分布函数

5. 连续型随机变量函数的分布

四、五种重要分布

1. 其中泊松分布若X、Y相互独立满足以下性质

2. 其中指数分布的无记忆性

3. 其中正太分布的两条性质

4. 标准正太分布的概率密度

五、离散型——二维随机变量

1. 独立条件

2. 求P{X=__ | Y=__}概率

3. 边缘分布律

 1)a=1/6-1/8=1/24
 2)1/6*c=a=1/24
    c=1/4
 3)c+f=1/4+f=1
    f=3/4
 4)b=c-a-1/8=1/4-1/24-1/8=1/12
 5)1/12=c*h=1/4*h
    h=1/3
 6)e=h-b=1/3-1/12=1/4
 7)1/8=c*g=1/4*g
    g=1/2
 8)d=g-1/8=1/2-1/8=3/8

六、二维连续型随机变量

1. 联合、边缘、条件概率密度以及独立性

七、二维连续型函数的分布

1. Z=X+Y分布

2. Z=XY分布

3. Z=max{X,Y}分布

4. 两个分布函数

八、数学期望、方差、协方差

1. 一维随机变量的类型

2. 常用分布的数学期望和方差

3. 一维随机变量期望与方差

4. 二维随机变量期望与方差（离散型）

5. 二维随机变量期望与方差（连续型）

6. 协方差Cov(X,Y)

7. E(XY)=E(X)*E(Y)的性质

8. 切比雪夫不等式

九、大数定律、中心极限定理

1. 独立、同分布中心极限定理

2. 二项分布中心极限定理

十、抽样调查

1. 统计量不含任何未知参数

2. 三种常见分布

十一、参数估计

1. 矩估计

2. 最大似然估计

3. 无偏估计

十二、区间估计

1. 置信区间

2. 常考正太总体均值、方差的置信区间与单侧置信限

3. 置信区间求解

十三、假设检验

1. 常考的正太总体均值、方差的检验法

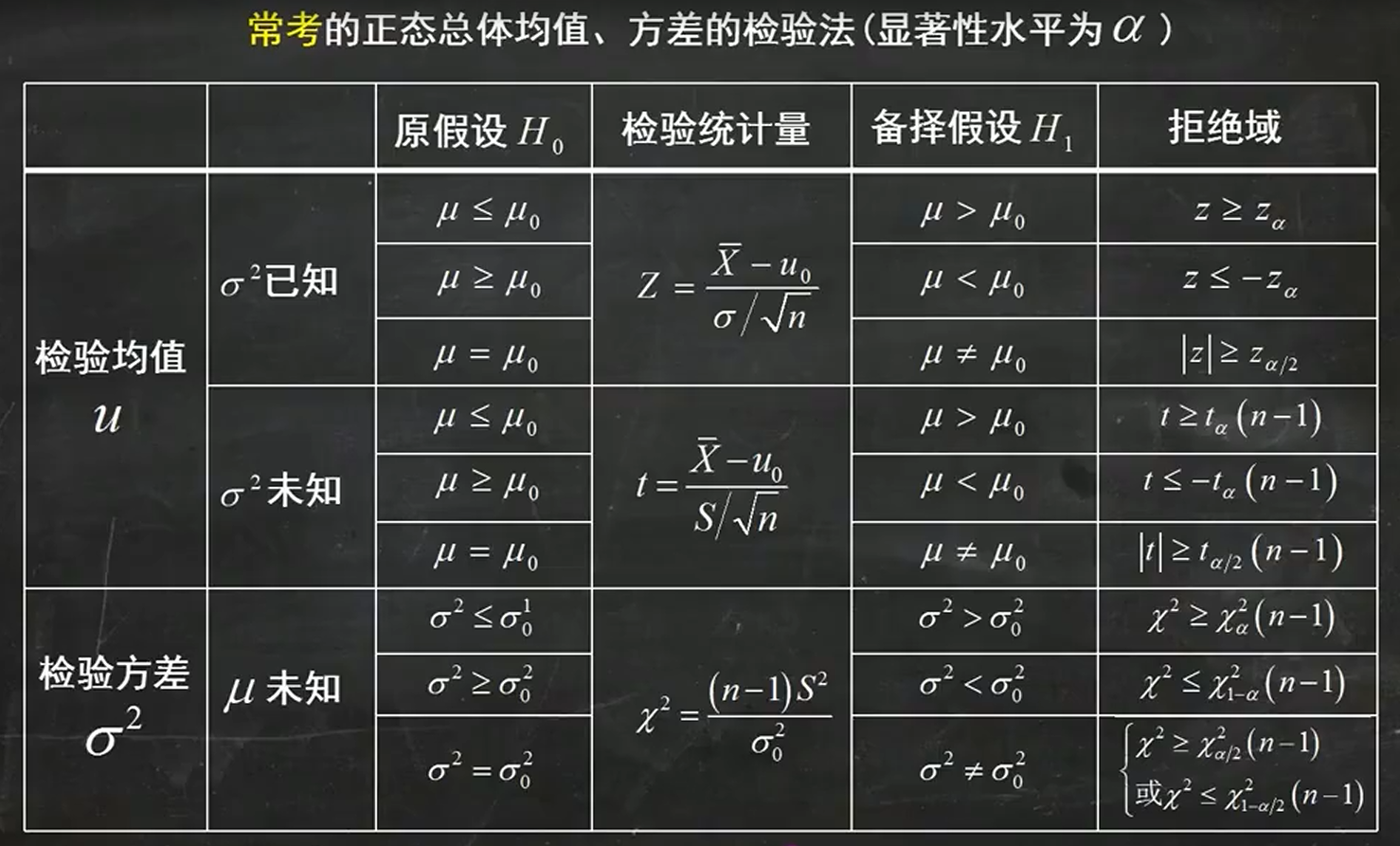
2. 假设检验步骤

3. Z检验

4. t检验

5. X^2检验

6. 两类错误