基于LSTM模型的城市轨道短时客流交通预测

最新推荐文章于 2025-05-05 14:07:50 发布

励志成为糕手

最新推荐文章于 2025-05-05 14:07:50 发布

阅读量730

点赞数 23

文章标签： lstm 人工智能机器学习长短时记忆网络

本文链接：https://blog.csdn.net/m0_74385041/article/details/147688968

版权

1.简述LSTM模型

对于LSTM模型的详细解析参考文章：LSTM模型全面解析-CSDN博客

简单的来说，LSTM（长短期记忆网络）是一种特殊的循环神经网络架构，专门用于解决传统RNN在处理长序列数据时的梯度消失问题。它通过引入单元（cell）和遗忘门、输入门、输出门三个门控机制，能够灵活地控制信息的存储、更新和输出。在每个时间步，遗忘门决定哪些信息需要遗忘，输入门负责更新单元状态，而输出门则控制单元状态中哪些信息需要输出到隐藏状态。这种结构使得LSTM能够有效地捕捉长距离依赖关系，广泛应用于自然语言处理、语音识别和时间序列预测等领域。

2.研究目标

轨道交通领域的数据集主要包含AFC刷卡数据、车站内视频监控数据、列车时刻表数据、相关的调研问卷数据等。本课题主要以基于卡数据的短时进展流预测为主，因此仅对AFC刷卡数据的开源数据集进行分析。

开源数据集包括已经经过预处理的北京地铁数据——北京地铁2016年2月29日-4月1日连续5周25个工作日的AFC刷卡数据，供给1.3亿条记录，数据跨度为05:00-23:00(18小时或1080min)，原始卡数据记录了卡号、进出站时间、进出站编号、进出站名称等信息。2016年3月，北京市共计17条运行路线和276座运营车站。处理后的AFC卡数据见附表。表格为276*1800（其中1800=25*72），其中276代表车站、25代表25个工作日，72代表每天72个采样点。In代表进站、out代表出站。数据预览如下：

3.数据预处理

选取两个csv数据包in_15min、out_15min(简称in，out数据包)，将两个数据矩阵进行转置(276*1800→1800*276)，后于首行插入递增数列，代表各个站点，每一列则分别代表该站点下不同测试点的客流数据。预览结果如下：

数据说明：由于机器学习按照每列抽取数据，而原数据包每列数学意义为276个站点同一个位置AFC刷卡数据。将该矩阵进行转置，则每列数据数学意义为276个站点中单个站点的1800测试点的数据，也就意味着该列为该站点的测试点数据汇总。同时在第一列插入自然数1,2,3,...,276，代表每个站点的数据。

数据的预处理中，发现in数据表中，以72个采样点为周期（每天为周期）。每天的72个采样点，第12/13采样点，达到顶峰，客流量最大，276个运营站点共大约22万客流量。第52-54采样点整体为第二顶峰，三点中，53点客流量最低。每天第一个采样点，客流量最小，276个运营站点客流量大约共1800。第27-42采样点客流量为第二波谷，较为平缓，276个运营站点客流量大致为四到五万。

out数据表中，以72个采样点为周期（每天为周期）。每天的72个采样点，第15-16采样点，达到顶峰，客流量最大，276个运营站点共大约23万客流量。第55-56采样点为第二顶峰，276个运营站点共大约14-16万客流量。每天第一个采样点，客流量最小，几乎为零。23-46采样点客流量为第二波谷，较为平缓。

出站折线图比进站相对推迟两三个采样点时间。

4.模型构建

4.1准备工作

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt

# 读取CSV数据
data = pd.read_csv('in_15min.csv')  # 替换为您的CSV文件路径

# CSV文件中有一个名为'1'的列，包含客流数据
data['1'] = data['1'].astype(float)
# 数据归一化
scaler = MinMaxScaler(feature_range=(0, 1))
data['1'] = scaler.fit_transform(data['1'].values.reshape(-1, 1))

首先是导入构建模型的架包和读取数据，我用的是torch进行模型构建。处理过后的数据第一行为自然数从1到276依次递增，对应每个每个站点的测试数据。之后，将数据进行归一化处理。

# 创建输入输出序列
def create_dataset(dataset, look_back=1):
    X, Y = [], []
    for i in range(len(dataset) - look_back - 1):
        a = dataset[i:(i + look_back), 0]
        X.append(a)
        Y.append(dataset[i + look_back, 0])
    return np.array(X), np.array(Y)

look_back = 1
X, Y = create_dataset(data['1'].values.reshape(-1, 1), look_back)
X = np.reshape(X, (X.shape[0], X.shape[1], 1))

# 划分训练集和测试集
train_size = int(len(X) * 0.8)
test_size = len(X) - train_size
X_train, X_test = X[0:train_size], X[train_size:len(X)]
Y_train, Y_test = Y[0:train_size], Y[train_size:len(Y)]

将时间序列数据转化为适合训练机器模型的输入输出格式，并划分训练集和测试集。

其中，创建输入输出列时：

np.reshape(X, (X.shape[0], X.shape[1], 1))：
- 将输入数据 X 的形状从 (n_samples, look_back) 转换为 (n_samples, look_back, 1)。
- 这是因为 LSTM 模型需要输入数据的形状为 (batch_size, sequence_length, features)，其中：
  - batch_size 是样本数量。
  - sequence_length 是序列长度（look_back）。
  - features 是特征数量（这里是 1，因为是单变量时间序列）。

另外，在划分训练集中，我们把训练集和测试集分别设置为总数据集的80%和20%，X_train, X_test是训练集的输入和输出，Y_train, Y_test是测试集的输入和输出。

4.2构建LSTM模型

# LSTM模型
class LSTMModel(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, output_size,dropout=0.2):
        super(LSTMModel, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)
        self.dropout = nn.Dropout(dropout)
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
        c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)
        out, _ = self.lstm(x, (h0, c0))
        out = self.fc(out[:, -1, :])
        return out

构建LSTM模型。首先初始化模型组件，其次定义前向传播方法——包括初始化隐藏状态和细胞状态h0和c0，LSTM层的前向传播，提取最后一个时间步的输出，最后将模型输出。

参数说明：
- input_size：输入特征的维度。对于单变量时间序列，input_size=1。
- hidden_size：LSTM 隐藏层的维度，决定了 LSTM 单元的复杂性。
- num_layers：LSTM 的层数（堆叠的 LSTM 层的数量）。
- output_size：模型输出的维度。对于单步预测任务，通常为 1。
- dropout：Dropout 比例，默认值为 0.2，用于防止过拟合。

4.3模型训练

# 实例化模型、定义损失函数和优化器
input_size = 1
hidden_size = 150
num_layers = 3
output_size = 1

model = LSTMModel(input_size, hidden_size, num_layers, output_size)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

# 训练模型
epochs = 150
for i in range(epochs):
    model.train()
    outputs = model(torch.from_numpy(X_train).float())
    optimizer.zero_grad()
    loss = criterion(outputs, torch.from_numpy(Y_train).float().unsqueeze(1))
    loss.backward()
    optimizer.step()
    if (i+1) % 10 == 0:
        print(f'Epoch [{i+1}/{epochs}], Loss: {loss.item():.4f}')

# 预测
model.eval()
predicted = model(torch.from_numpy(X_test).float())
predicted = predicted.detach().numpy()

# 反归一化
predicted = scaler.inverse_transform(predicted)
Y_test = scaler.inverse_transform(Y_test.reshape(-1, 1))

实例化模型中，对于不同站点的数据可以改变隐藏层，数据层的数值，同时可以适当调节学习率lr的值，以达到模型的最佳拟合。同时训练次数epochs避免太小导致模型欠拟合而效果不佳。

4.4模型评估

# 评估模型
mse = mean_squared_error(Y_test, predicted)
rmse = np.sqrt(mse)
r2 = r2_score(Y_test, predicted)
# 计算Adjusted R2
n = len(Y_test)  # 样本数量
p = 1  # 特征数量
adjusted_r2 = 1 - ((1 - r2) * (n - 1)) / (n - p - 1)

print(f'Test MSE: {mse}')
print(f'Test RMSE: {rmse}')
print(f'Test R2: {r2}')
print(f'Test Adjusted R2: {adjusted_r2}')

# 可视化预测结果
plt.figure(figsize=(10, 6))
plt.plot(Y_test, label='Actual')
plt.plot(predicted, label='Predicted')
plt.title('Passenger Flow Prediction')
plt.xlabel('Time')
plt.ylabel('Passenger Flow')
plt.legend()
plt.show()

在模型的评价指标中，采用MSE，RMSE，R^2和Adjusted_R^2评价拟合优度，以上是各个评价指标计算方法，最后输出各个指标数值，以及可视化预测结果。

五.结果评价

5.1评价指标

1.MSE即均方误差（Mean Squared Error），是一种用于衡量预测值与真实值之间差异的评标。它的计算方法是先求预测值与真实值之差的平方，再求这些平方值的平均数。MSE的值越小，说明预测模型的准确性越高。

$MSE=\frac{1}{m}\sum_{i=1}^{m}(y_t-\hat{y}_t)^2$

2.RMSE是均方根误差（Root Mean Squared Error）。它是MSE（均方误差）的平方根。

计算方式是先按照MSE的计算方法求出预测值与真实值差的平方的均值，然后再开平方。

其值越小代表模型预测的精准度越高。

$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{m}\sum_{i=1}^{m}(y_t-\hat{y}_t)^2}$

3.R2系数（决定系数）用于评估回归模型的拟合优度。R^{2}的值介于0到1之间，其值越高，表明模型的拟合效果越好，越能解释因变量的变化。

$R^2=1-\frac{\sum_i (y_i-\hat{y_i})^2}{\sum_i(y_i-\bar{y_i})^2}$

4.Adjusted R - squared（调整后的R^{2}）是对R^{2}的一种修正。在回归模型中，R^{2}会随着自变量个数的增加而增大，即便新增的自变量对模型并没有实质帮助。Adjusted R^{2}考虑了模型中自变量的数量。

$R^2_A=1-(1-R^2)=\frac{n-1}{n-p-1}$

其中，n是样本数量，p是自变量个数， $R^2$ 是决定系数

5.2运行结果预览

5.2.1 以站点“1”的刷卡数据为例，运行结果如下：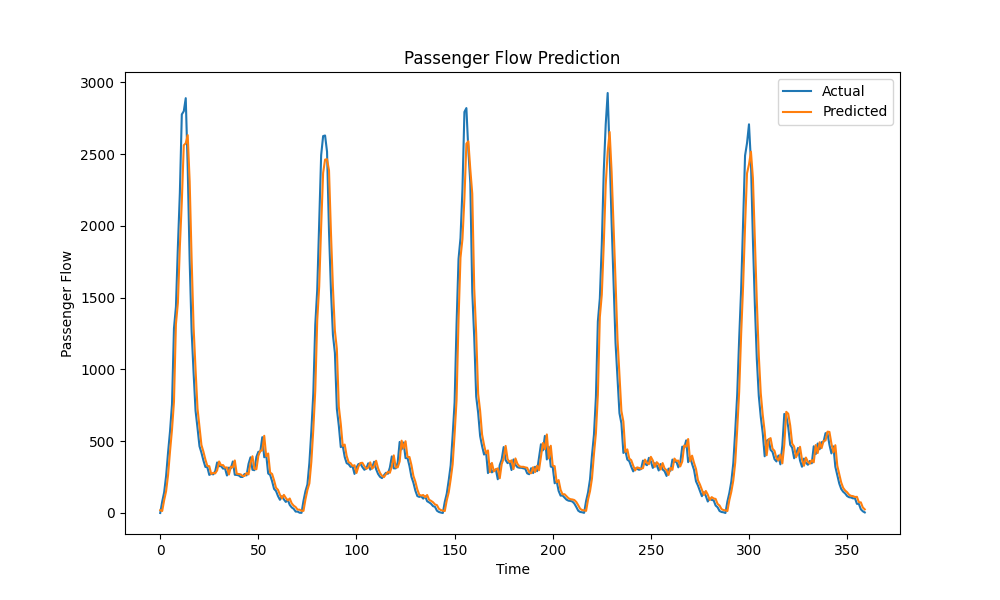

各评价指标数值如下：

Test MSE: 27375.132267413366
Test RMSE: 165.45432078798476
Test R2: 0.9350380784993495
Test Adjusted R2: 0.9348566206180627

可见，综合四个指标来看，在去除样本量的影响后R^2决定系数高达0.93，拟合效果较好。

5.2.2 以站点“12”的刷卡数据为例，运行结果如下：

(注：此时为刷卡数据达到顶峰时的数据，客流量最大)

可见，拟合效果依然很好，和站点“1”拟合水平相近。

5.2.2 以站点“276”的刷卡数据为例，运行结果如下：

(注：此时为刷卡数据的波谷，客流量最少)

Test MSE: 141.36506532422007
Test RMSE: 11.889704173116339
Test R2: 0.6148898924558139
Test Adjusted R2: 0.613814165898428

由四个评价指标综合来看，调整后的拟合系数R^2仅为0.61，拟合效果欠佳。

由于站点“276”数据量较小，考虑到数据可能存在过拟合的问题，此时应当谨慎调整隐藏层hidden_size、数据层num_layer以及学习率lr的数值，以及训练次数epochs，可以防止上述情况的发生。但经实验发现，处理的数据依然收效甚微，拟合误差有减小但不多。

Test MSE: 128.10909078193663
Test RMSE: 11.318528649163575
Test R2: 0.6510021368060956
Test Adjusted R2: 0.6500272824396323

5.3误差分析

在使用LSTM模型时，应当注意以下几个问题：

···超参数优化：学习率、批次大小、迭代次数等超参数的设置对模型性能有显著影响。动态调整学习率可以帮助模型更快、更稳健地收敛.

···梯度问题：LSTM能够缓解传统RNN中的梯度消失问题，但在某些情况下仍可能遇到梯度爆炸或消失的问题，可能需要梯度裁剪或特殊的激活函数来解决.

···计算复杂度：LSTM相比于标准RNN有更多的参数和更复杂的计算过程，导致更高的计算成本和更长的训练时间.

···过拟合风险：LSTM可能因为其强大的建模能力而容易过拟合，特别是在数据有限的情况下，需要采取正则化策略或使用更简洁的模型架构.

也就是说，对于每一组不同的站点数据，我们都可以找到不同的训练参数组使其拟合效果达到最佳。但LSTM也存在局限性：

···该模型计算复杂度高，内部结构相对复杂，参数多，导致高计算复杂度导致训练和推理速度较慢，尤其是在处理长序列或大规模数据集时。同时对硬件资源要求高，需要高性能的GPU或TPU来加速计算，否则难以在合理的时间内完成任务。

···难以解释的调试。例如站点“276”的数据预测。当模型出现错误或性能不佳时，调试和优化变得更加困难；LSTM模型的预测结果不准确，很难通过分析模型内部的门控机制来找到问题所在。即使调整各项参数，提升效果并不大。

···该模型对数据敏感性较高。LSTM的性能高度依赖于输入数据的质量和预处理方式。如果输入数据存在噪声、缺失值或不合理的归一化，模型的性能可能会大幅下降；同时，该模型数据的分布和特征工程也比较敏感。如果输入数据的特征没有很好地提取出来，模型可能无法有效学习到有用的模式。

由上述运行结果预览我们也可得知，在处理数据量稍大，数据复杂度高时拟合效果较好；但在站点数据平缓的拟合效果欠佳，此时如果还包含敏感数据，将大大降低拟合效果。因此应当适当结合其他机器学习的模型并行运用，对不同数据大小的站点实现最佳拟合。

六.总结

通过网盘分享的文件：城市轨道短时客流交通预测.zip
链接: https://pan.baidu.com/s/1HyTnjeGK-gqo7Oo4htRK0A 提取码: wlgd