六足机器人步态过程分析及控制

目录

前言

一、遇到的问题

二、运动过程

三、协调运动

四、步态控制

五、结语

---

前言

经过了几个STM32的小项目，积攒了一些项目经验，决定做一个六足机器人，购买完舵机和支架组装好机器人，随后就开始了项目。六足机器人可以使用D-H建立模型构建运动学坐标系，再正逆运动学解算腿部末端的位置与各个关节角度的关系式，也可以使用几何法来分析出关系式。网上很容易找到，就不赘述了，这里用C语言直接表示出来。

#include "stdio.h"
#include "math.h"

//六足机器人腿上的三根连轴 
#define L1 45
#define L2 73
#define L3 115


float get_angle1(float x,float y,float z)
{
	double angle;
	angle=atan2(y,x);
	return angle;  
}
/*   注释部分时利用几何法解算的 
float get_angle2(float x,float y,float z)
{
	float angle;
	float R = sqrt(pow(x, 2) + pow(y, 2));
	float Lr=sqrt(pow(z, 2) + pow((R - L1), 2));
	float ar = atan(-z / (R - L1));                                                                                                                                                                                                              
	float a1=acos((pow(L2, 2) + pow(Lr, 2) - pow(L3, 2)) / (2 * Lr * L2));

	angle=a1-ar;

	return angle;
}

float get_angle3(float x,float y,float z)
{
	float angle;
	float R = sqrt(pow(x, 2) + pow(y, 2));
	float Lr=sqrt(pow(z, 2) + pow((R - L1), 2));
	float a1=acos((pow(L2, 2) + pow(Lr, 2) - pow(L3, 2)) / (2 * Lr * L2));
	float a2=acos((pow(Lr, 2) + pow(L3, 2) - pow(L2, 2)) / (2 * Lr * L3));

	angle=-(a1 + a2);
	
	return angle;
}
*/

//该部分时逆运动学解算的 
float get_angle2(float x,float y,float z)
{
	float data= L1-sqrt(pow(x,2)+pow(y,2)) ; 
	float a = (pow(L2,2)-pow(L3,2)+pow(data,2)+pow(z,2) )/(2*L2*sqrt( pow(data,2) +pow(z,2)));
	float b = z/data;
	float angle = acos(a)-atan(b);
	return angle;
}


float get_angle3(float x,float y,float z)
{
	float data= L1-sqrt(pow(x,2)+pow(y,2)) ; 
	float a = (pow(L2,2)-pow(L3,2)+pow(data,2)+pow(z,2) )/(2*L2*sqrt( pow(data,2) +pow(z,2)));
	float b = (pow(L3,2)-pow(L2,2)+pow(data,2)+pow(z,2) )/(2*L3*sqrt( pow(data,2) +pow(z,2)));
	
	float angle=-acos(a)-acos(b);
	
	return angle;
}


//正运动学结算 
float get_x(float angle1,float angle2,float angle3)
{
	return cos(angle1)*( L1+L3*cos(angle2+angle3)+L2*cos(angle2) );
}

float get_y(float angle1,float angle2,float angle3)
{
	return sin(angle1)*(L1+L3*cos(angle2+angle3)+L2*cos(angle2));
}

float get_z(float angle1,float angle2,float angle3)
{
	return L3*sin(angle2+angle3)+L2*sin(angle2);
}

int main(void)
{
    float angle1,angle2,angle3;
	float x,y,z;
	
	//逆运动学解算 
	angle1=get_angle1(100,100,-80);
	angle2=get_angle2(100,100,-80);
	angle3=get_angle3(100,100,-80);

	printf("angle1:%f\r\n",angle1* (180.0 / M_PI));
 	printf("angle2:%f\r\n",angle2* (180.0 / M_PI));
	printf("angle3:%f\r\n",angle3* (180.0 / M_PI));
	
	//正运动学结算 
	x=get_x(angle1,angle2,angle3);
	y=get_y(angle1,angle2,angle3);	
	z=get_z(angle1,angle2,angle3);
	
	printf("x:%f\r\n",x);
 	printf("y:%f\r\n",y);
	printf("z:%f\r\n",z);
	
    return 0；
}

查找资料的时候在嘉立创开源广场看到了一位大佬做的六足，我的六足机器人的姿态和位置控制就看大佬的PDF写的，如果大家想做六足机器人，建议先看一下这位大佬写的PDF，再来看这篇文章。 链接：十二分感谢这位佬https://oshwhub.com/ryzee/Hexapod-robot

一、遇到的问题

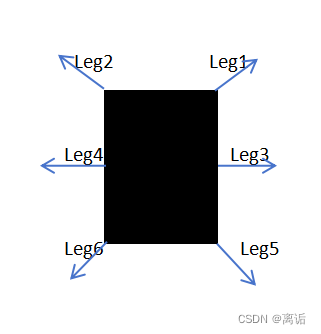
看完这位佬的PDF里面的全向移动，我知道了全向移动时六条腿的落脚点位置如何解算出来的了，但还不知道这个运动过程是如何完成的，还有让这六条腿协调运动以及步态控制，经过一些时间的思考，想出了一个解决办法，先上图，下面是我的六足机器人步态时序图。（随手画的，有些潦草，见谅）       

二、运动过程

黑色部分是抬腿在空中向前滑动至落脚点的时间，白色部分是在地面上向后滑动的时间   

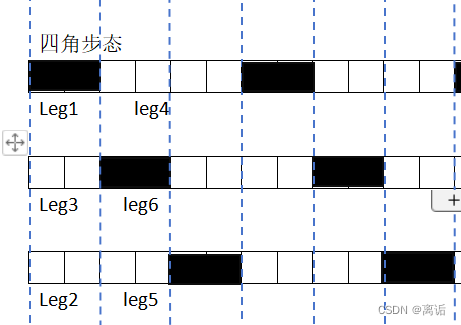
我认为控制这个步态应该从时间上入手，以黑色部分是抬腿在空中滑动至落脚点（这个运动过程我称为运动一）的时间，为一个时间节拍；白色部分是在地面上向后滑动（这个运动过程我称为运动二）的时间，跟据不同的步态分别为一个时间节拍，两个时间节拍和五个时间节拍。可以通过控制一个节拍的时间，来控制住机器人运动的快慢。

先解决从抬腿点移动至落腿点这个运动，如何使运动一的时间刚好为一个节拍呢，相信下面的公式大家都知道

                 

从X-Y平面上看，因为已经知道了落脚点的位置（），那么就将落脚点的位置减去抬脚点（，）的位置则就可以得到两点间的位移()，再将位移除以一个时间节拍就可以得到速度和了,开始运动时就定时器中断计时得到时间，将时间和速度带入公式当中就可以得到每时每刻的位置坐标（）,一个时间节拍结束后就可以精准达到落脚点的位置了。

                

解决了起点到达落脚点，但还没有将抬腿运动这个问题解决，这里我取了个巧（感觉有点随意了），我感觉抬腿的动作有点像函数在范围内波形，于是抬腿的函数就出来了。这里将抬腿的高度与需要移动的距离（）成正比，还需根据自己请况调整比例系数K的大小。 

 

OK，现在从起点抬腿在落点落腿这个运动解决了，那在地面上从划落点又划到起点怎么办呢，这个很好办，其实也跟上面的运动一样，只需将运动二的时间根据不同的步态调整为不同的时间，并且没有抬腿的动作，这个动作就完成了。

三、协调运动

在运动过程中，会积累一些误差导致运动不协调。为了解决这个问题，我在抬腿运动的起始点添加了一些条件判断。在开始抬腿动作时，会检查其他腿是否已经按照步态图的要求到达各自的位置。如果有腿尚未到位，会进行短暂等待（这段时间非常短，不会对整个运动过程产生影响）。一旦所有腿都到达位置，便会开始执行抬腿动作。

四、步态控制

在开始运动时会根据步态图将腿的状态放在时间线上不同位置，假设开始四角步态运动时，Leg1、Leg4在时间线上的起始处，Leg3、Leg6在时间线上的三分之二处（超前Leg1、Leg4一个时间节拍），Leg2、Leg5在时间线上的三分之一处（滞后Leg1、Leg4一个时间节拍），其他的步态以此类推。

六足机器人四角步态

在运动过程中切换步态（只是一些想法，这个还没开始弄，可能不太合适，仅供参考）有些要求，第一个要求就是所有腿在运动二的过程中速度要保持一致（运动一不需要管），这是推动机器人行走的一个过程，就像汽车行驶时前后轮子转速要一致的道理，所以切换步态的时候需要切换速度。第二个要求，抬腿的顺序发生改变，例如从三角步态切换至四角步态，在运行完一个节拍后切换步态，本该Leg2、Leg3 、Leg6进行运动一的，可是切换了步态就变成Leg3、Leg6进行运动一，Leg2人需要继续进行运动二。好了，现在将步态切换过程和问题分析出来了，剩下的就很好办了。

为了使切换的动作更加流畅，我认为收到切换步态的指令时，先将一个节拍的动作完成，就是在图中0、1、2、3、4、5、6号的时间位置切换步态。假设是在0到1的时间位置上收到的指令，在收到从三角步态切换到四角步态指令的那一刻将四角步态的速度计算出来，并在1号的时间位置将三角步态中运动二的速度换成四角步态中运动二的速度。Leg1、Leg4、Leg5完成运动一后，改变速度，接着Leg1、Leg4、Leg5开始运动二，Leg1、Leg4经过两个时间节拍后到达抬腿点，Leg5经过一个时间节拍后则开始运动一。Leg2、Leg3、Leg6完成运动二后，Leg3、Leg6开始运动一，经过一个时间节拍后到达落腿点，Leg2则继续保持运动二，经过一个时间节拍后，开始抬腿运动（这个需要计算出抬腿点的位置，因为在运动二中以四角步态多运动了一个节拍）。

五、结语

以上内容是在制作六足机器人遇到的一些问题和个人解决问题的方法措施，也希望大家能够通过这篇文章解决问题和疑惑。