支持向量机-SVM

支持向量机介绍

支持向量机（Support Vector Machine，SVM）是一种常用的机器学习算法，SVM可以用于线性和非线性分类问题，回归以及异常值检测
其基本原理是通过在特征空间中找到一个超平面，将不同类别的样本分开，并且使得离超平面最近的样本点到超平面的距离最大化。

以一个二维平面为例，判定边界是一个超平面（在本图中其实是一条线，但是可以将它想象为一个平面乃至更高维形式在二维平面的映射），它是由支持向量所确定的（支持向量是离判定边界最近的样本点，它们决定了判定边界的位置）。
间隔的正中就是判定边界，间隔距离体现了两类数据的差异大小
 

若严格地规定所有的样本点都不在“缓冲区”，都正确的在两边，称为硬间隔分类； 但是在一般情况下，不易实现，这里有两个问题：
第一，它只对线性可分的数据起作用。第二，有异常值的干扰。

为了避免这些问题，可使用软间隔分类：
在保持“缓冲区”尽可能大和避免间隔违规之间找到一个良好的平衡，在sklearn中的SVM类，可以使用超参数 C(惩罚系数），控制了模型的复杂度和容错能力。较小的C值会导致容错能力较高（即更宽的缓冲区），可能会产生更多的错误分类（即间隔违规）；较大的C值会导致容错能力较低，可能会产生更少的错误分类。

最大间隔与分类 

线性模型： 在样本空间中寻找一个超平面, 将不同类别的样本分开  

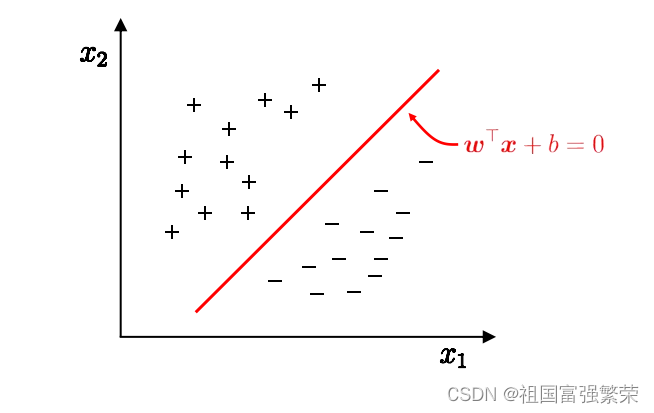
问题:  将训练样本分开的超平面可能有很多, 哪一个好呢

-应选择”正中间” , 容忍性好, 鲁棒性高, 泛化能力最强

超平面方程

对偶问题

给定一个目标函数 f : Rn→R，希望找到x∈Rn ，在满足约束条件g(x)=0的前提 下，使得f(x)有最小值。该约束优化问题记为：

对偶问题：不等式约束的KKT条件

将约束等式 g(x)=0 推广为不等式 g(x)≤0。这个约束优化问题可改

核函数

为什么要引入核函数呢？ 因为在SVM中，有时候很难找出一条线或一个超平面来分割数据集，这时候我们就需要升维（把无法线性分割的样本映射到高纬度空间，在高维空间实现分割）

核函数是特征转换函数，它可以将数据映射到高维特征空间中，从而更好地处理非线性关系。
核函数的作用是通过计算两个样本之间的相似度（内积）来替代显式地进行特征映射，从而避免了高维空间的计算开销。

在SVM中，核函数的选择非常重要，它决定了模型能够学习的函数空间。常见的核函数包括：

线性核函数（Linear Kernel）：最简单的核函数，它在原始特征空间中直接计算内积，适用于线性可分的情况。K(X,y) = (X^T) * y

多项式核函数（Polynomial Kernel）：通过多项式函数将数据映射到高维空间，可以处理一定程度的非线性关系。(可拟合出复杂的分割超平面，但可选参数太多，阶数高后计算困难，不稳定） K(X,y) = ( (X^T) * y + c ) ^ d , 其中 c 为常数，d 为多项式的阶数。

高斯核函数（Gaussian Kernel）：也称为径向基函数（Radial Basis Function，RBF），通过高斯分布将数据映射到无穷维的特征空间，可以处理更复杂的非线性关系。形式为 K(x,y) = exp( -|| x-y || ^2 / (2 σ ^2) ) 。
|| x - y || 表示向量 x 和 y 之间的欧氏距离，即它们各个维度差值的平方和的平方根。
σ 是高斯核函数的参数，控制了样本之间相似度的衰减速度。σ 越小，样本之间的相似度下降得越快；σ 越大，样本之间的相似度下降得越慢。

sigmoid核函数（Sigmoid Kernel）：通过sigmoid函数将数据映射到高维空间，适用于二分类问题。 σ(x) = 1 / (1 + exp(-x))

svm实现垃圾邮件分类

使用的数据集是ex6data3

# -*- coding: utf-8 -*-
"""
数据集：数据文件是ex6data3.mat
"""

import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from sklearn.svm import SVC  # 导入sklearn.svm的库

data = sio.loadmat('C:/Users/zhoutao/Desktop/ex6data3.mat')
print('data.keys():', data.keys())


X, y = data['X'], data['y']
Xval, yval = data['Xval'], data['yval']
print('X.shape, y.shape:', X.shape, y.shape)

# ---------------------------
# 画出数据的散点图来看看分布状况
def plot_data():
    plt.scatter(X[:, 0], X[:, 1], c=y.flatten(), cmap='jet')  #　cmap相当于是配色盘的意思，这次选择了jet这一套颜色。y.flatten()
    # 是将y拉伸成一列， 这样每一个X对应一个y,而y只有0，1两种，c是给数据点颜色,把0和1的数据点给出不同的颜色
    plt.xlabel('x1')
    plt.ylabel('y1')
    plt.show()

# plot_data()  # 调用函数，画出数据的散点图来看看分布状况
# ---------------------------

# ---------------------------
#　寻找准确率最高时候的最优参数C和gamma
Cvalues = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]  # 设置9个误差惩罚系数的候选值C
gammas = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]  # 设置9个高斯核的参数候选值gamma

best_score = 0  # 设置初始得分（即预测准确率）
best_params = (0, 0)  # 设置初始参数

for c in Cvalues:  # 遍历Cvalues中的候选值
    for gamma in gammas:  # 遍历gammas中的候选值
        svc = SVC(C=c, kernel='rbf', gamma=gamma)   # 将候选值一个一个代入SVC中
        svc.fit(X, y.flatten())
        score = svc.score(Xval, yval.flatten())   # 将svc后的结果代入验证集中，对Xval,yval进行验证，显示预测准确率，
        if score > best_score:  # 如果当前的分数score大于之前的历史最好分数best_score
            best_score = score  # 就将当前的分数score赋值成历史最好分数best_score
            best_params = (c, gamma)  # 并且把当前的参数c和gamma赋值成历史最好参数best_params
print('best_score, best_params:', best_score, best_params)
# ---------------------------

# ---------------------------
# 将最优参数代回去，得到最后的最优分类图像
svc2 = SVC(C=best_params[0], kernel='rbf', gamma=best_params[1])  # 其实C和gamma分别就是0.3和100
svc2.fit(X, y.flatten())

# 绘制决策边界
def plot_boundary(model):
    x_min, x_max = -0.6, 0.4  # 根据散点图看出数据点的x范围
    y_min, y_max = -0.7, 0.7 # 根据散点图看出数据点的y范围
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))  # np.meshgrid是画格子，这里xx和yy
    # 的shape为(500,500)，意思就是画个均匀的500*500的格子
    z = model.predict(np.c_[xx.flatten(), yy.flatten()])  # 将xx,和yy都从500*500降成一维，再用np.c_[]合并成shape为（250000，2）

    zz = z.reshape(xx.shape)  # (500,500)
    plt.contour(xx, yy, zz)   # 绘制等高线 # 这个等高线暂时不是很理解，这个画法摘自网络

plot_boundary(svc2)  # 调用边界函数画出决策边界
plot_data()    # 调用plot_data() 画出数据的散点图
plt.show()    # 上面两行只是调用，还没有画出来，有了这行之后是把上面两行画出的决策边界和散点图都显示到同一张图上来

小结

svm的优缺点

优点：

支持向量机算法可以解决小样本情况下的机器学习问题，简化了通常的分类和回归等问题。
由于采用核函数方法克服了维数灾难和非线性可分的问题，所以向高维空间映射时没有增加计算的复杂性。换句话说，由于支持向量计算法的最终决策函数只由少数的支持向量所确定，所以计算的复杂性取决于支持向量的数目，而不是样本空间的维数。
支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求，从而避免这些点对模型学习的影响。

缺点：

支持向量机算法对大规模训练样本难以实施。这是因为支持向量机算法借助二次规划求解支持向量，这其中会涉及m阶矩阵的计算，所以矩阵阶数很大时将耗费大量的机器内存和运算时间。
经典的支持向量机算法只给出了二分类的算法，而在数据挖掘的实际应用中，一般要解决多分类问题，但支持向量机对于多分类问题解决效果并不理想。
SVM算法效果与核函数的选择关系很大，往往需要尝试多种核函数，即使选择了效果比较好的高斯核函数，也要调参选择恰当的  参数。另一方面就是现在常用的SVM理论都是使用固定惩罚系数 ，但正负样本的两种错误造成的损失是不一样的。