关于膝关节运动损伤的数学模型

最新推荐文章于 2025-05-23 08:55:07 发布

maojian_369_NEUer

最新推荐文章于 2025-05-23 08:55:07 发布

阅读量1k

点赞数 27

分类专栏：数学建模文章标签：算法数学建模学习

本文链接：https://blog.csdn.net/maojian_369/article/details/145854336

版权

数学建模专栏收录该内容

1 篇文章

订阅专栏

关于膝关节运动损伤的数学模型

摘要

膝关节是人体最大、最复杂、最常受伤的关节之一。不当的运动极易对膝关节造成损伤，针对日常生活中平路正常步行、快步疾走、上楼、下楼等多种不同的情况，分析膝关节可能受到的损伤的问题，我基于多体动力学理论中拉格朗日方法，从系统的动能和势能角度入手，建立单侧下肢动力学模型，并使用curve_fit()拟合函数实现对模型进行求解。

最后，我校核了模型的计算结果，本文的模型贴合实际，能够依据该模型，给出给出膝关节保护的建议。

关键词: 膝关节保护拉格朗日方法下肢动力学模型

一、问题重述

1. 问题背景

膝关节是人体最大且最复杂的关节之一，容易受伤。由于不当运动，膝关节的关节囊和韧带在受到大力矩时容易损伤，尤其是像前交叉韧带（ACL）断裂这样的严重损伤，可能会改变膝关节的生物力学，甚至导致残疾。分析在不同日常活动如正常步行、快步疾走、上下楼梯中，膝关节主要组织的受力情况，以评估可能的损伤并提出保护膝关节的建议，已成为了人们关注的问题。

目前，随着人体工程学、多体动力学的发展，已经有很多学者对人体辅助装备面对的人体关节模型建立的问题进行了研究。相继提出了D-H 法运动学建模、拉格朗日法、牛顿欧拉法、Roberson-Wittenburg 法等建模方法来描述人体关节的运动状态。这有利于我在总结和分析已有的建模方法，设计出更为贴合问题需要的更为合理的模型。

1. 问题提出

问题一：建立人们运动过程中膝关节主要组织受力的数学模型，模型需要考虑日常生活中平路正常步行、快步疾走、上楼、下楼等多种不同的情况，分析膝关节可能受到的损伤，给出膝关节保护的建议。

二、问题分析

针对问题一：请查找相关论文和数据，建立人们运动过程中膝关节主要组织受力的数学模型，模型需要考虑日常生活中平路正常步行、快步疾走、上楼、下楼等多种不同的情况，分析膝关节可能受到的损伤，给出膝关节保护的建议。

我们需要将人体下肢和日常活动这两个方面进行化简以获取便于建立数学模型的几何模型。

2.1关于人体下肢的化简

在研究人体下肢运动时,骨骼常被简化为刚体连杆模型,根据所研究工况的不同,可以将模型简化为五肢段模型、七肢段模型和九肢段模型[1]。由于研究的对象是膝关节，所以，可以选择五肢段模型以减少计算量。五肢段模型包括髋骨,股骨和胫骨,不包括足部骨骼。因此，使用五肢段模型只是不能表征足部的运动状态，并不会影响膝关节的运动状态的表征，所以，在该问题中，选择五肢段模型化简人体下肢是合适的。

基于五肢段模型，可以进一步将人体下肢简化为刚体连杆模型。由于研究的运动过程以行走为主，根据对称关系，仅研究单侧下肢即可。

图2.1.1 五肢段模型图

2.2关于行走的简化

一个完整的步态周期以单侧腿足跟触地开始,到单侧腿第二次足跟触地结束,其中步态周期可以根据该足是否接触地面分为支撑相(Stance phase)和摆动相(Swing phase),支撑相可细分为双腿支撑(Single stance)与单腿支撑(Double stance)。

在描述人体各肢段以及各关节运动状态时,需要应用到人体坐标系。对于研究人体运动来说,行走,站起等运动常被简化为矢状面内的二维运动[2]。

三、模型假设与符号说明

3.1模型基本假设

（1）刚体假设：假设人体下肢各关节处的骨骼可以视为刚体，即关节处的骨骼不会发生形变。

（2）质量集中于质心：肢体的每个部分被简化为一个质点，其质量集中于各自的质心。

（3）运动不考虑肌肉和关节的变形：即忽略肌肉收缩和关节弯曲引起的形变。

（4）忽略内摩擦和空气阻力：研究过程中认为运动过程中不存在内摩擦和空气阻力的影响。

（5）力的作用简化解述：将肌肉的力量、地面反作用力等视为作用在质心或特定点。

3.2 符号说明

表1 符号说明

符号	含义	单位
m1	大腿质量	kg
m2	小腿质量	kg
q1	大腿质心距髋关节距离	m
q2	小腿质心距膝关节距离	m
l1	大腿长	m
l2	小腿长	m
θ1	大腿转角	rad
θ2	小腿转角	rad
K	动能	J
P	势能	J
F	力	N
M	力矩	N*m

四、模型建立与求解

4.1模型建立思路

多体动力学理论中，拉格朗日方法与牛顿—欧拉方法应用较为广泛[3]。其中拉格朗日方法因其对系统以的宏观角度，即以系统能量的角度来进行分析，在本模型中则主要为势能和动能两种能量。采用这种方法能更加直接反应系统工作原理并且著需要考虑运动前后的两种状态即可，运动过程则不必考虑。因此考虑以拉格朗日方法和单侧腿下肢为例,构建人体下肢动力学模型。

人体下肢坐标系，如图建立。

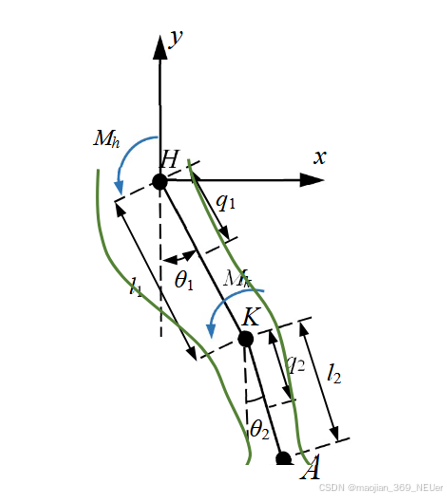
图4.1.1 人体下肢坐标系图

选取笛卡尔坐标系,H 为髋关节,K 为膝关节,A 为踝关节,大小腿的质量分别为 m1 和 m2,大腿质心距髋关节距离为 q1,小腿质心距膝关节距离为 q2,大腿长 l1,小腿长 l2。选取大腿与小腿的转角 θ1 和 θ2 做为变量。

4.2模型建立

拉格朗日函数 L 被定义为系统的动能 K 和位能 P 之差：

公式中 F 指力或力矩,q 为动能和位能的坐标,q̇ 为相应的加速度。

大腿质心的坐标：

x1=q1sinθ1

y1=q1cosθ1

大腿质心的合成速度：

小腿质心坐标：

$x_2=l_1sin\theta_1+q_2sin\left(\theta_2+\theta_1\right)$

$y_2=l_1cos\theta_1+q_2cos\left(\theta_2+\theta_1\right)$

小腿质心的合成速度：

$\begin{matrix}{\dot{x}}_2=l_1cos\theta_1{\dot{\theta}}_1+q_2cos\left(\theta_2+\theta_1\right)\left({\dot{\theta}}_2+{\dot{\theta}}_1\right)\\{\dot{y}}_2=-l_1sin\theta_1{\dot{\theta}}_1-q_2sin\left(\theta_2+\theta_1\right)\left({\dot{\theta}}_2+{\dot{\theta}}_1\right)\\\nu_2^2={\dot{x}}_2^2+{\dot{y}}_2^2=\left(l_1{\dot{\theta}}_1\right)^2+\left(q_2\left({\dot{\theta}}_2+{\dot{\theta}}_1\right)\right)^2+2l_1q_2\left({\dot{\theta}}_2+{\dot{\theta}}_1\right){\dot{\theta}}_1cos\theta_2\\\end{matrix}$

系统动能：

$E_{k1}=\frac{1}{2}m_1\nu_1^2=\frac{1}{2}m_1\left(q_1\dot{\theta_1}\right)^2$

$E_{k2}=\frac{1}{2}m_2\nu_2^2=\frac{1}{2}m_2\left(\left(l_1\dot{\theta_1}\right)^2+\left(q_2\left(\theta_2+\theta_1\right)\right)^2+2l_1q_2\left(\dot{\theta_2}+\dot{\theta_1}\right)\dot{\theta_1\cos{\theta_2}}\right)$

$E_k=E_{k1}+E_{k2}$

系统势能：采用竖直时质心的位置为 0 势能点。

$E_{p1}=m_1gq_1-m_1gq_1\cos{\theta_1}$

$E_{p2}=m_2g\left(l_1+q_2\right)-m_2g\left(l_1\cos{\theta_1}+q_2\cos{\left(\theta_2+\theta_1\right)}\right)$

$E_p=E_{p1}+E_{p2}$

代入拉格朗日方程中，经过计算可得：

髋关节 H 的力矩：

$\begin{matrix}\frac{\partial L}{\partial{\dot{\theta}}_1}=\left(m_1q_1^2+m_2l_1^2\right){\dot{\theta}}_1+m_2l_1q_2\left({\dot{\theta}}_2+2{\dot{\theta}}_1\right)cos\theta_2+m_2q_2^2\left({\dot{\theta}}_2+{\dot{\theta}}_1\right)\\\frac{\partial L}{\partial\theta_1}=-m_1gq_1sin\theta_1-m_2gl_1sin\theta_1-m_2gq_2sin\left(\theta_1+\theta_2\right)\\M_h=\frac{d}{dt}\frac{\partial L}{\partial{\dot{\theta}}_1}-\frac{\partial L}{\partial\theta_1}=\left(m_1q_1^2+m_2l_1^2+m_2q_2^2+2m_2l_1q_2cos\theta_2\right){\ddot{\theta}}_1\\+\left(m_2q_2^2+m_2l_1q_2\right){\ddot{\theta}}_2-2m_2l_1q_2\left({\dot{\theta}}_1{\dot{\theta}}_2\right)sin\theta_2\\-m_2l_1q_2\left({\dot{\theta}}_2^2\right)sin\theta_2+m_1gq_1sin\theta_1\\+m_2gl_1sin\theta_1+m_2gq_2sin\left(\theta_1+\theta_2\right)\\\end{matrix}$

膝关节的力矩:：

$\begin{matrix}&\frac{\partial L}{\partial{\dot{\theta}}_2}=m_2q_2^2\left({\dot{\theta}}_2+{\dot{\theta}}_1\right)+m_2l_1q_2{\dot{\theta}}_1cos\theta_2\\&\frac{\partial L}{\partial\theta_2}=-m_2gq_2sin\left(\theta_2+\theta_1\right)-m_2l_1q_2\left({\dot{\theta}}_2+{\dot{\theta}}_1\right){\dot{\theta}}_1sin\theta_2)\\&M_k=\frac{d}{dt}\frac{\partial L}{\partial{\dot{\theta}}_2}-\frac{\partial L}{\partial\theta_2}=\left(m_2q_2^2+2l_1q_2cos\theta_2\right){\ddot{\theta}}_1+m_2q_2^2{\ddot{\theta}}_2+\\&\left(-m_2l_1q_2sin\theta_2+m_2l_1q_2sin\theta_2\right)\left({\dot{\theta}}_1{\dot{\theta}}_2\right)+m_2l_1q_2\left({\dot{\theta}}_1^2\right)sin\theta_2+m_2gq_2sin\left(\theta_2+\theta_1\right)\\\end{matrix}$

4.3数据处理

在国际生物力学学会的生物力学数据资源索引网站中，里面包括了人体的运动数据、压力数据、肌肉骨骼模型数据等生物力学相关的数据，本文从这个网站中摘取下肢关节运动数据，并进行处理。

本文采用的是C3D TOOLS里面的Sample Gait Data中的gait-pig.c3d，可以看到里面包含的运动数据包括左髋、左膝、左踝、右髋、右膝、右踝等关节角度信息。根据模型需要，我们只需要其中的左膝关节、左踝关节的在行走时的角度信息。

数据经处理后，如下图所示。

图4.3.1 膝关节角度信息

图4.3.2 踝关节角度信息

不难直观看出，角度信息有明显的周期性，通过复合正弦函数拟合该曲线可以得到拟合函数。本文采用的拟合方法为 scipy.optimize.curve_fit()。

膝关节步态周期角度拟合函数为：

y1x=11.56sin0.13x-0.41-0.94sin0.31x-6.59-7.68sin0.26x+0.82-17.10

拟合效果如图所示：

图4.3.3 膝关节步态周期角度函数拟合效果图

踝关节步态周期角度拟合函数为：

y2x=-15.99sin0.14x-1.70+32407.14sin0.00x+11.03-20.44sin0.27x-2.03+32389.38

拟合效果如图所示：

图4.3.4 踝关节步态周期角度函数拟合效果图

由坐标系图可知，膝关节角度等于大腿转动角度，踝关节角度等于小腿转动角度。因此，模型中所需要的因变量θ1、θ2的函数表达式即为拟合出的函数y1、y2。

4.4模型求解

大腿与小腿的转角 θ1 和 θ2的函数后，我们可以对已有的模型进行求解。求解结果如下：

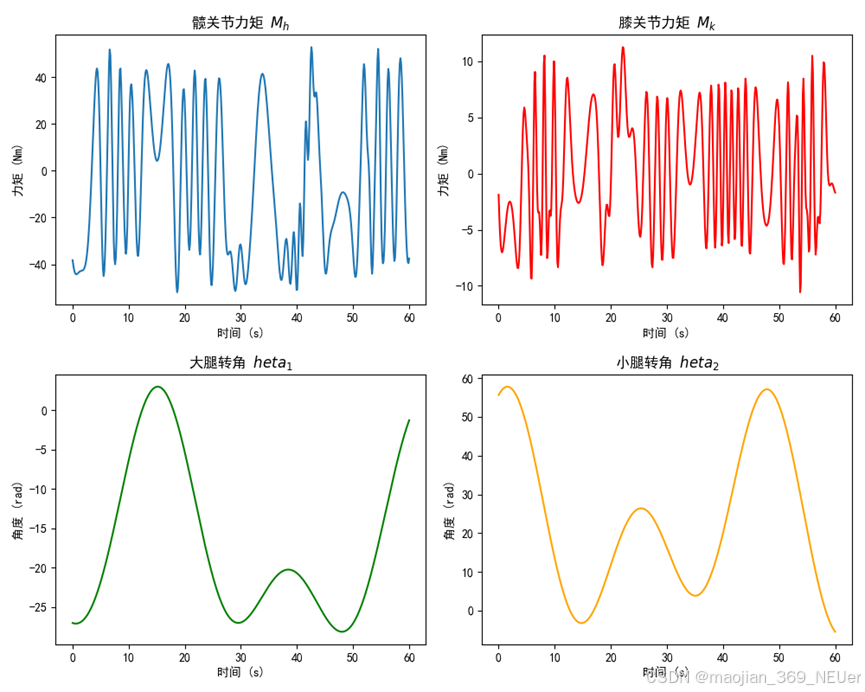
图4.4.1 关节力矩与下肢状态函数图

由图可知，当下肢处于过度伸直或是处于过度弯曲时，膝关节所承受的力矩将会达到极值，极易造成膝关节损伤。

基于以上研究，我提出建议：在行走时，膝关节应始终保持在一个合理范围内的角度，避免长时间过度伸展或弯曲。过度的膝关节伸展或弯曲可能导致膝关节内外侧的受力不均，增加损伤风险。

五、模型评价

模型给出的计算结果与实际情况大致吻合，可以为用于分析膝关节可能受到损伤的预估，并以此为依据给出膝关节保护的建议。

参考文献：

[1] 王达. 人体膝关节建模与有限元的数据分类方法研究[D/OL]. 沈阳工业大学, 2019.

[2] 周雅雯. 无动力膝关节助力外骨骼设计及分析研究[D/OL]. 西安理工大学, 2023.

[3] 赵琛. 行走过程中膝关节动力学特性分析[D/OL]. 吉林大学, 2023.

代码;

import numpy as np
import matplotlib.pyplot as plt

# 定义常数
m1 = 9.31  # 大腿质量 (kg)
m2 = 3.71  # 小腿质量 (kg)
g = 9.81  # 重力加速度 (m/s^2)
l1 = 0.496  # 大腿长度 (m)
l2 = 0.396  # 小腿长度 (m)
q1 = 0.25  # 大腿质心到髋关节的距离 (m)
q2 = 0.2  # 小腿质心到膝关节的距离 (m)

# 角度函数：大腿和小腿的角度是关于时间 t 的函数
def y1(t):
    return 11.56 * np.sin(0.13 * t - 0.41) - 0.94 * np.sin(0.31 * t - 6.59) - 7.68 * np.sin(0.26 * t + 0.82) - 17.10

def y2(t):
    return -15.99 * np.sin(0.14 * t - 1.70) + 32407.14 * np.sin(0.00 * t + 11.03) - 20.44 * np.sin(0.27 * t - 2.03) + 32389.38

# 定义髋关节力矩 M_h 和膝关节力矩 M_k 的计算函数
def M_h(theta1, theta2, theta1_dot, theta2_dot):
    term1 = (m1 * q1 ** 2 + m2 * l1 ** 2 + m2 * q2 ** 2 + 2 * m2 * l1 * q2 * np.cos(theta2)) * theta1_dot
    term2 = (m2 * q2 ** 2 + m2 * l1 * q2) * theta2_dot
    term3 = - 2 * m2 * l1 * q2 * theta1_dot * theta2_dot * np.sin(theta2)
    term4 = - m2 * l1 * q2 * theta2_dot ** 2 * np.sin(theta2)
    term5 = m1 * g * q1 * np.sin(theta1)
    term6 = m2 * g * l1 * np.sin(theta1)
    term7 = m2 * g * q2 * np.sin(theta1 + theta2)
    return term1 + term2 + term3 + term4 + term5 + term6 + term7


def M_k(theta1, theta2, theta1_dot, theta2_dot):
    term1 = (m2 * q2 ** 2 + 2 * l1 * q2 * np.cos(theta2)) * theta1_dot
    term2 = m2 * q2 ** 2 * theta2_dot
    term3 = (0) * theta1_dot * theta2_dot  # 该项为零
    term4 = m2 * l1 * q2 * theta1_dot ** 2 * np.sin(theta2)
    term5 = m2 * g * q2 * np.sin(theta1 + theta2)
    return term1 + term2 + term3 + term4 + term5


# 时间区间
t = np.linspace(20, 100, 500)  # 修改时间从0到60秒，共500个时间点

# 计算角度和角速度
theta1 = y1(t)  # 大腿角度
theta2 = y2(t)  # 小腿角度

# 计算角速度
theta1_dot = np.gradient(theta1, t)  # 计算大腿角速度
theta2_dot = np.gradient(theta2, t)  # 计算小腿角速度

# 计算髋关节力矩和膝关节力矩
M_h_values = [M_h(theta1[i], theta2[i], theta1_dot[i], theta2_dot[i])*0.25 for i in range(len(t))]
M_k_values = [M_k(theta1[i], theta2[i], theta1_dot[i], theta2_dot[i])*0.5 for i in range(len(t))]

# 绘制图像
fig, axs = plt.subplots(2, 2, figsize=(10, 8))
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 髋关节力矩图像
axs[0, 0].plot(t, M_h_values, label="髋关节力矩")
axs[0, 0].set_title("髋关节力矩 $M_h$")
axs[0, 0].set_xlabel("时间 (s)")
axs[0, 0].set_ylabel("力矩 (Nm)")

# 膝关节力矩图像
axs[0, 1].plot(t, M_k_values, label="膝关节力矩", color="red")
axs[0, 1].set_title("膝关节力矩 $M_k$")
axs[0, 1].set_xlabel("时间 (s)")
axs[0, 1].set_ylabel("力矩 (Nm)")

# 大腿转角图像
axs[1, 0].plot(t, theta1, label="大腿转角 $\theta_1$", color="green")
axs[1, 0].set_title("大腿转角 $\theta_1$")
axs[1, 0].set_xlabel("时间 (s)")
axs[1, 0].set_ylabel("角度 (rad)")

# 小腿转角图像
axs[1, 1].plot(t, theta2, label="小腿转角 $\theta_2$", color="orange")
axs[1, 1].set_title("小腿转角 $\theta_2$")
axs[1, 1].set_xlabel("时间 (s)")
axs[1, 1].set_ylabel("角度 (rad)")

# 调整布局
plt.tight_layout()
plt.show()

拟合函数代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 你提供的完整 y 数据
y_data = np.array([
    -26.24446, -26.52826, -26.2226, -25.4039, -24.12671, -22.2273, -19.84756,
    -16.97658, -13.70171, -10.16486, -6.62804, -3.35314, -0.65682, 1.28626,
    2.42153, 2.70532, 2.35601, 1.34084, -0.17651, -2.23972, -4.95786, -8.24362,
    -11.97695, -15.86312, -19.52007, -22.60935, -24.7926, -25.9934, -26.2663,
    -25.76411, -24.8035, -23.54815, -22.32551, -21.2994, -20.67716, -20.38244,
    -20.38244, -20.67716, -21.0811, -21.5723, -22.06355, -22.52202, -23.01322,
    -23.58091, -24.09395, -24.63975, -25.15282, -25.53487, -25.80777, -25.7314,
    -25.32746, -24.4651, -23.00234, -20.99376, -18.42845, -15.27368, -11.79141,
    -8.16721, -4.61946, -1.55198, 0.81686, 2.33418, 3.01101, 2.96733, 2.33419,
    1.11158, -0.72236, -3.16759, -6.23506, -9.84829, -13.73446, -17.53334,
    -20.88456, -23.5263, -25.18559, -26.02611, -25.9934, -25.44755, -24.58519,
    -23.63545, -22.80585, -22.32554, -22.11813, -22.20544, -22.58754, -23.1115,
    -23.74463, -24.45418, -25.05458, -25.65498, -26.16805, -26.53918, -26.74659,
    -26.87758, -26.92124, -26.83391, -26.63745, -26.25535, -25.65495, -24.80354,
    -23.49359, -21.72515, -19.49824, -16.82378, -13.66899, -10.31771, -7.02102,
    -3.87712, -1.34456, 0.51118, 1.58095, 1.94118, 1.67921, 0.92601
])

# 生成对应的 x 数据（假设从 0 到 len(y_data)-1）
x_data = np.arange(len(y_data))

# 定义复合正弦函数模型
def composite_sine_func(x, A1, B1, C1, A2, B2, C2, A3, B3, C3, D):
    return (A1 * np.sin(B1 * x + C1) +
            A2 * np.sin(B2 * x + C2) +
            A3 * np.sin(B3 * x + C3) +
            D)

# 使用 curve_fit 进行拟合，p0 是初始猜测值
params, covariance = curve_fit(composite_sine_func, x_data, y_data,
                               p0=[5, 0.1, 0, 5, 0.15, 0, 5, 0.2, 0, -25])

# 输出拟合结果
A1, B1, C1, A2, B2, C2, A3, B3, C3, D = params
print(f"拟合得到的参数:")
print(f"A1={A1:.2f}, B1={B1:.2f}, C1={C1:.2f}")
print(f"A2={A2:.2f}, B2={B2:.2f}, C2={C2:.2f}")
print(f"A3={A3:.2f}, B3={B3:.2f}, C3={C3:.2f}")
print(f"D={D:.2f}")

# 生成拟合的 y 值
y_fit = composite_sine_func(x_data, *params)

# 绘制原始数据和拟合曲线
plt.figure(figsize=(10, 6))
plt.scatter(x_data, y_data, label='原始数据', color='red')  # 绘制原始数据点
plt.plot(x_data, y_fit, label=f'拟合曲线', color='blue')  # 绘制拟合曲线
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 图表设置
plt.xlabel('x')
plt.ylabel('y')
plt.title('复合正弦函数周期数据拟合')
plt.legend()
plt.grid(True)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# 你提供的新的 y 数据
y_data = np.array([
    51.21538, 57.39376, 61.52012, 62.30592, 61.3236, 56.30198, 48.55144, 36.76198,
    22.46168, 7.13536, -5.37464, -13.14698, -16.33418, -15.0024, -10.33044, -5.22168,
    -0.96468, 0.76024, -0.26552, -2.7113, -5.964, -6.095, -2.90772, 3.81702, 12.54982,
    20.2567, 24.49204, 23.7937, 18.55362, 10.06078, 0.47654, -7.2741, -12.5792, -15.43916,
    -16.0287, -14.69692, -11.83714, -7.81966, -3.30048, 1.45894, 5.8254, 9.12212, 11.78566,
    13.7944, 16.23954, 18.90288, 22.87682, 26.85016, 31.71874, 35.95434, 39.81844, 41.2376,
    40.71352, 36.39096, 28.26932, 16.47986, 2.52864, -10.8328, -20.548, -24.82706, -23.99746,
    -20.04568, -14.17296, -8.91156, -5.96406, -6.0515, -9.1513, -13.08142, -15.24272, -12.57938,
    -5.50556, 4.4503, 13.8379, 18.75046, 18.72836, 13.09574, 4.0134, -6.40058, -15.39552,
    -20.19892, -21.48662, -19.4125, -15.00248, -9.50106, -3.93356, 1.45902, 5.62894, 9.82068,
    12.50624, 14.97322, 16.98196, 18.31348, 19.64558, 21.80702, 24.60124, 27.39604, 30.84526,
    34.51326, 36.7404, 37.56974, 36.4346, 32.11172, 24.88538, 14.51476, 1.80836, -11.61872,
    -22.55674, -28.7571, -29.73954, -26.52996, -20.50414, -14.56604, -9.74098, -8.12522
])

# 生成对应的 x 数据（假设从 0 到 len(y_data)-1）
x_data = np.arange(len(y_data))

# 定义复合正弦函数模型
def composite_sine_func(x, A1, B1, C1, A2, B2, C2, A3, B3, C3, D):
    return (A1 * np.sin(B1 * x + C1) +
            A2 * np.sin(B2 * x + C2) +
            A3 * np.sin(B3 * x + C3) +
            D)

# 使用 curve_fit 进行拟合，p0 是初始猜测值
params, covariance = curve_fit(composite_sine_func, x_data, y_data,
                               p0=[5, 0.1, 0, 5, 0.15, 0, 5, 0.2, 0, -25])

# 输出拟合结果
A1, B1, C1, A2, B2, C2, A3, B3, C3, D = params
print(f"拟合得到的参数:")
print(f"A1={A1:.2f}, B1={B1:.2f}, C1={C1:.2f}")
print(f"A2={A2:.2f}, B2={B2:.2f}, C2={C2:.2f}")
print(f"A3={A3:.2f}, B3={B3:.2f}, C3={C3:.2f}")
print(f"D={D:.2f}")

# 生成拟合的 y 值
y_fit = composite_sine_func(x_data, *params)

# 绘制原始数据和拟合曲线
plt.figure(figsize=(10, 6))
plt.scatter(x_data, y_data, label='原始数据', color='red')  # 绘制原始数据点
plt.plot(x_data, y_fit, label=f'拟合曲线', color='blue')  # 绘制拟合曲线
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体字
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# 图表设置
plt.xlabel('x')
plt.ylabel('y')
plt.title('复合正弦函数拟合')
plt.legend()
plt.grid(True)
plt.show()