统计假设测验------（四）方差分析（F测验、多重比较原理与方法）

最新推荐文章于 2024-09-06 16:21:08 发布

我不爱机器学习

最新推荐文章于 2024-09-06 16:21:08 发布

阅读量2.6w

点赞数 11

分类专栏：统计

本文链接：https://blog.csdn.net/mengjizhiyou/article/details/81946802

版权

统计专栏收录该内容

45 篇文章 28 订阅

订阅专栏

一、方差分析基本原理

1、方差分析（analysis of variance）:k（k>=3）个样本平均数假设测验方法。

与j无关的变量都看成常数，此时summation代表的是次数

方差分析基本步骤：

（1）将资料总变异的自由度和平方和分解为各变异原因的自由度和平方和，并算的其均方

（2）计算均方比，做出F测验，以明了各变异因素的重要程度

（3）对各平均数进行多重比较

2、F分布与F测验（比较两个事物变异大小）

在一个平均数为 $\mu$ 、方差为 $\sigma ^{2}$ 的正态总体中，随机抽取两个独立样本，分别求得其均方 $s_{1}^{2}$ 和 $s_{2}^{2}$ ，将其比值定义为F：

$F_{(v1,v2)}=$ $s_{1}^{2}$ / $s_{2}^{2}$

在给定的v1,v2下按上述方法从正态总体中进行一系列抽样，可得一系列的F值而作成一个F分布。

统计研究证明:

（1）F分布是具有平均数为1 ，取值空间为[0, $\infty$ ]一组曲线

（2）某一特定曲线的形状仅取决于参数v1和v2，v1=1或2时，曲线是严重倾斜成反向J曲线，v1>=3时，曲线转为偏态。

在方差体系中，F测验可用于检测某项变异因素的效用或方差是否真实存在。在计算F分布时，总是将要测验的那一项变异因素的均方作为分子，另一项变异（如试验误差项）的均方作为分母。这个问题与方差分析的模型和各项变异来源的期望均方有关。在此测验中，若分子的均方小于分母的均方，则F<1，不用查表即可确定P>0.05,接受无效假设，所以分子必须是大均方。

F测验需具备：

（1）变数y遵循正态分布N（ $\mu$ ， $\sigma ^{2}$ ）

（2） $s_{1}^{2}$ 和 $s_{2}^{2}$ 必须彼此独立

当资料不符合这些条件时，需做适当转换。

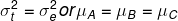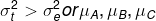对一组处理的重复试验数据经对总平方和与总自由度的分解估计出处理间均方与处理内均方（误差均方），通过F=MSt/MSe测验处理间所表示出的差异是否真实（比误差大），这一方法为方差分析法。所用统计假设H0： $\sigma _{t}^{2}=\sigma _{e}^{2} or \mu _{A}=\mu _{B}=\mu _{C}$ 或HA： $\sigma _{t}^{2}>\sigma _{e}^{2} or \mu _{A},\mu _{B},\mu _{C}$ 间存在差异（不一定三者都不等，可能部分不等）。

二、多重比较

对一组试验数据通过平方和与自由度的分解，将所估计的处理均方与误差均方作比较，由F测验推论处理间有显著差异，对有些试验方差分析已算告一段落，但对有些试验其目的不仅在于了解一组处理间总体上有无实质性差异，更在于了解哪些处理间存在真实差异，需进一步做处理平均数间的比较。一个试验中K个处理可能有K(K-1)/2个比较，这种比较是复式比较亦称多重比较（multiple comparisions）。

通过方差分析后进行平均数间的多重比较，不同于处理间两两单独比较。原因：

（1）误差由多个处理内的变异合并估计，自由度增大了，因而比较的精确度也增大了

（2）由于F测验显著，证实处理间总体上有真实差异后再做两两平均数的比较，不大会像单独比较时那样将个别偶然性的差异无误判为真实差异。在F测验基础上再做的平均数间多重比较称为Fisher氏保护下的多重比较（Fisher's protected multiple comparisons）。在无F测验保护时，处理间两两比较，每一比较的显著水平 $\alpha$ =0.05，若处理间总体上无差异，每一比较误判为有差异的概率为0.05，则6个比较中至少有一个被误判的概率为 $\alpha$ '=1- $0.95^{6}$ =0.2649;若处理数k=10，则 $\alpha$ '=1- $0.95^{45}$ =0.9006，因而尽管单个比较的显著水平为0.05，但从试验总体上 $\alpha$ ' （至少有一个误判的概率）是很大的，说明通过F测验做保护是非常必要的。

多重比较的方法：最小显著差数法，复极差法(q法)，Duncan氏新复极极差法。

方法一：最小显著差数法（least significant difference，LSD法），实质是t测验（成组）。

程序：在处理间的F测验为显著的前提下，计算出显著水平为 $\alpha$ 的最小显著差数 $LSD_{\alpha }$ ；任何两个平均数的差数（ $\bar{y}_{i}-\bar{y}_{j}$ ）,其绝对值 $\geq$ $LSD_{\alpha }$ ，即为在 $\alpha$ 水平上差异显著；反之在 $\alpha$ 水平上不显著。该法又称在F测验保护下的最小显著差数法。

方法二： q法（极差）

LSD法的t测验是根据两个样本平均数差数（k=2）的抽样分布提出的，但是一组处理（k>2）是同时抽取k个样本的结果。抽样理论指出k=2时与k>2，例如k=10时其随机极差是不同的，随着k的增大而增大，k=2时的t测验有可能夸大了k=10时最大与最小两个样本平均数差数的显著性。基于极差的抽样分布理论，Student-Newman-Keul提出了q测验或称负极差测验（SNK/NK测验）。

q测验方法是一组k个平均数由大到小排列后，根据所比较的两个处理平均数的差数是几个平均数间的极差分别确定最小显著极差 $LSD_{\alpha }$ 的值。

q测验根据极差抽样分布原理，其各个比较都保证同一个 $\alpha$ 显著水平，其尺度值构成为：

$LSD_{\alpha }$ = $\alpha _{(\alpha;df,p)}$ SE SE=sqrt(MSe/n)

式中2 $\leqslant$ p $\leqslant$ k,p是所有比较的平均数按大到小顺序排列所计算出的两极差范围内所包含的平均数个数（称为秩次距），SE是平均数的标准误。每一显著水平下有k-1个尺度值。平均数比较时，尺度值随秩次距的不同而异。

方法三：新复极差法

不同秩次距P下的最小显著极差变幅比较大，因此，D.B.Duncan提出新复极差法，又称最短显著极差法（shortest significant ranges,SSR）。与q法相似，其区别在于计算最小显著极差 $LSD_{\alpha }$ 时不是查q表而是查SSR表，所得最小显著极差值随k增大通常比q测验时减小。

$LSD_{\alpha }$ =SE* $SSR_{\alpha ,P}$

在不同秩次距p下，平均数间比较的显著水平按两两比较是 $\alpha$ ，但按p个秩次距则为保护水平 $\alpha$ '=1-(1- $\alpha$ )^(p-1)

二、多重比较结果的表示方法

（1）列梯形表法

（2）划线法

（3）标记字母法

首先将全部平均数从大到小依次排序，然后再最大的平均数标上字母a；并将该平均数与以下各平均数相比，凡相差不显著的都标上字母a,直至某一个与之相差显著的平均数则标以字母b（向下过程）；再以标有该字母b的最大平均数为标准，与以下未标记的平均数比，凡不显著的继续标以字母b，直至某一个与之相差显著的平均数则标以字母c。……如此重复下去，直至最小的一个平均数有了标记且与以上平均数进行了比较为止。各个平均数间，凡有一个相同标记字母的即为差异不显著，没有相同标记的即为差异显著。

三、多重比较方法的选择

参考原则：

（1）试验事先确定比较的标准，凡与对照相比较，或与预定要比较，或与预定要比较的对象比较，一般可选用最小显著差数法

（2）根据否定一个正确的H0与接受一个不正确的H0的相对重要性来决定。

四、方差分析的线性模型与期望均方

方差分析是建立在一定线性可加模型基础上。线性可加模型是指总体每一个变量可以按其变异的原因分解成若干个线性组成部分，是方差分析的理论依据。

五、单项分组资料的方差分析

单项分组资料是指观察值仅按一个方向分组的资料。

（1）组内观察值数目相等

（2）组内观察值数目不等

（3）组内又分亚组的单向分组资料的方差分析，

每组又分若干个亚组，每个亚组内又有若干个观察值，则为组内分亚组的单项分组资料，或称系统分组资料。系统分组并仅限于组内分亚组，亚组内还可分小组，小组内还可分亚组，……，如此一环套一环地分下去---巢式试验。