树

树的定义：
树(Tree)是n(n≥0)个相同类型的数据元素的有限集合。树中的数据元素叫结点(Node)。
n=0的树称为空树(Empty Tree)。

对于n＞0的任意非空树T有：
（1）有且仅有一个特殊的结点称为树的根(Root)结点，根没有前驱结点；
（2）若n＞1，则除根结点外，其余结点被分成了m(m＞0)个互不相交的集合T1，T2，…，Tm，其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1，T2，…，Tm称为这棵树的子树(Subtree)。
树的形式定义为：树(Tree)简记为T，是一个二元组，
T = (D, R)
其中：D是结点的有限集合；
R是结点之间关系的有限集合。

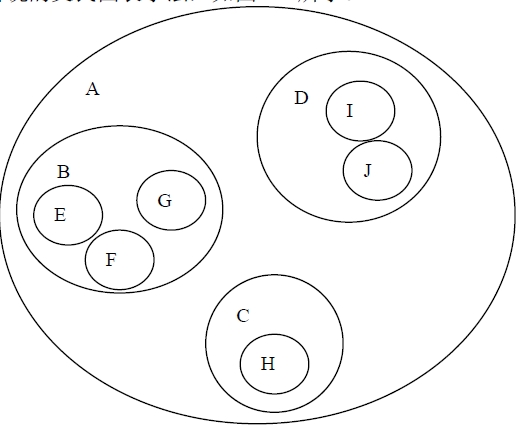
一棵具有10个结点的树，即T={A,B,C,D,E,F,G,H,I,J}。结点A是树T的根结点，根结点A没有前驱结点。除A之外的其余结点分成了三个互不相交的集合：T1={B,E,F,G}，T2={C,H}，T3={ D,I,J}，分别形成了三棵子树，B、C和D分别成为这三棵子树的根结点，因为这三个结点分别在这三棵子树中没有前驱结点。

树具有下面两个特点：
（1）树的根结点没有前驱结点，除根结点之外的所有结点有且只有一个前驱结点。
（2）树中的所有结点都可以有零个或多个后继结点。
实际上，第（1）个特点表示的就是树形结构的“一对多关系”中的“一”，第（2）特点表示的是“多”。
树的相关术语有以下一些：
1、结点(Node)：表示树中的数据元素，由数据项和数据元素之间的关系组成。在图5.1中，共有10个结点。
2、结点的度(Degree of Node)：结点所拥有的子树的个数，在图中，结点A的度为3。
3、树的度(Degree of Tree)：树中各结点度的最大值。在图中，树的度为3。
4、叶子结点(Leaf Node)：度为0的结点，也叫终端结点。在图中，结点E、F、G、H、I、J都是叶子结点。
5、分支结点(Branch Node)：度不为0的结点，也叫非终端结点或内部结点。在图中，结点A、B、C、D是分支结点。
6、孩子(Child)：结点子树的根。在图中，结点B、C、D是结点A的孩子。
7、双亲(Parent)：结点的上层结点叫该结点的双亲。在图中，结点B、C、D的双亲是结点A。
8、祖先(Ancestor)：从根到该结点所经分支上的所有结点。在图中，结点E的祖先是A和B。
9、子孙(Descendant)：以某结点为根的子树中的任一结点。在图中，除A之外的所有结点都是A的子孙。
10、兄弟(Brother)：同一双亲的孩子。在图5.1中，结点B、C、D互为兄弟。
11、结点的层次(Level of Node)：从根结点到树中某结点所经路径上的分支数称为该结点的层次。根结点的层次规定为1，其余结点的层次等于其双亲结点的层次加1。A B C D E F G H I J A C D H I J （a） （b） （c）
12、堂兄弟(Sibling)：同一层的双亲不同的结点。在图中，G和H互为堂兄弟。
13、树的深度(Depth of Tree)：树中结点的最大层次数。在图中，树的深度为3。
14、无序树(Unordered Tree)：树中任意一个结点的各孩子结点之间的次序构成无关紧要的树。通常树指无序树。
15、有序树(Ordered Tree)：树中任意一个结点的各孩子结点有严格排列次序的树。二叉树是有序树，因为二叉树中每个孩子结点都确切定义为是该结点的左孩子结点还是右孩子结点。
16、森林(Forest)：m(m≥0)棵树的集合。自然界中的树和森林的概念差别很大，但在数据结构中树和森林的概念差别很小。从定义可知，一棵树有根结点和m个子树构成，若把树的根结点删除，则树变成了包含m棵树的森林。当然，根据定义，一棵树也可以称为森林。

树的逻辑表示
树的逻辑表示方法很多，这里只讲几种常见的表示方法。
1、直观表示法
它象日常生活中的树木一样。整个图就象一棵倒立的树，从根结点出发不断扩展，根结点在最上层，叶子结点在最下面.
2、凹入表示法
每个结点对应一个矩形，所有结点的矩形都右对齐，根结点用最长的矩形表示，同一层的结点的矩形长度相同，层次越高，矩形长度越短。

3、广义表表示法
用广义表的形式表示根结点排在最前面，用一对圆括号把它的子树结点括起来，子树结点用逗号隔开。图5.1的树的广义表表示如下：
（A（B（E，F，G），C（H），D（I，J）））
4 嵌套表示法
类似数学中所说的文氏图表示法，

树的基本操作
1、Root()：求树的根结点，如果树非空，返回根结点，否则返回空；
2、Parent(t)：求结点t的双亲结点。如果t的双亲结点存在，返回双亲结点，否则返回空；
3、Child(t,i)：求结点t的第i个子结点。如果存在，返回第i个子结点，否则返回空；
4、RightSibling(t)：求结点t第一个右边兄弟结点。如果存在，返回第一个右边兄弟结点，否则返回空；
5、Insert(s,t,i)：把树s插入到树中作为结点t的第i棵子树。成功返回true，否则返回false；
6、Delete(t,i)：删除结点t的第i棵子树。成功返回第i棵子树的根结点，否则返回空；
7、Traverse(TraverseType)：按某种方式遍历树；
8、Clear()：清空树；
9、IsEmpty()：判断树是否为空树。如果是空树，返回true，否则返回false；
10、GetDepth()：求树的深度。如果树不为空，返回树的层次，否则返回0。

二叉树的定义
二叉树(Binary Tree)是n(n≥0)个相同类型的结点的有限集合。n=0的二叉树称为空二叉树(Empty Binary Tree)；对于n＞0的任意非空二叉树有：
（1）有且仅有一个特殊的结点称为二叉树的根(Root)结点，根没有前驱结点；
（2）若n＞1，则除根结点外，其余结点被分成了2个互不相交的集合TL，TR，而TL、TR本身又是一棵二叉树，分别称为这棵二叉树的左子树(Left Subtree)和右子树(Right Subtree)。
二叉树的形式定义为：二叉树(Binary Tree)简记为BT，是一个二元组，
BT = (D, R)
其中：D是结点的有限集合；
R是结点之间关系的有限集合。
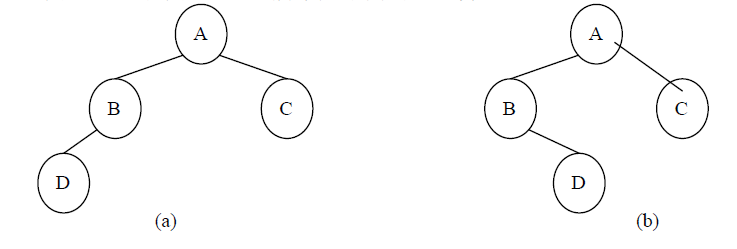
由树的定义可知，二叉树是另外一种树形结构，并且是有序树，它的左子树和右子树有严格的次序,若将其左、右子树颠倒，就成为另外一棵不同的二叉树。

下面介绍两种特殊的二叉树。
（1）满二叉树(Full Binary Tree)：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。
由定义可知，对于深度为k的满二叉树的结点个数为2k-1。
（2）完全二叉树(Complete Binary Tree)：深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k，有n个结点的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树。