决策树—ID3

决策树—ID3

1. 基本概念
   决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

2. 问题：
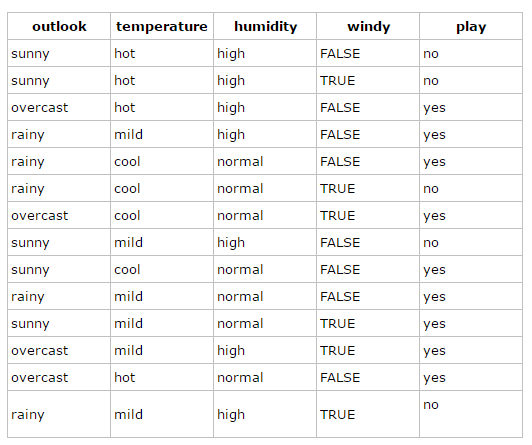
   14天的气象数据(指标包括outlook，temperature，humidity，windy)，并已知这些天气是否打球(play)。如果给出新一天的气象指标数据:sunny,cool,high,TRUE，判断一下会不会去打球。
   

3. 计算公式(信息熵)
   以什么标准来确定分支呢，比如说我们是以outlook还是以temperature来做为第一个分类的标准呢？这里用到了信息熵。熵是不确定性/无序性的度量指标，一个系统越是有序，信息熵就越低，反之一个系统越是混乱，它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。

一个随机变量X的取值为X={x1,x2,…xn}，每一个取到的概率是{p1,p2,…pn}，那么X的熵定义为：

$$H\left( X \right) = - \sum\limits_{i = 1}^n {p_i \log _2 p_i }$$
意思是一个变量的变化情况可能越多，那么它携带的信息量就越大。
信息增益是针对特征而言的就是由于使用这个属性分割样例而导致的期望熵降低，公式是：

Gain(S,A)=E(S)−∑v∈values(A)|Sv|S