本章介绍正演的基础知识. 仅供内部培训. 持续修改中.
2.1 弦线波动 (横波) 基本原理
波动方程是正演的基础. 最简单的模型是在一根弦上的波动.
在平面直角坐标系中, 令
X
X
X 轴上有一根起始于原点的弦. 通过在原点对其施加横向的力, 使得其发生横震动.
t
t
t 时刻在横坐标
x
x
x 处的振幅 (可以为负值) 记为
u
(
x
,
t
)
u(x, t)
u(x,t). 具体假设如下:
- 横震动. 在 Y Y Y 轴的偏移;
- 微小震动. 满足 u ( x + Δ x , t ) − u ( x , t ) ≪ Δ x u(x + \Delta x, t) - u(x, t) \ll \Delta x u(x+Δx,t)−u(x,t)≪Δx;
- 弦是柔软的. 张力沿着切线方向, 想像抖动一根大绳/皮鞭;
- 弦是均匀的. 密度均匀为 ρ \rho ρ.
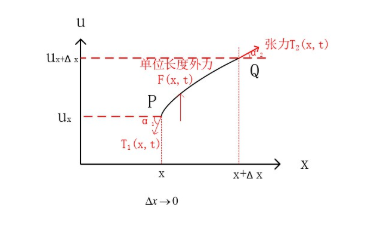
{
T
2
cos
α
2
−
T
1
cos
α
1
=
0
T
2
sin
α
2
−
T
1
sin
α
1
+
F
d
x
=
ρ
d
x
∂
2
u
(
x
,
t
)
∂
t
2
(2.1)
\begin{cases}T_2 \cos \alpha_2 - T_1 \cos \alpha_1 = 0\\ T_2 \sin \alpha_2 - T_1 \sin \alpha_1 + F \mathrm{d}x = \rho \mathrm{d}x \frac{\partial^2 u(x, t)}{\partial t^2}\end{cases} \tag{2.1}
{T2cosα2−T1cosα1=0T2sinα2−T1sinα1+Fdx=ρdx∂t2∂2u(x,t)(2.1)
其中, 第一个式子表示横向的拉力与张力, 因为没有横向移动.
第二个式子的依据是牛顿第二定律
F
=
m
a
F = ma
F=ma, 左式是三个力的合力,
F
d
x
F \mathrm{d}x
Fdx 中的
F
F
F 是单位长度的外力, 如重力,
d
x
\mathrm{d}x
dx 为该段弦的长度. 右式的
ρ
d
x
\rho \mathrm{d}x
ρdx 是质量, 二阶偏导为加速度.
由于是微小振动,
α
1
\alpha_1
α1 与
α
2
\alpha_2
α2 都接近
0
0
0, 因此有
{
cos
α
1
≈
1
;
cos
α
2
≈
1
;
sin
α
1
≈
tan
α
1
=
u
(
x
+
Δ
x
,
t
)
−
u
(
x
,
t
)
Δ
x
=
∂
u
(
x
,
t
)
∂
x
;
sin
α
2
≈
tan
α
2
=
∂
u
(
x
+
Δ
x
,
t
)
∂
x
.
\begin{cases} \cos \alpha_1 \approx 1;\\ \cos \alpha_2 \approx 1;\\ \sin \alpha_1 \approx \tan \alpha_1 = \frac{u(x + \Delta x, t) - u(x, t)}{\Delta x} = \frac{\partial u(x, t)}{\partial x};\\ \sin \alpha_2 \approx \tan \alpha_2 = \frac{\partial u(x + \Delta x, t)}{\partial x}. \end{cases}
⎩
⎨
⎧cosα1≈1;cosα2≈1;sinα1≈tanα1=Δxu(x+Δx,t)−u(x,t)=∂x∂u(x,t);sinα2≈tanα2=∂x∂u(x+Δx,t).
其中第三个式子表示右边质点的位置将要成为左边质点的下是一个位置,
利用牛顿第二定律
F
=
m
a
F = ma
F=ma 和上述假设条件可以推出一维非齐次波动方程的解:
∂
2
u
(
x
,
t
)
∂
t
2
=
c
2
∂
2
u
(
x
,
t
)
∂
x
2
+
f
(
x
,
t
)
(2.1)
\frac{\partial^2 u(x, t)}{\partial t^2} = c^2 \frac{\partial^2 u(x, t)}{\partial x^2} + f(x, t) \tag{2.1}
∂t2∂2u(x,t)=c2∂x2∂2u(x,t)+f(x,t)(2.1)
其中
c
2
=
T
/
ρ
c^2 = T / \rho
c2=T/ρ,
f
(
x
,
t
)
=
F
(
x
,
t
)
/
ρ
f(x, t) = F(x, t) / \rho
f(x,t)=F(x,t)/ρ, 左式的物理意义是瞬时加速度
a
a
a, 右式第一项的物理意义是 单位质量所受的力
F
F
F,
c
c
c 的物理意义是速度.
进一步忽略重力
F
(
x
,
t
)
F(x, t)
F(x,t) 的作用, 可以推出一维齐次波动方程的解:
∂
2
u
(
x
,
t
)
∂
x
2
=
1
c
2
∂
2
u
(
x
,
t
)
∂
t
2
(2.2)
\frac{\partial^2 u(x, t)}{\partial x^2} = \frac{1}{c^2} \frac{\partial^2 u(x, t)}{\partial t^2} \tag{2.2}
∂x2∂2u(x,t)=c21∂t2∂2u(x,t)(2.2)
更多内容参见: 弦线上的波动方程推导
中学物理已经教了横波的知识, 这里有个动画可以参考: 借助水波,理解横波
2.2 弦线纵波基本原理
u
(
t
,
t
)
=
c
∇
2
u
u(t, t) = c \nabla^2 u
u(t,t)=c∇2u
∂
u
t
∂
t
=
c
∇
2
u
\frac{\partial u_t}{\partial t} = c \nabla^2 u
∂t∂ut=c∇2u
2.3 阻尼波动基本原理
阻尼标量波动方程
p
u
≡
∇
2
u
(
x
,
t
)
−
h
(
x
)
∂
2
u
(
x
,
t
)
∂
t
2
−
g
(
x
)
∂
u
(
x
,
t
)
∂
t
=
f
(
x
,
t
)
(2.1)
pu \equiv \nabla^2 u(x, t) - h(x) \frac{\partial^2 u(x, t)}{\partial t^2} - g(x) \frac{\partial u(x, t)}{\partial t} = f(x, t) \tag{2.1}
pu≡∇2u(x,t)−h(x)∂t2∂2u(x,t)−g(x)∂t∂u(x,t)=f(x,t)(2.1)
式中,
- u u u 表示地球物理场的一种, 如声场, 电磁场的某一分量等;
- f ( x , t ) f(x, t) f(x,t) 为源函数;
- x x x 为空间的一个点, 见符号表;
- 系数 h h h 和 g g g 对不同场有不同的物理意义, 见表 4.1.
| 方法 | 物理场 | h h h | g g g |
|---|---|---|---|
| 地震 | 声压或位移分量 | 1 / c 2 1/c^2 1/c2 | 2 a / c 2a/c 2a/c |
| 电子磁法 | 磁场分量或电场分量 | μ ε \mu \varepsilon με | μ σ \mu \sigma μσ |
| 地质雷达 | 电场分量 | μ ε \mu \varepsilon με | 0 0 0 |
| 低频电磁法 | 电磁场分量 | 0 0 0 | μ σ \mu \sigma μσ |
| 传导类电法, 重力, 磁法 | 位场 | 0 0 0 | 0 0 0 |
c c c 为波数, α \alpha α 为波场衰减系数, μ \mu μ 为磁导率, ε \varepsilon ε 为介电系数, σ \sigma σ 为电导率.
2.4 正演模型
∇
2
p
(
r
,
t
)
−
1
v
(
r
)
2
∂
2
p
(
r
,
t
)
∂
t
2
=
s
(
r
,
t
)
(1)
\nabla^2 p(\mathbf{r}, t) - \frac{1}{v(\mathbf{r})^2} \frac{\partial^2 p(\mathbf{r}, t)}{\partial t^2} = s(\mathbf{r}, t) \tag{1}
∇2p(r,t)−v(r)21∂t2∂2p(r,t)=s(r,t)(1)
其中
p
(
r
,
t
)
p(\mathbf{r}, t)
p(r,t) 是在
t
t
t 时刻, 位置
r
\mathbf{r}
r 的压力波场,
v
(
r
)
v(\mathbf{r})
v(r) 是速度图,
s
(
r
,
t
)
s(\mathbf{r}, t)
s(r,t) 为源项.
正演过程为
p
~
=
f
(
v
^
)
(2)
\tilde{\mathbf{p}} = f(\hat{\mathbf{v}}) \tag{2}
p~=f(v^)(2)
2.5 有限差分法
标准的有限差分法
∂
2
p
(
r
,
t
)
∂
t
2
≈
1
(
Δ
t
)
2
(
p
r
t
+
1
−
2
p
r
t
+
p
r
t
−
1
)
+
O
(
(
Δ
t
)
2
)
(5)
\frac{\partial^2 p(\mathbf{r}, t)}{\partial t^2} \approx \frac{1}{(\Delta t)^2} \left(p_\mathbf{r}^{t + 1} - 2 p_\mathbf{r}^t + p_\mathbf{r}^{t - 1} \right) + O((\Delta t)^2)\tag{5}
∂t2∂2p(r,t)≈(Δt)21(prt+1−2prt+prt−1)+O((Δt)2)(5)
其中
p
r
t
p_\mathbf{r}^t
prt 表示
t
t
t 时刻的波场,
p
r
t
+
1
p_\mathbf{r}^{t + 1}
prt+1 表示
t
+
Δ
t
t + \Delta t
t+Δt 时间的.
O
O
O 表示同阶, 相应的数据被丢掉了.
根据链式法则, 可以计算损失
L
\mathcal{L}
L 对应对速度的梯度
∂
L
∂
v
(
r
)
=
∑
t
=
0
T
[
∂
L
∂
p
(
r
,
t
)
]
∂
p
(
r
,
t
)
∂
v
(
r
)
(7)
\frac{\partial \mathcal{L}}{\partial v(\mathbf{r})} = \sum_{t = 0}^T \left[\frac{\partial L}{\partial p(\mathbf{r}, t)}\right] \frac{\partial p(\mathbf{r}, t)}{\partial v(\mathbf{r})} \tag{7}
∂v(r)∂L=t=0∑T[∂p(r,t)∂L]∂v(r)∂p(r,t)(7)























 3750
3750











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








