非参检验之置换检验

原文链接：非参检验之置换检验https://mp.weixin.qq.com/s/3To6U_8ld79ctLtiCp5rjQ 

写在前面

置换检验（Permutation test）是属于非参检验的一种方法，特别适用于总体分布未知的小样本数据。在参数方法中，对于两种实验处理条件，我们一般假设两个总体为正态且方差齐性，然后使用双尾t检验来验证两者是否存在差异。通常零假设为两个总体的均值相等，接着计算t值，将其与理论分布相比较，如果t值落在95%置信区间之外，那么就可以拒绝零假设。

置换检验的思路有些不一样，我们先来看一个例子（来自参考文章1）。小明和小黑一起参加了一个数学补习班，培训前后分别测得的成绩如下表第一行所示，那么要如何判定补习班的成效呢（即成绩是否有了显著性提高）？

前后两次的测试让人直接想到了配对t检验，不过这种方法没法绕开它的前提假设（正态和等方差），而且这里的样本数有点少得可怜（2对），这时候本文的主角出场了。首先，建立置换检验的H0假设，即两次成绩不存在显著差异；接着，计算统计检验量，这里是两个样本的均值之差，即Ms=74-72.5=1.5；最后，在H0的前提下混合4个成绩，并进行排列组合，任取2个作为前测成绩，另2个作为后测成绩，结果如下所示（2~5行）。

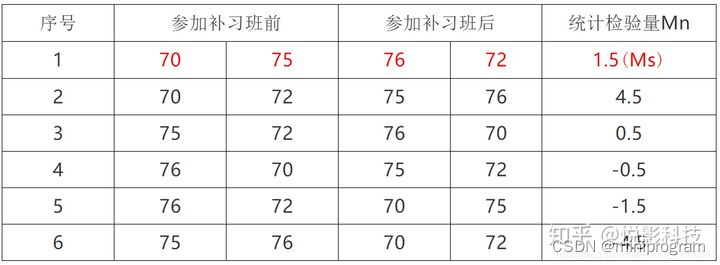
从表中我们看到除去第一行的原始数据，其它五行的统计检验量Mn大于1.5的有1个（第二行），那么估计的p值就等于1/5，矫正后（在抽样总体中加入一个远大于Ms的样本）的p值为(1+1)/(5+1)=1/3。很明显，p值大于0.05，因此结论是参加补习班未能显著提高成绩。置换检验就是如此操作，它不需要关于总体的任何假设，而且样本量可以非常小，因此使用起来显得很是得心应手。

配对t检验和置换检验之间的关系，让人想到皮尔逊（Pearson）相关和斯皮尔曼（Spearman）相关之间类似的关系。皮尔逊相关要求数据总体为正态、方差不能为零，且异常值对其影响很大，因此给实际分析带来了一定的局限性（假设不一定都成立，还得事后对其进行验证）。而斯皮尔曼相关是根据原始数据的排序等级进行计算求解的，如此事情就变得简单了，前面提到了几个限制统统都化解了，完美。

嗯，现在我们再来看另外一个例子来加深理解（正常点的，毕竟前面的例子仅仅是用来阐述概念的；来自参考文章2）。假设有个实验是为了验证某种生长素对拟南芥侧根数的增加是否有帮助。实验中的A组是加了生长素，其侧根数量为24 43 58 67 61 44 67 49 59 52 62 50（共12个）；B组则不加，其侧根数量为42 43 65 26 33 41 19 54 42 20 17 60 37 42 55 28（共16个）。

我们假设加入的生长素不会促进拟南芥的根系发育，那么A组和B组的数据可以认为是来自同一个总体。这次我们构建的检验统计量为两组侧根数目均值之差，原始数据中A组和B组均值之差为14。跟之前的简单示例相类似，混合后共有28个数据，然后每次随机取出12个作为A组，另外16个作为B组，并记录两组数据的均值之差。

如此反复操作总共进行999次，因为重复次数足够多了，我们能够得到如下的相对稳定的分布图，它代表了抽样的总体情况。

上图中除了展示999个数据分布的直方图，还画出了拟合曲线。直观上判断，原始数据两组均值之差14位于右尾，很有可能是在显著临界值附近，实际上大于14的数值有9个，计算p值(9+1)/(999+1)等于0.01，可以拒绝零假设，即实验表明加入生长素不会促进拟南芥的根系发育。

使用coin包

对于独立性问题coin包提供了全面的置换检验框架，它可以回答诸如不同组别之间的观测值是否独立（来自不同总体）、两个类别变量是否独立（不同水平之间存在差异）等问题，下图展示了与传统统计检验等价的、相对应的用于置换检验的coin函数（来自参考文章3）。

我们再次使用前面的拟南芥侧根数为分析对象，首先我们用传统的独立样本t检验方法来检验加入生长素是否会促进拟南芥根系的发育，这是一种需要前提假设和后续假设验证的方法，要求两样本对应的总体是正态，最好是方差也相等（R中默认假定方差不相等，并使用Welsh的修正自由度），代码和结果截图如下。

library(coin)
number <- c(24, 43, 58, 67, 61, 44, 67, 49, 59, 52, 62, 50, 42, 43, 65, 26, 33, 41, 19, 54, 42, 20, 17, 60, 37, 42, 55, 28)
# 将A重复12次、B重复16次
# coin包要求类别变量必须以因子形式编码
condition <- factor(c(rep("A",12),rep("B",16)))
mydata <- data.frame(condition, number)
# t.test(y~x, data)，y为数值型，x为二分变量
# 假定方差相等，并使用合并方差估计
t.test(number~condition, daya=mydata, var.equal=TRUE)

结果显示差异是显著的（见红框中的p值）。接下来我们使用相对应的coin中的置换检验函数，此时就可以完全抛开那些前提假设了，就此毫无顾忌地上代码、看结果。

# oneway_test(y ~ A)，A是分类因子，y是数值变量
# exact指出用精确的方式计算分布，即依据所有可能的排列组合，仅适用两样本情况
# 28选12，排列组合数高达三千多万，还好现在的计算资源比较廉价
oneway_test(number~condition, data=mydata, distribution="exact")

置换检验的p值与传统方法的p值差不太多，结果都很显著。以上从28个数据中取12个加16个的组合竟然已高达三千多万，实在有点让人吃惊，要是数据量再大些，所有排列组合的可能性将继续呈指数级增长，结果就不好控制而且也没必要。好在distribution参数还提供了其它的选项，如使用蒙特卡洛（MC）采样方法对抽样分布进行近似估计，设置参数为approximate(nresample=9999)即可，每次对混合的28个数据随机分成两组（一组12个、另一组16个），如此反复操作9999次，最后把实验数据放到这个近似分布中进行检验，结果图形如下。

这里没有设定随机数种子，例如set.seed(2089)，因此每次运行的结果会有些许的差异。另外，传统的单因素方差分析对应的coin函数也是同一个，一样的使用方法，只是结果不是显示Two-Sample而是K-Sample（用于高维采样），检验统计量由Z值变为卡方值。

使用lmPerm包

lmPerm包中提供的函数专门用来做回归分析和方差分析的置换检验，例如lmp()和aovp()函数分别对应传统的lm()和aov()函数。置换检验的函数名只是在原先名称之后加了个p，而且额外增加的参数主要是perm，选项值Exact跟coin包中的定义一模一样，根据所有可能的排列组合进行精确检验，不过默认当观测数大于10时自动会转成Prob选项；Prob选项随机不断抽样，直到满足特定的条件，如估计p值的估计标准误小于0.1*p，同时最大迭代次数也受maxIter参数限制；如果为空（“”）则生成F检验概率。

我们以一元线性回归模型（Yi=β0+β1Xi+εi）来举例说明置换操作是如何进行的。检验的对象是β1，零假设H0为β1=0。具体操作步骤如下（参考文章4）：

第一步，使用最小二乘法对参数β0和β1进行估计，得到的预测值和残差,然后构建β1的F型统计量T=(n-2)SSR/SSE，这里SSR指回归平方和、SSE指残差平方和；
第二步，对残差集合进行随机置换得到新的排序，并带入方程根据原有Xi得到新的Yi；
第三步，基于Xi和新的Yi重新拟合回归方程，得到新的β0和新的β1，并计算新的T值；
第四步，重复步骤2和3，直到满足迭代停止条件或达到限制次数，得到T值的集合；
第五步，计算近似p值，即T值集合中大于原始T值的数目除以总数。

现在我们来看一个具体例子。本公号的第一篇推文是回归诊断之正态性——画QQ图，在其中使用了R基础安装中的数据集women，包含15位年龄在30~39岁之间女性的身高和体重信息，现在我们使用lmp()函数来代替lm()函数进行拟合分析，结果如下图。

如果使用lm()函数来分析，其结果是类似的，只是这里的Iter列额外显示了迭代次数。

参考文章

1. 聊一聊置换检验Permutation test的原理
   https://zhuanlan.zhihu.com/p/328940140
2. Permutation Test 置换检验(转）
   https://blog.csdn.net/u011467621/article/details/47971917
3. [图书]R语言实战第十二章重抽样与自助法
4. 置换检验简介
   https://zhuanlan.zhihu.com/p/150954968
5. SSR、SSE、SST、R^2、调整R^2
   https://blog.csdn.net/qq_35182128/article/details/106346826