降维之探索性因子分析

最新推荐文章于 2025-01-08 01:00:00 发布

miniprogram

最新推荐文章于 2025-01-08 01:00:00 发布

阅读量737

点赞数 7

分类专栏： R语言画图文章标签： r语言

本文链接：https://blog.csdn.net/miniprogram/article/details/134529844

版权

R语言画图专栏收录该内容

9 篇文章

订阅专栏

（本文首发于公众号：R语言画图）

写在前面

有两种常用的变量降维方法，其一是主成分分析（PCA），我们在前面的文章中已学习，这次是其二方法——探索性因子分析（EFA）。PCA使用线性变换技术，将数据从原先的坐标系统变换到新的坐标系统中，并计算投射到各个坐标轴中数据的方差值，按大到小排序，第一坐标轴称为第一主成分，第二坐标轴称为第二主成分，以此类推。如此操作之后，因为主成分之间相互不相关，就解决了原始变量之间存在的信息重叠问题，用较少的新的变量最大化地对原始数据重新进行刻画，极大方便了后续的数据分析。

要是原始变量能够根据相互之间的相关程度分成几组，使得组间相关不大而组内变量间存在着一定的相关性，EFA方法就比较适用，它将相同本质的变量归入一个因子（可以解释多个变量间共有的方差，也被称为公共因子），以此达到降维的目的。PCA中的主成分是对原始变量进行加权组合（下图中间部分，来自参考文章1），表示观测变量的变异导致了主成分的变异，而EFA是一种识别无法直接观测变量（即潜在因子）的技术，潜在因子被视为引起观测变量变化的原因（下图右边部分），其中权重系数a表示因子对于复合而成的可观测变量的贡献值。

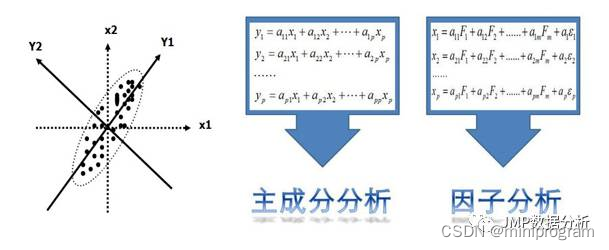
下图展示了PCA和EFA模型两者之间的区别（来自参考文章2）。左侧显示，主成分PC1和PC2是经由观测变量X1～X5的线性组合得到的，并且组合的权重系数使得主成分能够最大化所解释的方差。右侧因子F1和F2被当作是解释观测变量的原因，圆圈e1～e5代表观测变量方差的误差，它们是无法用因子来解释的，同样无法直接观测，但可以通过变量间的相互关系推导得到。

实例演示

这次用到R自带的Harman74.cor数据集，它的类型是列表（list），属于R中最复杂的一种数据类型了，其中可以包含各种类型的对象，如向量、矩阵、数据框和列表自身。Harman74.cor包含24个心理测验之间的相关系数矩阵，被试是145个七年级或八年级的学生。EFA的分析步骤与PCA很类似，首先需要判断提取几个因子，代码和图形如下。

# 小数点后数字的位数
options(digits=2)
# 查看数据
Harman74.cor$cov
library(psych)
# fa="both"指出同时做PCA和EFA
fa.parallel(Harman74.cor$cov,n.obs=145,fa="both",n.iter=100,main="并行分析碎石图")

上图除了显示碎石分析（蓝色）和平行分析（红色）外，还有y=1的水平线（黑色），PCA可以根据特征值大于1的准则选取成分，不过EFA的准则是特征值大于0。根据结果图，蓝线拐点以上或是红线之上的三角形有四个，因此我们选取的因子数是四个。

与PCA相比，提取公共因子的方法会更多一些，有最大似然法（ml）、主轴迭代法（pa）、最小残差法（minres）等，是在fa()函数中通过fm参数进行指定，代码和图形如下。

# 统计学家倾向于使用ml，当ml不会收敛时可使用pa
fa <- fa(Harman74.cor$cov,nfactors=4,rotate="none",fm="pa")
fa

图中显示四个因子能够解释24个心理测验48%的方差，只是载荷阵（黄框部分，变量与因子间的相关系数）的意义不太好解释，需要使用到因子旋转，代码和图形如下。

# varimax使用正交旋转，人为强制四个因子不相关
fa1 <- fa(Harman74.cor$cov,nfactors=4,rotate="varimax",fm="pa")
fa1

图中因子变得更好解释了。句子填空、单词含义、段落理解等在第一因子上载荷较大，视觉感知、立方体等在第三因子上载荷较大，加法、数点、编码等在第二因子上载荷较大，单词再认、数字再认、人物再认等在第四因子上载荷较大，剩下几项在四个因子上载荷比较平均，这些表明存在文字理解因子、空间视觉因子、数学计算因子和回忆再认因子。可以使用fa.diagram()函数来绘制因子旋转之后的结果，代码和图形如下。

# TRUE仅显示每项最大载荷（上图红框部分）与所对应的因子
fa.diagram(fa1,simple=TRUE)

除了正交旋转，还可以使用斜交转轴法（如promax）来旋转以上四个因子，此时允许因子之间存在相关，虽然变得复杂，但模型会更贴合实际数据，代码和图形如下。

# 需要安装GPArotation程序包
library(GPArotation)
fa2 <- fa(Harman74.cor$cov,nfactors=4,rotate="promax",fm="pa")
fa2

上图红框部分组成了因子模式矩阵，它们是标准化的回归系数，已经不是相关系数。我们照样可以得到文字理解因子、空间视觉因子、数学计算因子和回忆再认因子，虽然列的名称依然是PA1~PA4。黄框部分是因子关联矩阵，因子间的相关系数从047~0.59，相关性还是比较大的。同样我们可以使用fa.diagram()函数来绘制变量与因子间的相关系数图，这次还显示了因子之间的相关系数，代码和图形如下，这种图在有多个因子时非常实用。

# 这次我们使用FALSE选项，有些变量与多个因子都存中等程度的相关
fa.diagram(fa2,simple=FALSE)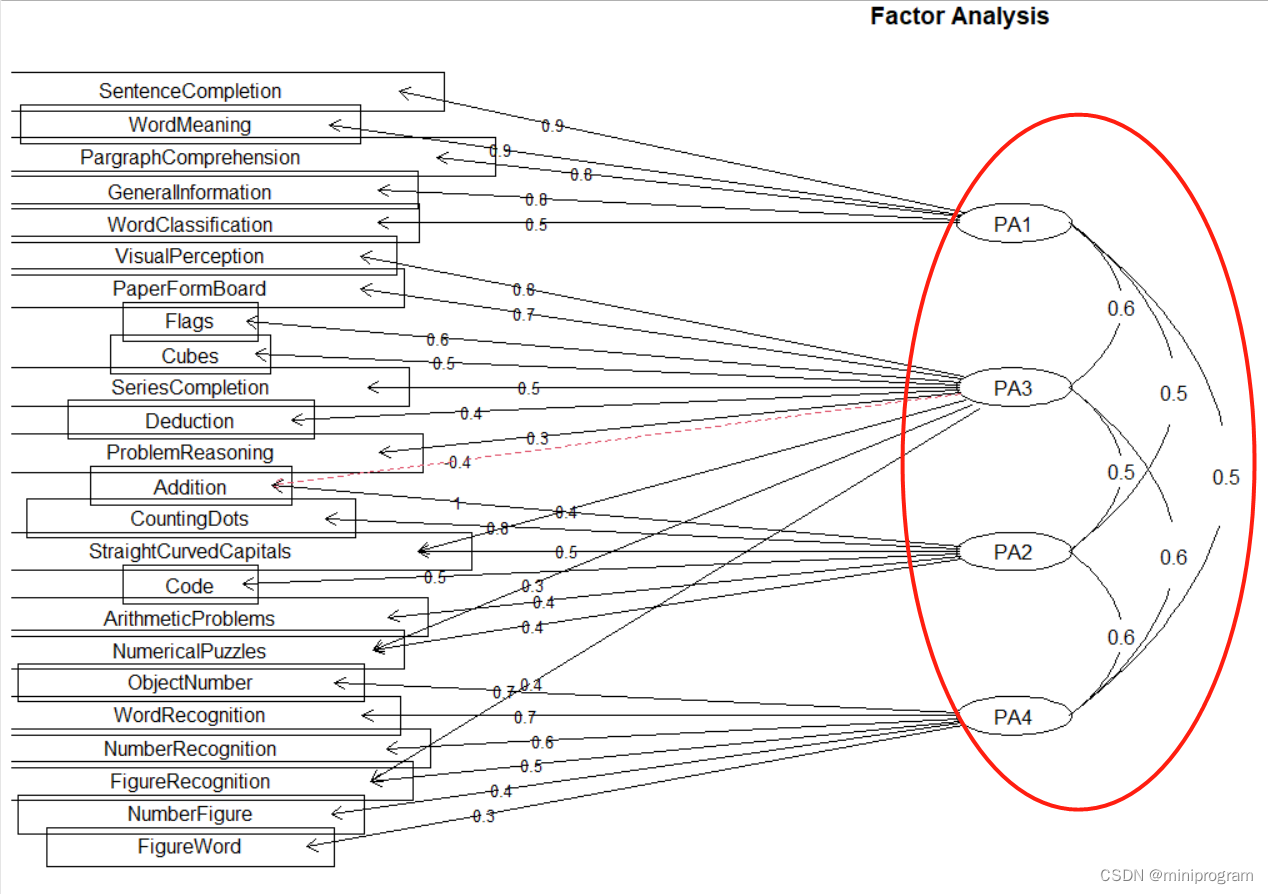

参考文章：

这样的数据分析员才有时间谈恋爱？
https://mp.weixin.qq.com/s?__biz=MjM5MDA3NjYyOQ==&mid=2650056454&idx=1&sn=162a3941a1e7e2f57f6da6c834c6aa70&chksm=be4a5cbc893dd5aa9a03f4595c7a490aa2408182650d8af0893ea31e932837ae2746138549e5&scene=21
[图书]R语言实战第十四章主成分和因子分析
R自带数据集介绍
https://www.cnblogs.com/adam012019/p/14918647.html