K近邻算法
KNN是通过测量不同特征值之间的距离进行分类。它的的思路是:如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。K通常是不大于20的整数。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。下图红色,蓝色,代表不同类别的样本,绿色代表待分样本。
上图的表述并不准确,应该是选取距离绿色点最近的k个样本,而没有画出来的这个圈的范围,(固定大小的圈,圈中各种类型的点来计数,待分样本依据圈中某类样本数多分类,这种想法是错误的)。应该是选取固定数量的样本,因为样本的分布范围不均匀,所以圈是不固定大小的。
KNN算法
优点:
对异常值不敏感,无数据输入假定,精度高
缺点:
计算复杂度很高
k值的选择对结果影响大
数据不平衡情况下,表现很差
KNN适用于数值型的标称数据
k近邻的距离度量
1)曼哈顿距离(街区距离)
2)欧式距离
3)余弦距离
K值的选择
1)选择较小的K值
学习的近似误差会减小,学习的估计误差会变大
噪声敏感
k值小 意味着整体模型复杂,容易过拟合。
k近邻算法的算法:KD树
kd树是一种对 K维空间的实例点进行存储以便对其进行快速检索的树形数据结构
kd树是二叉树
不断用垂直于坐标平面的超平面将K维空间切分,形成K 维超矩形区域
kd树的构造算法:
1)构造根节点
计算输入的所有样本每个维度(样本的列方向)的方差(a1,a2,a3,a4,a5,....,an),选择方差最大的维作为第一个切分的维度,方差大,说明数据在这个维度分的比较开。按这个维度的维度值对样本从大到小排序,选择中位数的样本,切开空间,样本被分为2部分。
2)再在前面划分的子空间进行再次划分。
3)结束条件:直到此空间中只包含一个数据点。
kd树的构造实例:
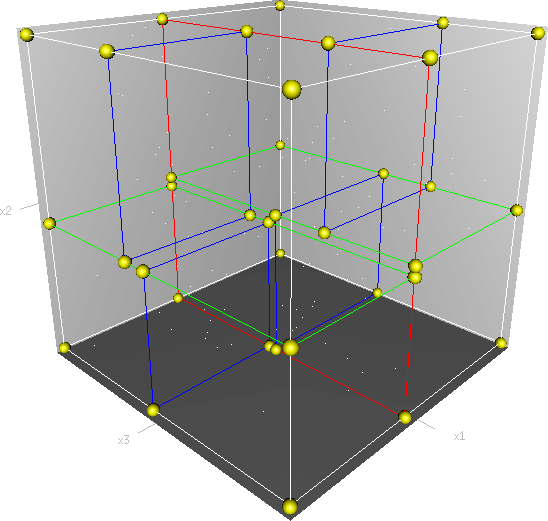
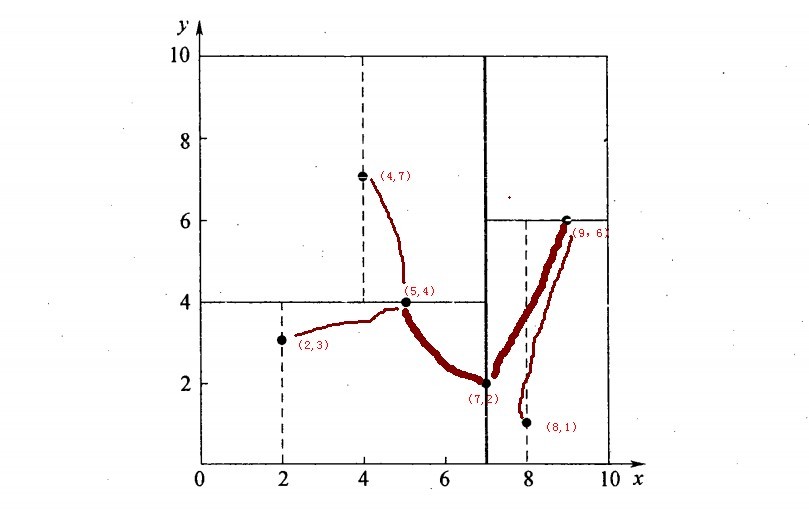
假设有6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间内,如下图所示。为了能有效的找到最近邻,k-d树采用分而治之的思想,即将整个空间划分为几个小部分,首先,粗黑线将空间一分为二,然后在两个子空间中,细黑直线又将整个空间划分为四部分,最后虚黑直线将这四部分进一步划分。
6个二维数据点{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}构建kd树的具体步骤为:
- 确定:split域=x。具体是:6个数据点在x,y维度上的数据方差分别为39,28.63,所以在x轴上方差更大,故split域值为x;
- 确定:Node-data = (7,2)。具体是:根据x维上的值将数据排序,6个数据的中值(所谓中值,即中间大小的值)为7,所以Node-data域位数据点(7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于:split=x轴的直线x=7;
- 确定:左子空间和右子空间。具体是:分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点={(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点={(9,6),(8,1)};
kd树的插入
kd树的插入与二叉树的插入类似。
kd树的最近邻搜索
通过二叉搜索,顺着搜索路径很快找到最邻近的叶子节点,但是这个叶子节点和并不一定是最近邻的点,需要进行回溯操作,也就是沿着搜索路径方向查询是否有更加的数据点。
举例:查询点(2.1,3.1)
星号表示要查询的点(2.1,3.1)。通过二叉搜索,顺着搜索路径很快就能找到最邻近的近似点,也就是叶子节点(2,3)。而找到的叶子节点并不一定就是最邻近的,最邻近肯定距离查询点更近,应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻,还需要进行相关的‘回溯'操作。也就是说,算法首先沿搜索路径反向查找是否有距离查询点更近的数据点。
以查询(2.1,3.1)为例:
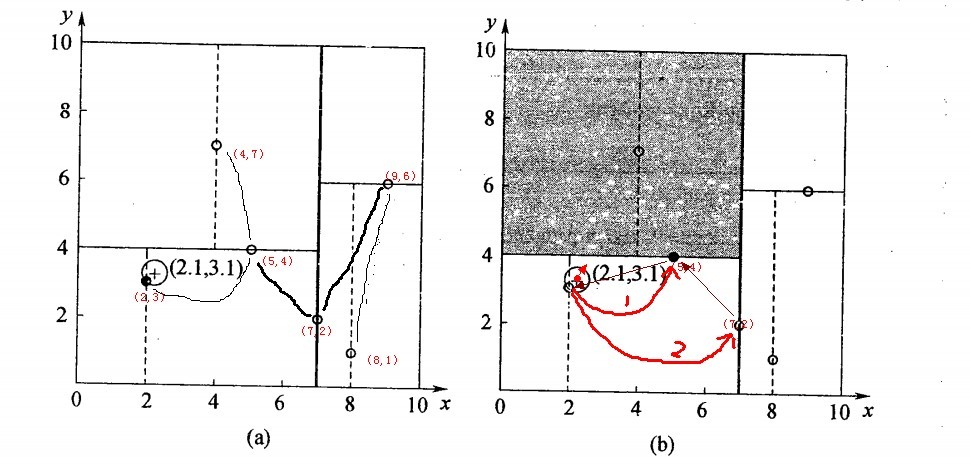
- 二叉树搜索:先从(7,2)点开始进行二叉查找,然后到达(5,4),最后到达(2,3),此时搜索路径中的节点为<(7,2),(5,4),(2,3)>,首先以(2,3)作为当前最近邻点,计算其到查询点(2.1,3.1)的距离为0.1414,
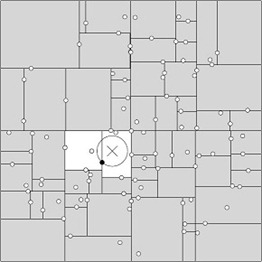
- 回溯查找:在得到(2,3)为查询点的最近点之后,回溯到其父节点(5,4),并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以(2.1,3.1)为圆心,以0.1414为半径画圆,如下图所示。发现该圆并不和超平面y = 4交割,因此不用进入(5,4)节点右子空间中(图中灰色区域)去搜索;
- 最后,再回溯到(7,2),以(2.1,3.1)为圆心,以0.1414为半径的圆更不会与x = 7超平面交割,因此不用进入(7,2)右子空间进行查找。至此,搜索路径中的节点已经全部回溯完,结束整个搜索,返回最近邻点(2,3),最近距离为0.1414。
2.5.2、举例:查询点(2,4.5)
一个复杂点了例子如查找点为(2,4.5),具体步骤依次如下:
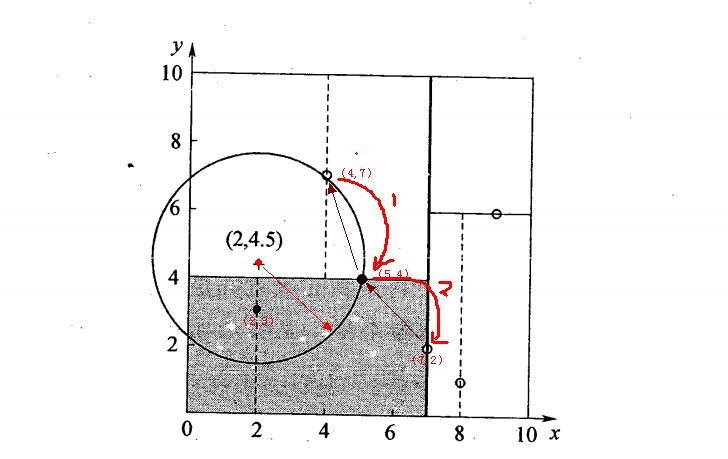
- 同样先进行二叉查找,先从(7,2)查找到(5,4)节点,在进行查找时是由y = 4为分割超平面的,由于查找点为y值为4.5,因此进入右子空间查找到(4,7),形成搜索路径<(7,2),(5,4),(4,7)>,但(4,7)与目标查找点的距离为3.202,而(5,4)与查找点之间的距离为3.041,所以(5,4)为查询点的最近点;
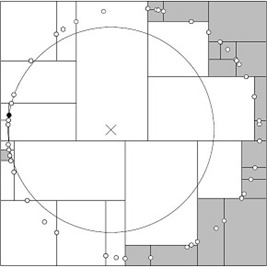
- 以(2,4.5)为圆心,以3.041为半径作圆,如下图所示。可见该圆和y = 4超平面交割,所以需要进入(5,4)左子空间进行查找,也就是将(2,3)节点加入搜索路径中得<(7,2),(2,3)>;于是接着搜索至(2,3)叶子节点,(2,3)距离(2,4.5)比(5,4)要近,所以最近邻点更新为(2,3),最近距离更新为1.5;
- 回溯查找至(5,4),直到最后回溯到根结点(7,2)的时候,以(2,4.5)为圆心1.5为半径作圆,并不和x = 7分割超平面交割,如下图所示。至此,搜索路径回溯完,返回最近邻点(2,3),最近距离1.5。
上述两次实例表明,当查询点的邻域与分割超平面两侧空间交割时,需要查找另一侧子空间,导致检索过程复杂,效率下降。
研究表明N个节点的K维k-d树搜索过程时间复杂度为:tworst=O(kN1-1/k)。
http://blog.csdn.net/app_12062011/article/details/51986805 此网址有更加详细的介绍。






















 792
792

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








