机器学习-支持向量机（SVM）

1.支持向量机（SVM）简介

        支持向量机（Support Vector Machine，简称SVM）是一种按监督学习方式对数据进行二元分类的广义线性分类器。它的决策边界是对学习样本求解的最大边距超平面。

        SVM是一种常见的分类算法，它被广泛应用于模式识别、文本分类、图像分类等许多领域。SVM的主要思想是将样本点映射到高维空间中，使得样本点在高维空间中形成一种线性可分或近似线性可分的状态，从而将原始的样本点分类问题转化为高维空间中的线性分类问题。

2.超平面最大间隔

        超平面最大间隔指这个超平面到两类样本中最远的一个样本的距离。寻找一个超平面，使得这个超平面到所有支持向量的距离最大化。

        划分超平面的公式

        

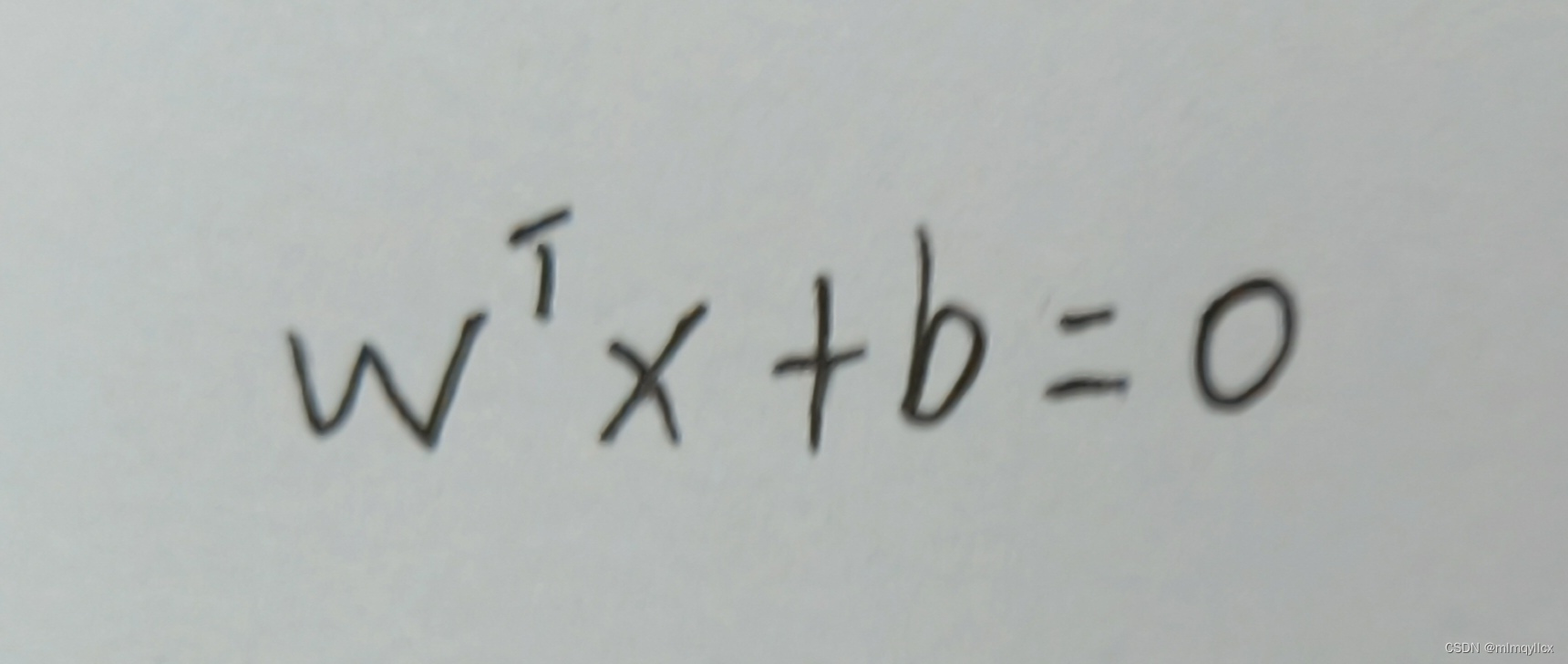
        输入数据：x=（x1,x2,x3...xn）,n为数据的维度

        法向量：w=（w1,w2,w3...wn）,法向量决定超平面的方向

        位移项：b，超平面到原点的距离

        找到一个超平面wx+b=0，使得在超平面上方的点x代入函数y=wT x+b，y全部大于0，在超平面下方的点x代入函数y=wTx+b，y全部小于0。

        支持向量到超平面的距离

        

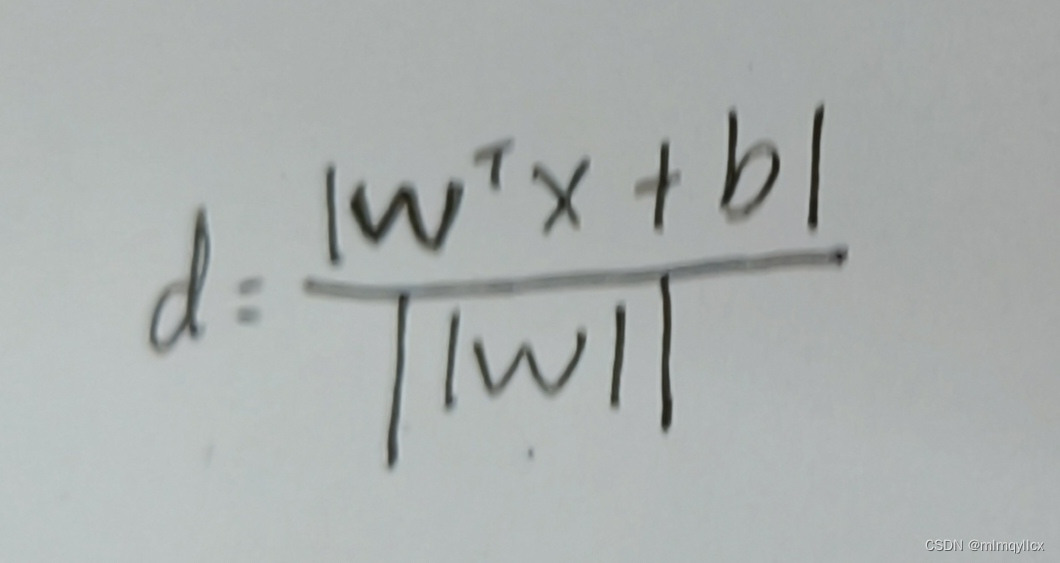
        两类样本边界的距离

        

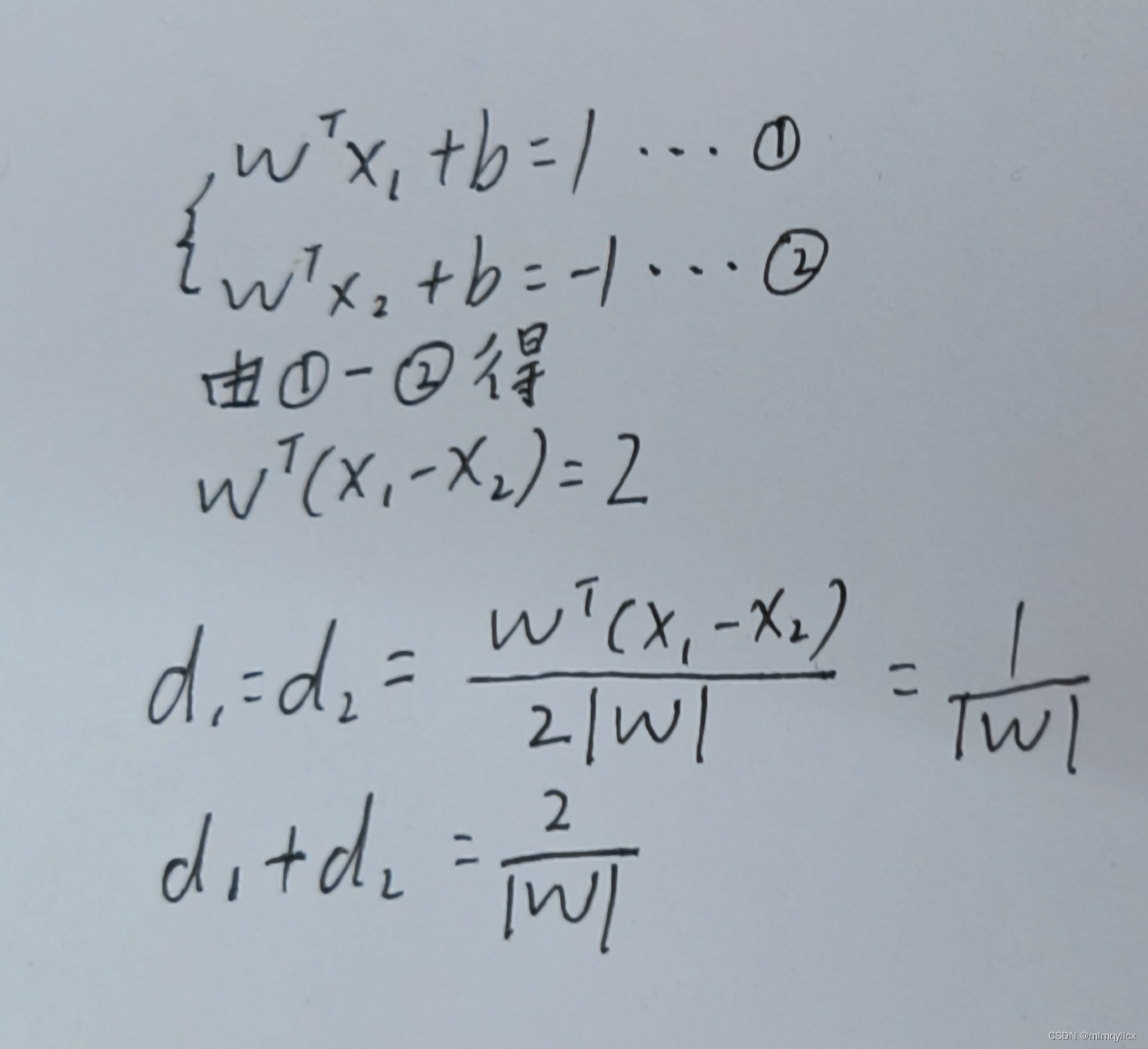
        硬间隔与软间隔

        硬间隔：严格地让所有实例都不在最⼤间隔之间， 并且位于正确的⼀边

        软间隔：使⽤更灵活的模型，让⽬标尽可能在保持最⼤间隔宽阔和限制间隔违例之间找到良好的平衡

        核函数

        当处理线性不可分情况时，线性分类器无法解决这种情况，使用核函数

        成为核函数的条件：对称矩阵，半正定矩阵

3.具体实现

        确定平面（软间隔与正则化）

        正则化（Regularization）是机器学习中的一种重要技术，主要用于防止模型过拟合。

        正则化的基本思想是在模型的损失函数中加入一个额外的项，这个项与模型的复杂度有关。简单来说，正则化项会惩罚那些可能导致模型复杂度增加的参数。

        在SVM中，正则化通常用于控制模型的复杂度。正则化项通常与模型的权重向量w有关，通过调整正则化参数，可以平衡模型的复杂度和拟合能力。

        相关代码：

def __init__(self, learning_rate=0.002, lambda_param=8, n_iters=10000):  
    
    self.lr = learning_rate  # 学习率  
    self.lambda_param = lambda_param  # 正则化参数  
    self.n_iters = n_iters  # 训练次数  
    self.w = None  # 权重     
    self.b = None    
  
def fit(self, X, y):  
    y_ = np.where(y <= 0, -1, 1)  # 将标签转换为+1或-1  
    n_samples, n_features = X.shape  # 获取特征矩阵的形状  
      
    self.w = np.zeros(n_features)  # 初始化权重为零向量  
    self.b = 0  # 初始化偏置为零  
          
    for _ in range(self.n_iters):  # 迭代次数等于训练次数  
        for idx, x_i in enumerate(X):  # 遍历每个样本  
            condition = y_[idx] * (np.dot(x_i, self.w) - self.b) >= 1  # 计算条件判断  
            if condition:  # 如果满足条件，则更新权重和偏置  
                self.w -= self.lr * (2 * self.lambda_param * self.w)  
            else:  # 如果不满足条件，则更新权重和偏置，并加上正则化项  
                self.w -= self.lr * (2 * self.lambda_param * self.w - np.dot(x_i, y_[idx]))  
                self.b -= self.lr * y_[idx]  # 添加正则化项到偏置中

        绘制SVM决策边界

def plot_decision_boundary(X, y, svm):  
    # 创建网格覆盖决策区域  
    x1 = np.linspace(np.min(X[:, 0]) - 1, np.max(X[:, 0]) + 1, 100)  
    x2 = np.linspace(np.min(X[:, 1]) - 1, np.max(X[:, 1]) + 1, 100)  
    xx1, xx2 = np.meshgrid(x1, x2)  
    grid = np.c_[xx1.ravel(), xx2.ravel()]  
      
    # 使用SVM模型预测每个网格点的类别  
    pred = svm.predict(grid)  
    pred = pred.reshape(xx1.shape)  
      
    # 绘制决策边界和训练数据点  
    plt.contour(xx1, xx2, pred, levels=[-1, 1], colors='k')  
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap='bgr')  
    plt.xlabel('Feature 1')  
    plt.ylabel('Feature 2')  
    plt.show()

4.总结

        SVM在只有少数样本的情况下也可以取得较好的分类效果，这使得它在一些数据量较小的领域中具有很好的应用价值。

        SVM在进行分类时，不需要过多的特征工程，能够自动地根据样本点在高维空间中的分布情况来进行分类，因此对于特征的权重和数量并不敏感。

        SVM在进行分类时，会尽量寻找一个最优的超平面来将样本点分开，因此对于噪声数据和异常值的干扰具有较强的鲁棒性。

        SVM不仅可以用于二分类问题，也可以扩展到多分类问题中，这使得它在许多领域中都具有广泛的应用。