摄影测量中的计算机视觉之基础知识.

计算机视觉说白了也就是在和图像打交道, 而图像就是一个投影空间.
现实世界中的物体在照片中会改变大小形状.
但是有一些东西是不变的, 就比如点还是点, 直线还是直线,圆还是圆(可能是椭圆)
对一幅图旋转和平移不会改变它的长度和体积,距离角的比值,几何中心,平行关系以及和
均匀缩放
不均匀缩放,剪切

重合几何(incidence)
主要就是包含点的共线和线的相交. 也就是说,经过投影后, 如果原来点${\mathbf{X}}_1$,${\mathbf{X}}_2$,${\mathbf{X}}_3$在同一条直线$\mathbf{l}$上,那么它们变换后还是在同一条直线上.
如果原来线${\mathbf{l}}_1$,${\mathbf{l}}_2$,${\mathbf{l}}_3$相交于同一点$\mathbf{X}$,那么它们变换后还是相交于用一个点.

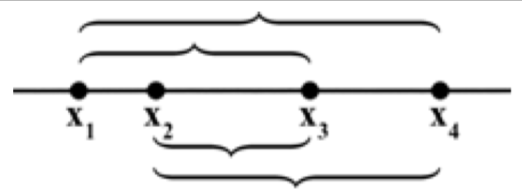
交比(Cross Ratio)
主要就是说,共线的四个点,经过投影变换后,点${\mathbf{X}}_1$和点${\mathbf{X}}_3$之间的距离乘上点${\mathbf{X}}_2$和点${\mathbf{X}}_4$之间的距离, 再除以(点${\mathbf{X}}_1$和点${\mathbf{X}}_4$之间的距离乘以点${\mathbf{X}}_2$)和点${\mathbf{X}}_3$),这个比值是不变的.
$$CR\left({\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,{\mathbf{x}}_4\right)=\frac{d\left({\mathbf{x}}_1,{\mathbf{x}}_3\right)\cdot d\left({\mathbf{x}}_2,{\mathbf{x}}_4\right)}{d\left({\mathbf{x}}_1,{\mathbf{x}}_4\right)\cdot d\left({\mathbf{x}}_2,{\mathbf{x}}_3\right)}$$

什么是齐次坐标系呢?
其实就是点和线在投影空间中的表示.
投影空间的特点就是一个向量,和这个向量的倍数代表的是同一个实体.
一个图像点$(x,y{)}^{\mathrm{T}}$在投影空间${\mathbb{P}}^2$可以用一个3-vector表示:
$$\mathbf{x}=\lambda \cdot (x,y,1{)}^{\mathrm{T}}=(u,v,w{)}^{\mathrm{T}}$$
$$\Vert \mathbf{x}\Vert =\sqrt{u^2+v^2+w^2}\ne 0$$
这个w被叫做齐次分部.
x,y是欧几里得分部.
$$x=\frac{u}{w}\text{ and }y=\frac{v}{w}\text{ for }w\ne 0$$
点的表达: Euclidean normalized
$$\mathbf{x}=\frac{1}{w}\left(\begin{array}{c}u\\ v\\ w\end{array}\right)=\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$
线的表达:HESSIAN normal form (except for the sign of d )
$$\mathbf{l}=\frac{1}{\sqrt{\frac{1}{a^2+b^2}}}\left(\begin{array}{l}a\\ b\\ c\end{array}\right)=\left(\begin{array}{c}\cos \varphi \\ \sin \varphi \\ d\end{array}\right)$$
这里好像也没说线的其次分部必须为0,不过在其它资料上看到的都是其次分部为0.

一些性质:点和线的二元性
重合关系:
$${\mathbf{x}}^{\top }\mathbf{l}={\mathbf{l}}^{\top }\mathbf{x}=au+bv+cw=0$$
线的相交:
$$\begin{array}{rl}& \mathbf{x}={\mathbf{l}}_1\times {\mathbf{l}}_2\\ & \det \left[\begin{array}{lll}{\mathbf{l}}_1& {\mathbf{l}}_2& {\mathbf{l}}_3\end{array}\right]=0\end{array}$$

点的共线:
$$\begin{array}{rl}& \mathbf{l}={\mathbf{x}}_1\times {\mathbf{x}}_2\\ & \det \left[\begin{array}{lll}{\mathbf{x}}_1& {\mathbf{x}}_2& {\mathbf{x}}_3\end{array}\right]=0\end{array}$$

另外一个特别重要的就是理想点(无限远点)和理想线(无限远线).
理想点:
$${\mathbf{x}}_{\infty }=(u,v,0{)}^{\top }$$
理想线:
$${\mathbf{I}}_{\infty }=(0,0,c{)}^{\top }$$
两条平行线相交于无限远点:
$${\mathbf{l}}_1\times {\mathbf{l}}_2=(b,-a,0{)}^{\top }$$

投影空间:
$${\mathbf{P}}^2={\mathbf{R}}^2\cup {\mathbf{x}}_{\infty }\cup {\mathbf{l}}_{\infty }$$

还有一个比较重要的:
如果H是从一个投影空间到令一个空间的转化.那么
对于点的转化是:
$${\mathbf{x}}^{\prime }=\mathbf{H}\mathbf{x}$$

对于线的转化是:
$${\mathbf{l}}^{\prime }={\left({\mathbf{H}}^{-1}\right)}^{\top }\mathbf{l}={\mathbf{H}}^{-\mathbf{T}}\mathbf{l}$$

参考:
https://en.wikipedia.org/wiki/Cross-ratio
https://en.wikipedia.org/wiki/Incidence_(geometry)