如何通过实验数据确定Weibull分布的形状参数和尺度参数？

通过实验数据确定Weibull分布的形状参数（k）和尺度参数（λ）的方法有多种，以下是基于我搜索到的资料总结的详细步骤和方法：

1. 最大似然估计法（MLE）

最大似然估计法是常用的参数估计方法之一，适用于Weibull分布。其基本思想是通过最大化似然函数来估计参数。具体步骤如下：

• 定义似然函数：假设有一组样本数据 1,2,…,x1​,x2​,…,xn​，Weibull分布的概率密度函数为：

  

  对于样本数据，似然函数为：

  

• 对数似然函数：取对数简化计算：

  

• 求解参数：通过求解对数似然函数关于 k 和 λ 的偏导数并令其等于零，得到参数的估计值。

验证抽检方案示例

2. 矩估计法（Method of Moments, MoM）

矩估计法通过匹配样本矩与理论矩来估计参数。具体步骤如下：

• 计算样本矩：计算样本的均值 ˉxˉ 和方差2s2。

• 理论矩：Weibull分布的理论均值和方差分别为：

  

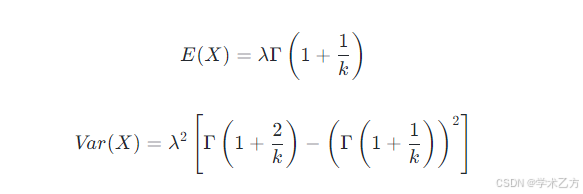
• 解方程组：通过匹配样本均值和方差与理论均值和方差，建立方程组求解 k 和 λ。

SOLVED: The Weibull distribution has a distribution function: F(c) = 1 ...

3. 分位数法（Quantile Method）

分位数法通过匹配样本分位数与理论分位数来估计参数。具体步骤如下：

• 计算样本分位数：选择合适的分位数（如中位数、四分位数等）。

• 理论分位数：Weibull分布的理论分位数可以通过累积分布函数（CDF）计算：

  

• 解方程：通过匹配样本分位数与理论分位数，建立方程求解 k 和 λ。

Distribución de Weibull

4. 贝叶斯方法

贝叶斯方法结合先验信息和实验数据来估计参数。具体步骤如下：

• 选择先验分布：选择合适的先验分布（如伽马分布）。
• 后验分布：通过贝叶斯公式计算后验分布。
• 参数估计：从后验分布中提取形状参数和尺度参数的估计值。

weibull分布的几种形式_weibull累积分布函数-CSDN博客

5. 图形方法

图形方法通过绘制Weibull分布的拟合曲线来直观判断参数。具体步骤如下：

• 绘制概率图：使用Weibull概率图（如概率纸）将数据点拟合到Weibull分布曲线中。
• 估计参数：通过观察曲线的形状和位置，手动调整参数以匹配数据点。

Python SciPy stats.ppcc_plot用法及代码示例 - 纯净天空

6. 其他方法

• L-moment方法：通过L-moment（L-矩）来估计参数，适用于处理非正态分布的数据。
• 蒙特卡洛模拟：通过模拟生成大量样本数据，分析其统计特性来估计参数。

  

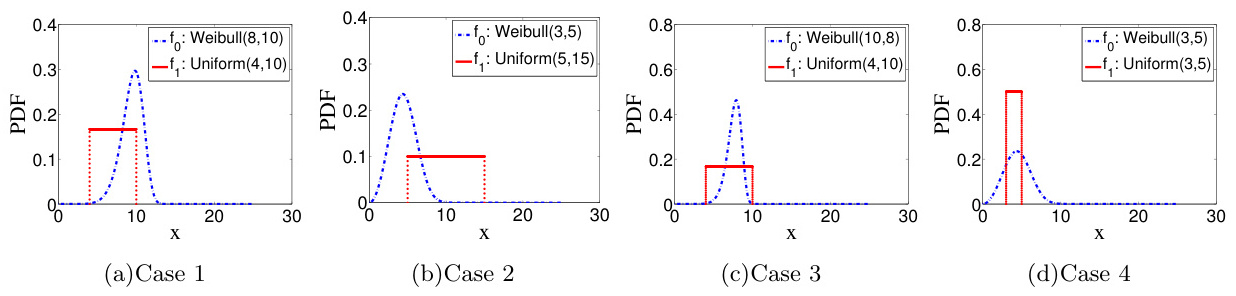
注意事项

1. 数据质量：确保实验数据的质量和完整性，避免异常值对参数估计的影响。
2. 方法选择：根据数据的特点和需求选择合适的估计方法。例如，MLE适用于大规模数据，而矩估计法适用于小样本数据。
3. 验证结果：通过残差分析或拟合优度检验（如Kolmogorov-Smirnov检验、Cramer-von Mises检验等）验证参数估计的准确性。

   

    

   

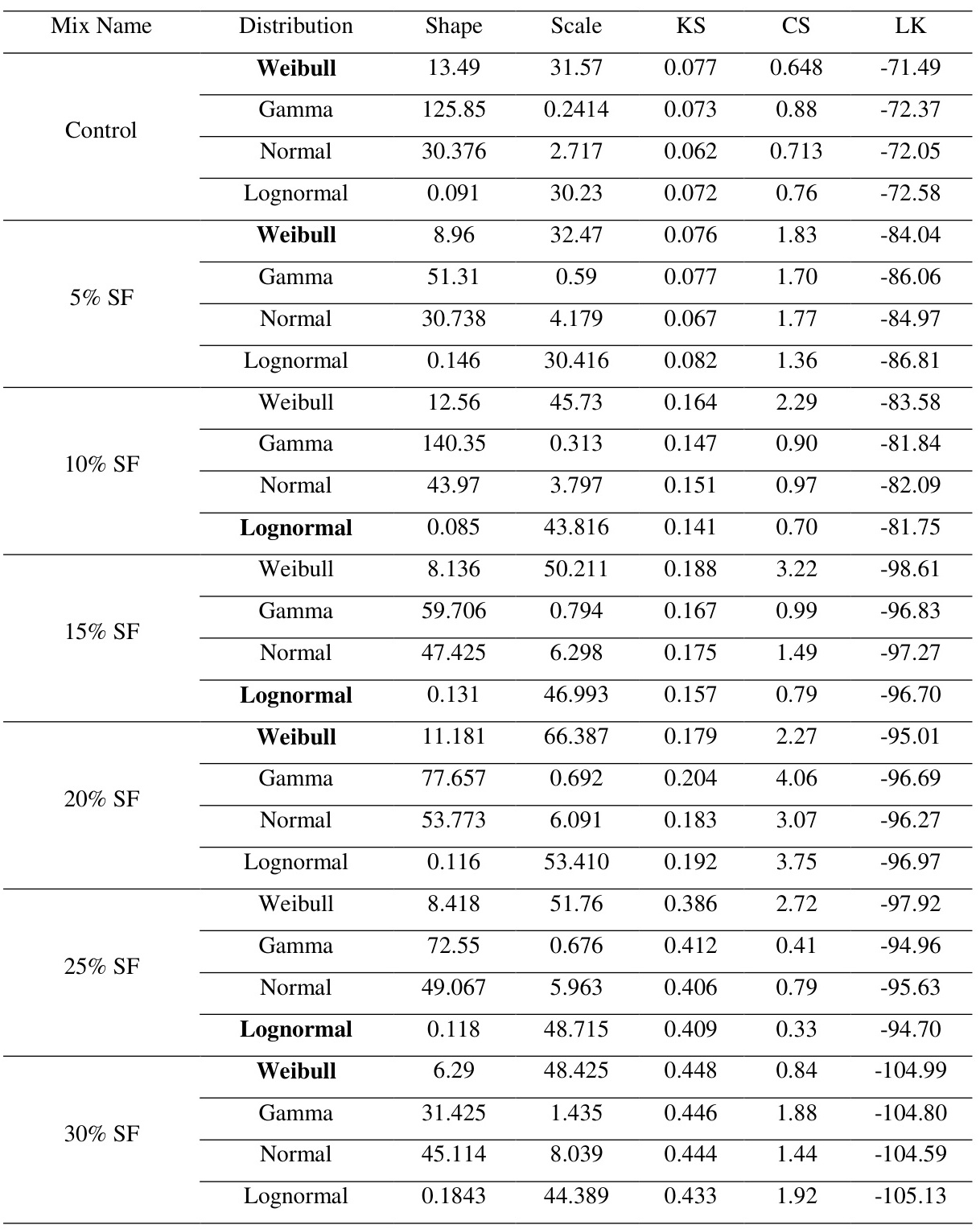
通过上述方法，可以有效地从实验数据中确定Weibull分布的形状参数和尺度参数，从而为后续的分析和建模提供可靠的基础。

关注博主，有些文章只有粉丝可见！