欧拉角及其旋转矩阵，旋转顺序与内旋/外旋及其代码

目录

欧拉角介绍

旋转矩阵公式推导

旋转顺序

内旋/外旋

---

欧拉角介绍

欧拉角：

横滚：roll（绕X轴旋转）；

俯仰：pitch（绕Y轴旋转）；

偏航（也称航向角）：yaw或者heading（绕Z轴旋转）。

注意：一般xyz坐标轴为前左上（KITTI数据集），或者右前上（华测惯导），或者前右下（常见于国外教材）等等，可以随意定义，（这是惯性坐标系，i系）。而当右前上时，xyz对应的旋转分别是pitch,roll, yaw，且pitch头向上为正，和前左上时正方向相反。前右下的yaw和前左上正方向相反。

 （总结：注意坐标轴方向的定义及正方向问题）

注意2：yaw是全局角度，一般以正北为0，逆时针为正（国产惯导）；也可以定义为正东为0，逆时针为正（KITTI数据集）；也可以是其他任意定义。

（总结：注意yaw的方向和旋转正方向）

注意3：roll和pitch一般范围为±90°，yaw的角度范围为0~360°或-180~180°，需要根据实际需要进行变换。

（总结：注意yaw的范围）

可视化说明参照：pitch、yaw、roll三个角的区别-CSDN博客

旋转矩阵公式推导

旋转符合右手定则。假设旋转轴顺序为zyx，分别对应yaw（γ）、pitch（β）、roll（α），则旋转矩阵表示为：

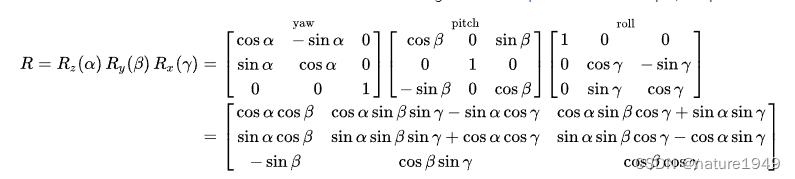
 旋转矩阵的推导资料很多了，此处不加赘述。

本文章主要针对旋转顺序和内旋/外旋做明确的解释。

旋转顺序

旋转顺序可以是任意设置的。但常见的默认顺序是zyx，对应yaw，pitch，roll。尤其是在做INS/GPS全局局部数据互相转化时。

注意：旋转顺序不同结果也不同，不能随意改变。比如zyx对应yaw,pitch,roll，与xyz对应roll,pitch,yaw的旋转矩阵都是不同的，对应的点或向量的变换结果也不同。随意改变旋转顺序结果就是错的。

默认按照zyx对应yaw，pitch，roll进行旋转！！！

内旋/外旋

内旋：每个基本旋转都是在先前操作旋转的坐标系上执行的。

也就是说，比如绕z旋转之后再绕y轴旋转，这个y轴就是旋转之后的新y轴。

外旋：每次旋转都是围绕世界坐标系的轴进行的，世界坐标系不移动。

也就是说，比如绕z旋转之后再绕y轴旋转，这个y轴还是变换之前的那个y轴。

import numpy as np
from scipy.spatial.transform import Rotation as Rot

point = np.array([1,0,0])
rpy = np.array([0, np.pi/4, np.pi/2])

#####################        内旋
# 内旋@need_trans_point = 对n坐标系中的点进行活动坐标旋转后（将n系中的点转到b系中后）（也就是b坐标系中的点）在n坐标系下的位置，用ZYX，ypr，此中need_trans_point表示在n系下的初始位置。和下面一个意思。
# 内旋@need_trans_point =   b坐标系中的点在n坐标系下的位置，用ZYX，ypr，此中need_trans_point表示在b系下的初始位置
# 内旋.T@need_trans_point = n坐标系中的点在b坐标系下的位置，用ZYX，ypr，此中need_trans_point表示在n系下的初始位置
nx=Rot.from_euler('ZYX', rpy[::-1], degrees=False).as_matrix()   ##  注意：zyx需要对应yaw，pitch，roll。
nx1=Rot.from_euler('xyz', rpy, degrees=False).as_matrix()        ##  每种特定顺序的外旋等价于其相反顺序的内旋。结果和上面等价

#####################        外旋
# 外旋@need_trans_point = 对原坐标系中的点进行固定坐标旋转后在原坐标系下的位置，用zyx，ypr，此中need_trans_point表示在n系下的初始位置
# 外旋.T@need_trans_point = 原坐标系中的点在经固定坐标旋转后的新坐标系下的位置，用zyx，ypr
wx=Rot.from_euler('zyx', rpy[::-1], degrees=False).as_matrix()
wx1=Rot.from_euler('XYZ', rpy, degrees=False).as_matrix()

print(wx@point, wx1@point, nx@point, nx1@point, )
print(wx.T@point, wx1.T@point, nx.T@point, nx1.T@point,)

内旋与外旋详细区别参考代码及其注释。

解释：以上代码以scipy，rotation为工具。其中，'ZYX'大写为内旋，'zyx'小写时为外旋（具体参照下面官方说明）。

可查看scipy文档有关rotation说明：

https://www.osgeo.cn/scipy/reference/generated/scipy.spatial.transform.Rotation.from_euler.htmlhttps://www.osgeo.cn/scipy/reference/generated/scipy.spatial.transform.Rotation.from_euler.html

可借助在线工具计算内旋的旋转矩阵（旋转顺序yaw,pitch,roll，对应zyx）：Rotation Tool

欢迎交流！