MaxViT（ECCV 2022, Google）论文与代码解析

最新推荐文章于 2025-03-28 16:33:04 发布

00000cj

最新推荐文章于 2025-03-28 16:33:04 发布

阅读量2.1k

点赞数 19

分类专栏： Transformer 文章标签：深度学习计算机视觉 Transformer 人工智能 Google

本文链接：https://blog.csdn.net/ooooocj/article/details/140170768

版权

Transformer 专栏收录该内容

43 篇文章

订阅专栏

paper：MaxViT: Multi-Axis Vision Transformer

official implementation：https://github.com/google-research/maxvit

third-party implementation：https://github.com/huggingface/pytorch-image-models/blob/main/timm/models/maxxvit.py

出发点

现有的视觉模型中的自注意力机制在处理大尺寸图像时存在可扩展性问题。具体来说，自注意力的计算复杂度随着输入图像的尺寸呈平方增长，导致在高分辨率图像或大批量数据时计算资源和时间成本过高。

创新点

MaxViT 提出了一种新的视觉模型架构，结合了局部和全局的注意力机制，以解决传统自注意力模型在计算复杂度和效率上的不足。通过这种方式，MaxViT 能在处理大尺寸图像时保持高效，同时提升模型性能。具体包括

混合注意力机制： MaxViT 将局部注意力和全局注意力结合，使得模型既能捕捉局部细节，又能理解全局上下文。
分层架构： 采用分层结构，在每一层中分别进行局部和全局处理，从而在不同尺度上提取特征。
高效计算： 通过创新的架构设计，大幅降低了自注意力机制的计算复杂度，使其在高分辨率图像上的应用更加实用。

方法介绍

与卷积相比，全局交互式self-attention的关键优势之一。但直接沿着整个空间维度计算self-attentioin是不可行的，因为计算需要二次方复杂度。为了解决这个问题，本文提出了一种multi-axis多轴方法，将full-size的注意力分解成两种稀疏形式 —— 局部和全局。

如图3所示，左侧是本文提出的Block Attention，即将特征图划分为多个局部窗口，然后在每个窗口内计算self-attention，实现局部信息的交互。其实这里和swin transformer的window-based self-attention是一样的（具体介绍Swin Transformer（ICCV 2021）论文与代码解析-CSDN博客）。

图3右侧是本文提出的稀疏全局attention - Grid Attention，左侧的Block Attention是在相同颜色的窗口内计算attention，grid attention也是在相同颜色的像素点间计算attention只不过相同颜色的像素点均匀稀疏分布整个feature map上，从而实现全局信息交互。这里有点类似于膨胀卷积。

图3是一个完整的MaxViT block，其中除了sequntial连接的block attention和grid attetion，前面还加上了MBConv block且其中使用了SE block，由于MBConv block中的深度卷积可以看做是一种条件位置编码（具体介绍见CPVT（ICLR 2023）论文解读_conditional position embedding (cpe)-CSDN博客），这里就不需要再额外显式添加位置编码了。另外和传统的transformer block一样，这里还使用了FFN、LayerNorm以及skip-connection。

基于MaxViT block，作者构建了MaxViT网络，如下所示

不同尺寸的模型variant参数配置如下表所示

实验结果

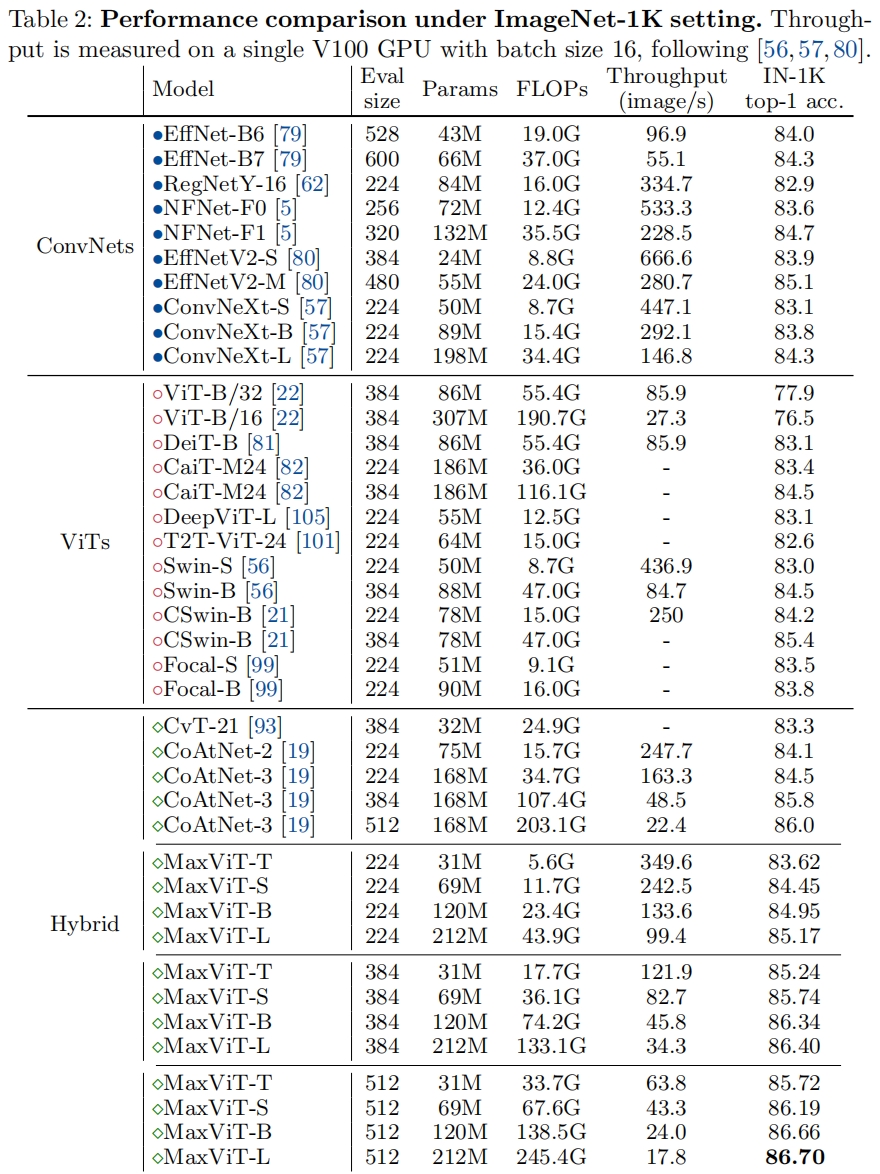
和其它SOTA模型在ImageNet-1k上的性能对比如下表所示。不过好像是在增加参数量减慢推理速度的前提下提升的精度，比如在224的输入下，MaxViT-S和Swin-S精度对比是84.45% vs. 83.0%，但同时吞吐小了一倍 242.5 vs. 436.9。

代码解析

这里以timm中的实现为例，模型选择"maxxvit_rmlp_small_rw_256"，输入大小为(1, 3, 224, 224)。这里的创新点主要是图3中的Window Partition和Grid Partition，按图3的方式划分同一颜色的像素并取出相同颜色的像素放到同一维度，后续计算self-attention就是普通的实现。

window_partition、window_reverse、grid_partition、grid_reverse的实现如下

def window_partition(x, window_size: List[int]):
    B, H, W, C = x.shape  # 1,64,64,96
    _assert(H % window_size[0] == 0, f'height ({H}) must be divisible by window ({window_size[0]})')
    _assert(W % window_size[1] == 0, '')
    x = x.view(B, H // window_size[0], window_size[0], W // window_size[1], window_size[1], C)  # (1,8,8,8,8,96)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size[0], window_size[1], C)  # (64,8,8,96)
    return windows


@register_notrace_function  # reason: int argument is a Proxy
def window_reverse(windows, window_size: List[int], img_size: List[int]):  # (64,8,8,96), (8,8)
    H, W = img_size
    C = windows.shape[-1]
    x = windows.view(-1, H // window_size[0], W // window_size[1], window_size[0], window_size[1], C)  # (1,8,8,8,8,96)
    x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, H, W, C)  # (1,64,64,96)
    return x


def grid_partition(x, grid_size: List[int]):  # (1,64,64,96), (8,8)
    B, H, W, C = x.shape
    _assert(H % grid_size[0] == 0, f'height {H} must be divisible by grid {grid_size[0]}')
    _assert(W % grid_size[1] == 0, '')
    x = x.view(B, grid_size[0], H // grid_size[0], grid_size[1], W // grid_size[1], C)  # (1,8,8,8,8,96)
    windows = x.permute(0, 2, 4, 1, 3, 5).contiguous().view(-1, grid_size[0], grid_size[1], C)  # (64,8,8,96)
    return windows


@register_notrace_function  # reason: int argument is a Proxy
def grid_reverse(windows, grid_size: List[int], img_size: List[int]):
    H, W = img_size
    C = windows.shape[-1]
    x = windows.view(-1, H // grid_size[0], W // grid_size[1], grid_size[0], grid_size[1], C)
    x = x.permute(0, 3, 1, 4, 2, 5).contiguous().view(-1, H, W, C)
    return x

我们来验证一下window_partition和grid_partition，首先是widow_partition，代码如下

import torch


def window_partition(x, window_size):
    B, H, W, C = x.shape  # 1,64,64,96
    x = x.view(B, H // window_size[0], window_size[0], W // window_size[1], window_size[1], C)  # (1,8,8,8,8,96)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size[0], window_size[1], C)  # (64,8,8,96)
    return windows


# 定义张量的形状
B, H, W, C = 1, 64, 64, 1
grid_size = (8, 8)
num_grids = (H // grid_size[0]) * (W // grid_size[1])

# 创建一个包含格子索引的张量
indices = torch.arange(1, num_grids + 1).view(H // grid_size[0], W // grid_size[1])

# 将索引张量扩展到每个格子中的所有值
indices = indices.repeat_interleave(grid_size[0], dim=0).repeat_interleave(grid_size[1], dim=1)

# 添加批次和通道维度
indices = indices.unsqueeze(0).unsqueeze(-1)

print(indices.shape)  # (1,64,64,1)
# print(indices)

print(indices[0, :9, :9, 0])
# tensor([[ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 1,  1,  1,  1,  1,  1,  1,  1,  2],
#         [ 9,  9,  9,  9,  9,  9,  9,  9, 10]])
print(indices[0, 8:16, 8:16, 0])
# tensor([[10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10],
#         [10, 10, 10, 10, 10, 10, 10, 10]])

windows = window_partition(indices, (8, 8))
print(windows.shape)  # (64,8,8,1)
print(windows[0, ..., 0])
# tensor([[1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1]])
print(windows[1, ..., 0])
# tensor([[2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2]])
print(windows[10, ..., 0])
# tensor([[11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11]])

然后再验证下grid_partition

import torch


def grid_partition(x, grid_size):  # (1,64,64,96), (8,8)
    B, H, W, C = x.shape
    x = x.view(B, grid_size[0], H // grid_size[0], grid_size[1], W // grid_size[1], C)  # (1,8,8,8,8,96)
    windows = x.permute(0, 2, 4, 1, 3, 5).contiguous().view(-1, grid_size[0], grid_size[1], C)  # (64,8,8,96)
    return windows


# 定义张量的形状
B, H, W, C = 1, 64, 64, 1
grid_size = (8, 8)

# 初始化一个空张量
tensor = torch.zeros((B, H, W, C), dtype=torch.int32)

# 填充张量
for i in range(H // grid_size[0]):
    for j in range(W // grid_size[1]):
        # 计算当前格子的起始和结束索引
        start_i, end_i = i * grid_size[0], (i + 1) * grid_size[0]
        start_j, end_j = j * grid_size[1], (j + 1) * grid_size[1]

        # 填充当前格子的值
        tensor[0, start_i:end_i, start_j:end_j, 0] = torch.arange(1, grid_size[0] * grid_size[1] + 1).view(grid_size)


print(tensor.shape)  # (1,64,64,1)
# print(tensor)

print(tensor[0, :9, :9, 0])
# tensor([[ 1,  2,  3,  4,  5,  6,  7,  8,  1],
#         [ 9, 10, 11, 12, 13, 14, 15, 16,  9],
#         [17, 18, 19, 20, 21, 22, 23, 24, 17],
#         [25, 26, 27, 28, 29, 30, 31, 32, 25],
#         [33, 34, 35, 36, 37, 38, 39, 40, 33],
#         [41, 42, 43, 44, 45, 46, 47, 48, 41],
#         [49, 50, 51, 52, 53, 54, 55, 56, 49],
#         [57, 58, 59, 60, 61, 62, 63, 64, 57],
#         [ 1,  2,  3,  4,  5,  6,  7,  8,  1]], dtype=torch.int32)
print(tensor[0, 8:16, 8:16, 0])
# tensor([[ 1,  2,  3,  4,  5,  6,  7,  8],
#         [ 9, 10, 11, 12, 13, 14, 15, 16],
#         [17, 18, 19, 20, 21, 22, 23, 24],
#         [25, 26, 27, 28, 29, 30, 31, 32],
#         [33, 34, 35, 36, 37, 38, 39, 40],
#         [41, 42, 43, 44, 45, 46, 47, 48],
#         [49, 50, 51, 52, 53, 54, 55, 56],
#         [57, 58, 59, 60, 61, 62, 63, 64]], dtype=torch.int32)

windows = grid_partition(tensor, (8, 8))
print(windows.shape)  # (64,8,8,1)
print(windows[0, ..., 0])
# tensor([[1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1],
#         [1, 1, 1, 1, 1, 1, 1, 1]], dtype=torch.int32)
print(windows[1, ..., 0])
# tensor([[2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2],
#         [2, 2, 2, 2, 2, 2, 2, 2]], dtype=torch.int32)
print(windows[10, ..., 0])
# tensor([[11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11],
#         [11, 11, 11, 11, 11, 11, 11, 11]], dtype=torch.int32)