Swin Transformer（ICCV 2021）论文与代码解析

paper：Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

official implementation：https://github.com/microsoft/Swin-Transformer

third-party implementation：https://github.com/huggingface/pytorch-image-models/blob/main/timm/models/swin_transformer.py

存在的问题

将Transformer应用于视觉任务时遇到的一些关键问题包括：

1. 计算复杂度高：传统的全局自注意力机制导致计算复杂度随着输入图像大小的增加呈二次方增长。
2. 缺乏多尺度建模能力：视觉任务需要在不同尺度上进行建模，而传统的Transformer架构在这方面存在局限。

本文的创新点

1. 层次化Transformer结构：Swin Transformer 构建了一个层次化的表示，通过逐渐合并图像块来创建不同尺度的特征图。
2. Shifted Window机制：引入了Shifted Windows机制，通过限制在非重叠的局部窗口内进行自注意力计算，同时允许跨窗口连接，从而提高计算效率和模型的全局建模能力。

优点

1. 线性计算复杂度：通过局部窗口自注意力机制，Swin Transformer将计算复杂度从输入图像大小的二次方降低为线性，从而在处理高分辨率图像时更加高效。
2. 通用性强：Swin Transformer 的设计使其能够适应不同的视觉任务，如图像分类、目标检测和语义分割。
3. 高性能：
   图像分类：在ImageNet-1K数据集上实现了87.3%的Top-1准确率。
   目标检测：在COCO test-dev数据集上取得了58.7的Box AP和51.1的Mask AP，分别比之前的最优结果高出2.7和2.6。
   语义分割：在ADE20K val数据集上实现了53.5的mIoU，比之前的最优结果高出3.2

方法介绍

Overall Architecture

Swin Transformer的整体结构如图3所示。和ViT一样，输入首先通过一个patch splitting module分割成若干重叠的patch。每个patch都作为一个token。本文采用4x4的patch大小，因此每个patch的特征维度是4x4x3=48。然后通过一个linear embedding层将特征维度映射为 \(C\)。

然后是若干个swin transformer block，其中包含了本文改进后的self-attention。transformer block保持了token的数量（\(\frac{H}{4}\times \frac{W}{4}\)），和前面的线性embedding层一起组成了“Stage 1”。

为了得到层次化的表示，随着网络的深度，我们通过patch merging layer来减少token的数量。第一个patch merging层将相邻的2x2个patch拼接起来，得到特征维度为 \(4C\) 的输出，然后经过一个linear layer将特征维度映射到 \(2C\)。这一步将token数量减少了2x2=4倍（分辨率降采样2倍），输出特征维度变为了 \(2C\)。后就是若干个swin transformer block，其中分辨率保持 \(\frac{H}{8}\times \frac{W}{8}\)。patch merging层和后续的swin transformer block组成了“Stage 2”。这一过程再重复两次得到“Stage 3”和“Stage 4”，对应的输出分辨率分别为 \(\frac{H}{16}\times \frac{W}{16}\) 和 \(\frac{H}{32}\times \frac{W}{32}\)。

Swin Transformer block Swin Transformer是通过将标准的多头自注意力（MSA）替换为一个基于移动窗口的模块来构建的，其它层保持不变。如图3(b)所示，一个Swin Transformer block包含一个基于移动窗口的MSA模块，然后两层的MLP其中激活函数是GELU。每个MSA和MLP之前都有一个LayerNorm，并且每个模块后都应用了residual connection。

Shifted Window based Self-Attention

在标准的transformer结构中需要计算全局self-attention，即需要计算每个token和其它所有token之间的关系。这导致了复杂度是token数量二次方，不适用于需要大量token来进行密集预测或需要高分辨率输入图像的视觉任务。

Self-attention in non-overlapped windows 为了有效的建模，本文提出在局部窗口内计算自注意力。这些窗口以不重叠的方式均匀地切分图像。假设每个窗口包含 \(M\times M\) 个patch，对一个有 \(h\times w\) 个patch的输入图像，全局MSA和基于窗口的MSA的计算复杂度分别为

其中前者和patch数量 \(hw\) 呈二次方关系，后者当 \(M\) 是固定值时（默认设置为7）呈线性关系。

Shifted window partitioning in successive blocks 基于窗口的自注意力模块缺乏跨窗口的连接，限制了其建模能力。为了保持非重叠窗口计算效率的同时引入跨窗口连接，作者提出了一种移动窗口划分方法，在连续的Swin Transformer block中交替使用两种划分配置。

如图2所示，第一个模块使用常规的窗口划分策略，从左上角像素开始，8x8的特征图被均匀地划分成了2x2=4个窗口（每个窗口的大小为4x4，即M=4）。然后下一个模块采用一个移动窗口的配置，将常规的窗口移动\((\left \lfloor \frac{M}{2} \right \rfloor ,\left \lfloor \frac{M}{2} \right \rfloor)\) 个像素。则连续的两个swin transformer block的计算如下

Efficient batch computation for shifted configuration 移动窗口划分的一个问题是它会得到更多的窗口，从 \(\left \lceil \frac{h}{M} \right \rceil \times \left \lceil \frac{w}{M} \right \rceil \) 到 \((\left \lceil \frac{h}{M} \right \rceil+1) \times (\left \lceil \frac{w}{M} \right \rceil+1) \)，并且一个窗口会小于 \(M\times M\)。一个容易想到的解决方法是将较小的窗口填充到 \(M\times M\) 大小，并在计算注意力时屏蔽填充的值。当常规划分的窗口数量很小比如2x2时，这种方法增加的计算量非常大（2x2 -> 3x3，是原来的2.25倍）。这里作者提出了一种更有效的batch计算方法，将向左上角循环移位，如图4所示。

这样移动以后，一个batch的窗口可能由若干在特征图中不相邻的窗口组成，然后通过mask机制将自注意的计算限制在每个子窗口内。通过循环移位的方式，处理的窗口数量和常规划分方式相等，从而更加高效。

Relative position bias 本文的位置编码是通过在计算自注意时，在每个头内计算相似度时引入一个相对位置偏差 \(B\in \mathbb{R}^{M^2 \times {M^2}}\) 来实现的

其中 \(Q,K,V\in \mathbb{R}^{M^2\times d}\) 是query、key和value矩阵，\(d\) 是query和key的维度，\(M^2\) 是窗口内patch的数量。由于沿每个轴的相对位置都在 \([-M+1,M-1]\) 范围内，我们参数化了一个小的bias矩阵 \(\hat{B}\in \mathbb{R}^{(2M-1)\times (2M-1)}\)，\(B\) 中的值是从 \(\hat{B}\) 中取的。

作者通过实验观察到与不用这个bias项或使用绝对位置相比，relative bias有显著的改进。进一步向输入添加ViT中的绝对位置编码也会导致性能略微下降，因此本文没有采用它。

在预训练中学习到的相对位置偏差也可以通过bi-cubic插值来初始化一个具有不同窗口大小的微调模型。

Architecture Variant

作者构建了Swin-B，该模型具有类似于ViT-B/DeiT-B的模型大小和计算复杂度。此外还构建了Swin-T、Swin-S、Swin-L，它们分别是模型大小和复杂度为0.25x、0.5x、2x的版本。需要注意的是，Swin-T和Swin-S的复杂度分别与ResNet-50（DeiT-S）和ResNet-101相似。窗口大小默认为M=7，每个head的query维度为d=32，每个MLP的expansion ratio为 \(\alpha=4\)。各个变体的超参如下

详细的模型结构配置如下所示，其中"concat nxn"表示将相邻的nxn个特征拼接到一个patch中，即patch merging层，这一层将特征图降采样n倍。

实验结果 

与其它模型在ImageNet上的结果如表1所示。其中表1(a)是常规的ImageNet-1K从头训练的结果，可以看到超过了之前基于transformer的sota模型DeiT，比如在相近的复杂度下，Swin-T（81.3%）超过了DeiT-T（79.8）1.5%，当输入大小分别为224x224/384x384时，Swin-B（83.3%/84.5%）分别超过了DeiT-B（81.8%/83.1%）1.5%/1.4%。与基于卷积的sota模型比如RegNet和EfficientNet相比时，Swin Transformer也获得了更好的速度-精度的平衡。

表1(b)是在ImageNet-22K上对更大的Swin-B和Swin-L进行预训练后在ImageNet-1K上微调的结果，对于Swin-B，和在ImageNet-1K上从头训练相比，在ImageNet-22K上预训练然后微调提升了1.8%~1.9%。和之前预训练的sota相比，Swin-B（86.4%）超过了ViT-B 2.4%。

在COCO目标检测模型的结果对别如下表所示

代码解析

这里以timm中的实现为例进行讲解。模型选择“swin_small_patch4_window7_224”，输入大小为 (1, 3, 224, 224)。 

在函数forward_features中首先调用self.patch_embed，这里patch_size=4，输出通道为96，类PatchEmbed的实现中去掉那些花里胡哨的东西就是一个卷积 Conv2d(3, 96, kernel_size=(4, 4), stride=(4, 4))，经过这一步得到输出(1, 56, 56, 96)。

然后就是多个SwinTransformerStage，除了第一个stage，剩余的所有stage中的SwinTransformerStage一开始都需要进行downsample，具体通过patchmerging实现，其实就是yolov5中的focus层，沿spatial维度跨stride取值然后再沿通道维度concat，比如stride=2时分辨率下采样2倍则通道数变成原来的4倍。

class PatchMerging(nn.Module):
    """ Patch Merging Layer.
    """

    def __init__(
            self,
            dim: int,
            out_dim: Optional[int] = None,
            norm_layer: Callable = nn.LayerNorm,
    ):
        """
        Args:
            dim: Number of input channels.
            out_dim: Number of output channels (or 2 * dim if None)
            norm_layer: Normalization layer.
        """
        super().__init__()
        self.dim = dim
        self.out_dim = out_dim or 2 * dim
        self.norm = norm_layer(4 * dim)
        self.reduction = nn.Linear(4 * dim, self.out_dim, bias=False)

    def forward(self, x):
        B, H, W, C = x.shape
        _assert(H % 2 == 0, f"x height ({H}) is not even.")
        _assert(W % 2 == 0, f"x width ({W}) is not even.")
        x = x.reshape(B, H // 2, 2, W // 2, 2, C).permute(0, 1, 3, 4, 2, 5).flatten(3)
        x = self.norm(x)
        x = self.reduction(x)
        return x

然后调用SwinTransformerBlock，在一个stage中，W-MSA和SW-MSA交替，在函数_attn中，首先进行cyclic shift，其中self.shift_size默认为7。

shifted_x = torch.roll(x, shifts=(-self.shift_size[0], -self.shift_size[1]), dims=(1, 2))  # (1,56,56,96)

关于torch.roll部分，引用一下这篇文章中的图示，https://zhuanlan.zhihu.com/p/627485931，这样过程看起来就比较清晰了

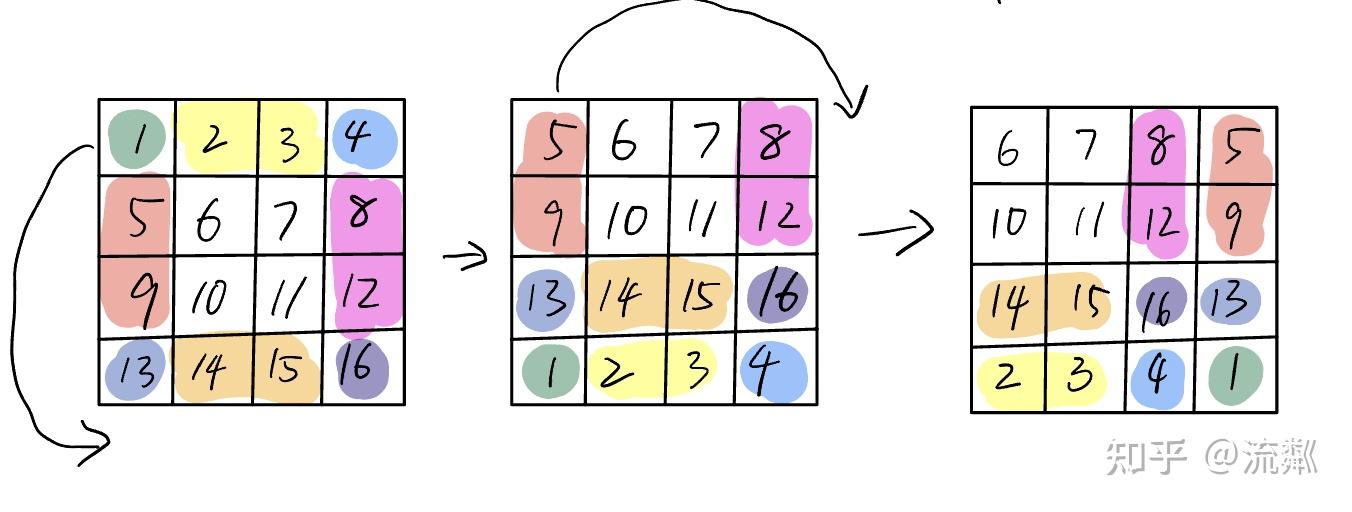
cyclic shift之后，就需要划分window，后续计算attention是在每个window内部进行的 

def window_partition(
        x: torch.Tensor,
        window_size: Tuple[int, int],
) -> torch.Tensor:
    """
    Partition into non-overlapping windows with padding if needed.
    Args:
        x (tensor): input tokens with [B, H, W, C].
        window_size (int): window size.

    Returns:
        windows: windows after partition with [B * num_windows, window_size, window_size, C].
        (Hp, Wp): padded height and width before partition
    """
    B, H, W, C = x.shape
    x = x.view(B, H // window_size[0], window_size[0], W // window_size[1], window_size[1], C)  # (1,56,56,96)->(1,8,7,8,7,96)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size[0], window_size[1], C)  # (1,8,8,7,7,96)->(64,7,7,96)
    return windows

对于上面的图示，按下图均分的方式切分window，图中的patch其实指的是window，在window的内部又划分为多个patch。

然后就是在每个window内部计算attention，因为cyclic shift后每个window内部可能包含多个不同的sub window，因此在计算attention时就需要通过mask屏蔽掉不属于同一个子窗口的信息，比如上图右下角有16、13、4、1四个子窗口，在计算attention时屏蔽掉13,4,1的信息就相当于只在子窗口16内部计算注意力，计算其它子窗口时也类似，这样就保证了只在每个子窗口内计算注意力。

mask的计算如下，这里是将每个子窗口按索引赋值，比如上图按颜色共有9个子窗口，分别赋值0-8。

if any(self.shift_size):
    # calculate attention mask for SW-MSA
    H, W = self.input_resolution  # (56,56)
    H = math.ceil(H / self.window_size[0]) * self.window_size[0]  # 56
    W = math.ceil(W / self.window_size[1]) * self.window_size[1]  # 56
    img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
    cnt = 0
    for h in (
            slice(0, -self.window_size[0]),  # (0, -7)
            slice(-self.window_size[0], -self.shift_size[0]),  # (-7, -3)
            slice(-self.shift_size[0], None)):  # (-3, None)
        for w in (
                slice(0, -self.window_size[1]),  # (0, -7)
                slice(-self.window_size[1], -self.shift_size[1]),  # (-7, -3)
                slice(-self.shift_size[1], None)):  # (-3, None)
            img_mask[:, h, w, :] = cnt
            cnt += 1
    mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1, (1,56,56,1)->(64,7,7,1)
    mask_windows = mask_windows.view(-1, self.window_area)  # (64,49)
    # print(torch.unique(mask_windows))
    attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)  # (64,1,49)-(64,49,1)->(64,49,49)
    # print(torch.unique(attn_mask))
    attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
    # print(attn_mask.shape)
    # print(torch.unique(attn_mask))
    # exit()

同样还是这个作者的图示，最右一列是注意力权重的计算结果，其中只保留带颜色的位置的结果，即左侧同一颜色（同一sub window）的计算结果，其余×的位置设置为一个很小的数，代码中是-100。因为mask是与 \(qk^T\) 的结果相加而不是相乘，后面再计算softmax时很小的负值就变成了0。代码如下

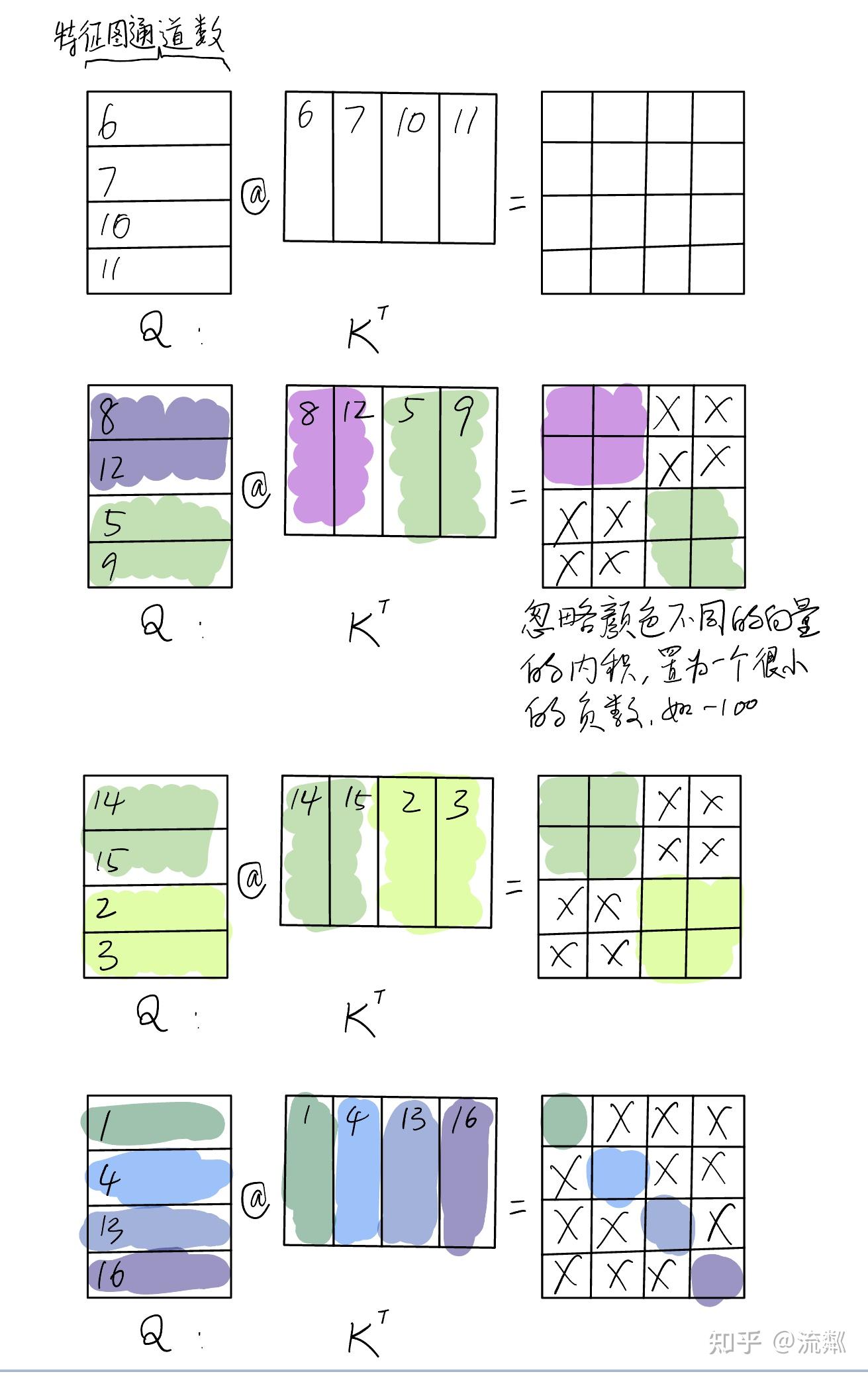
q = q * self.scale
attn = q @ k.transpose(-2, -1)  # (64,3,49,49)
attn = attn + self._get_rel_pos_bias()
if mask is not None:
    num_win = mask.shape[0]
    attn = attn.view(-1, num_win, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
    attn = attn.view(-1, self.num_heads, N, N)
attn = self.softmax(attn)
attn = self.attn_drop(attn)
x = attn @ v

最后要说的是位置编码，这里采用的是相对位置偏差，而不是ViT中的绝对位置编码，且这里的偏差是网络学习得到的，偏差的定义如下。本文所有stage的窗口大小都是7x7，这里定义的张量大小为(13, 13, num_heads)，这是因为沿x和y方向的相对位置偏差各自最多只有13种情况。比如以x轴为例，第一个像素x=0，最后一个像素x=6，这里要考虑前后相对位置，因此有0-6=-6和6-0=6两种情况，再加上相对偏差为0，共有6+6+1=13种情况。同样y轴也有13种情况，因此共有13x13=169种情况。

# define a parameter table of relative position bias, shape: 2*Wh-1 * 2*Ww-1, nH
self.relative_position_bias_table = nn.Parameter(torch.zeros((2 * win_h - 1) * (2 * win_w - 1), num_heads))  # (169,3), 2*7-1=13

然后是定义了一个相对坐标索引的表，注意这张表是两个像素点之间坐标的偏差，比如(0, 1)和(3, 5)沿x方向偏差了3个像素，沿y方向偏差了4个像素，但模型中实际与attention相加的不是这张表，而是上面学习的那张表。这张表的作用是为了坐标偏差相同的像素pair之间的bias也是相同的，比如(0, 1)和(3, 5)与(2, 4)和(5, 8)这两对像素点之间的bias是相同的，而bias具体的值是网络学习得到的。

其中39-40两行的作用让坐标的偏移量从0开始，上面提到过偏差是[-M+1, M-1]即[-6, 6]，这里将这个范围平移到[0, 12]，是因为后续要用relative_position_index这张表里的值当做索引从relative_position_bias_table这张表取具体的bias，而索引不能为负值。

42行的作用是因为最后返回时将xy的偏差加到一起，而(0, 1)和(1, 0)相加后都为1就无法区分开了，将x的偏差都乘以13后就可以区分开了。

# get pair-wise relative position index for each token inside the window
self.register_buffer("relative_position_index", get_relative_position_index(win_h, win_w), persistent=False)

def get_relative_position_index(win_h: int, win_w: int):  # 7,7
    # get pair-wise relative position index for each token inside the window
    coords = torch.stack(ndgrid(torch.arange(win_h), torch.arange(win_w)))  # 2, Wh, Ww
    # (2,7,7)
    # tensor([[[0, 0, 0, 0, 0, 0, 0],
    #          [1, 1, 1, 1, 1, 1, 1],
    #          [2, 2, 2, 2, 2, 2, 2],
    #          [3, 3, 3, 3, 3, 3, 3],
    #          [4, 4, 4, 4, 4, 4, 4],
    #          [5, 5, 5, 5, 5, 5, 5],
    #          [6, 6, 6, 6, 6, 6, 6]],
    #
    #         [[0, 1, 2, 3, 4, 5, 6],
    #          [0, 1, 2, 3, 4, 5, 6],
    #          [0, 1, 2, 3, 4, 5, 6],
    #          [0, 1, 2, 3, 4, 5, 6],
    #          [0, 1, 2, 3, 4, 5, 6],
    #          [0, 1, 2, 3, 4, 5, 6],
    #          [0, 1, 2, 3, 4, 5, 6]]])
    coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
    # (2,49)
    # tensor([[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3,
    #          3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6,
    #          6],
    #         [0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2,
    #          3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5,
    #          6]])
    relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
    # (2,49,1)-(2,1,49)->(2,49,49), 先y坐标后x坐标，先行后列的顺序，每个点与其它所有点y和x的相对坐标
    relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
    # (49,49,2), 按先行后列的顺序，每个点与其它所有点的(rel_y, rel_x)
    # 前两个点和其它所有点的相对坐标差
    # [[[0, 0], [0, -1], [0, -2], [0, -3], [0, -4], [0, -5], [0, -6], [-1, 0], [-1, -1], [-1, -2], [-1, -3], [-1, -4], [-1, -5], [-1, -6], [-2, 0], [-2, -1], [-2, -2], [-2, -3], [-2, -4], [-2, -5], [-2, -6], [-3, 0], [-3, -1], [-3, -2], [-3, -3], [-3, -4], [-3, -5], [-3, -6], [-4, 0], [-4, -1], [-4, -2], [-4, -3], [-4, -4], [-4, -5], [-4, -6], [-5, 0], [-5, -1], [-5, -2], [-5, -3], [-5, -4], [-5, -5], [-5, -6], [-6, 0], [-6, -1], [-6, -2], [-6, -3], [-6, -4], [-6, -5], [-6, -6]],
    # [[0, 1], [0, 0], [0, -1], [0, -2], [0, -3], [0, -4], [0, -5], [-1, 1], [-1, 0], [-1, -1], [-1, -2], [-1, -3], [-1, -4], [-1, -5], [-2, 1], [-2, 0], [-2, -1], [-2, -2], [-2, -3], [-2, -4], [-2, -5], [-3, 1], [-3, 0], [-3, -1], [-3, -2], [-3, -3], [-3, -4], [-3, -5], [-4, 1], [-4, 0], [-4, -1], [-4, -2], [-4, -3], [-4, -4], [-4, -5], [-5, 1], [-5, 0], [-5, -1], [-5, -2], [-5, -3], [-5, -4], [-5, -5], [-6, 1], [-6, 0], [-6, -1], [-6, -2], [-6, -3], [-6, -4], [-6, -5]],
    # ...
    relative_coords[:, :, 0] += win_h - 1  # shift to start from 0
    relative_coords[:, :, 1] += win_w - 1
    # 上面两行让值大于0是因为这里的值后续要作为索引从relative_position_bias_table里面取值
    relative_coords[:, :, 0] *= 2 * win_w - 1  # x坐标乘以2*win_w-1一是为了让下面一行xy坐标相加得到的值是唯一的，防止把(0,1)和(1,0)相加都等于1这种情况
    # 至于具体乘的值选择2*win_w-1是因为有x方向有2*win_w-1种情况
    return relative_coords.sum(-1)  # Wh*Ww, Wh*Ww

在计算attention中，将学习到的bias与 \(qk^T\) 相加，然后用mask处理，最后再计算softmax并与 \(v\) 相乘。注意这里和ViT中绝对位置编码的区别，这里是与attention相加，且每个transformer block中计算注意力时都要加一次。在ViT中的绝对位置编码是在进入block前与输入相加，且只需要加一次就可以了。

attn = attn + self._get_rel_pos_bias()

def _get_rel_pos_bias(self) -> torch.Tensor:
    relative_position_bias = self.relative_position_bias_table[
        self.relative_position_index.view(-1)].view(self.window_area, self.window_area, -1)  # Wh*Ww,Wh*Ww,nH
    relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww
    return relative_position_bias.unsqueeze(0)