信息熵及其相关概念

息论的核心思想是量化数据中的信息内容。

1. 熵的定义

信息熵的定义公式：
$$H(X)=-\sum _{x\in X}p(x)\log p(x)$$
并且规定 0 log (0) = 0

信息论的基本定理之一指出，为了对从X所在的分布 p 中随机抽取的数据进行编码，我们至少需要 H[X] “纳特（nat）” 对其进行编码。

1.1 信息熵的三个性质

信息论之父克劳德·香农给出的信息熵的三个性质[1]：

1. 单调性，发生概率越高的事件，其携带的信息量越低；
2. 非负性，信息熵可以看作为一种广度量，非负性是一种合理的必然；
3. 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和，这也是广度量的一种体现。

香农从数学上严格证明了满足上述三个条件的随机变量不确定性度量函数具有唯一形式
$$H(X)=-C\sum _{x\in X}p(x)\log p(x)$$
其中的 C CC 为常数，我们将其归一化为 C = 1 C=1C=1 即得到了信息熵公式。

1.2 对信息熵三条性质的理解

• 单调性说的是，事件发生的概率越低，其发生时所能给出的信息量越大。
  举一个极端的例子，“太阳从西边升起”所携带的信息量就远大于“太阳从东边升起”，因为后者是一个万年不变的事实，不用特意述说大家都知道；而前者是一个相当不可能发生的事情，如果发生了，那代表了太多的可能性，可能太阳系有重大变故，可能物理法则发生了变化，等等。
  从某种角度来考虑，单调性也暗含了一种对信息含量的先验假设，即默认某些事实是不含信息量的（默认事实其实也是一种信息，我理解的默认事实应该指的是概率分布），这其实是把默认情况的信息量定标为 0 了。

• 非负性显然成立$H(X)\ge 0$

• 对累加性的解释，考虑到信息熵的定义涉及到了事件发生的概率，我们可以假设信息熵是事件发生概率的函数：
  $$H(X)=H(p(x))$$
  对于两个相互独立的事件 X = A , Y = B 来说，其同时发生的概率：
  $$p(X=A,Y=B)=p(X=A)\cdot p(Y=B)$$
  其同时发生的信息熵，根据累加性可知：

$$H(p(X=A,Y=B))=H(p(X=A)\cdot p(Y=B))=H(p(X=A))+H(p(Y=B))$$

一种函数形式，满足两个变量乘积函数值等于两个变量函数值的和，那么这种函数形式应该是对数函数。

2. 伯努利分布熵的计算

熵的定义公式中对数函数不局限于采用特定的底，不同的底对应了熵的不同度量单位。

• 如果以 2 为底，熵的单位称作比特 (bit)；
• 如果以自然对数 e 为底，熵的单位称作纳特 (nat)。

从熵的定义中可以看出，熵是关于变量 X 概率分布的函数，而与 X 的取值没有关系，所以也可以将 X 的熵记作 H ( p )

熵越大代表随机变量的不确定性越大，当变量可取值的种类一定时，其取每种值的概率分布越平均，其熵值越大。熵的取值范围为：
$$0\le H(p)\le log(n)$$
n 表示取值的种类。

当随机变量只取两个值，例如 1 11，0 00 时，即 X 的分布为：
$$P(X=1)=p,P(X=0)=1-p,0\le p\le 1$$
熵为：
$$H(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p)$$
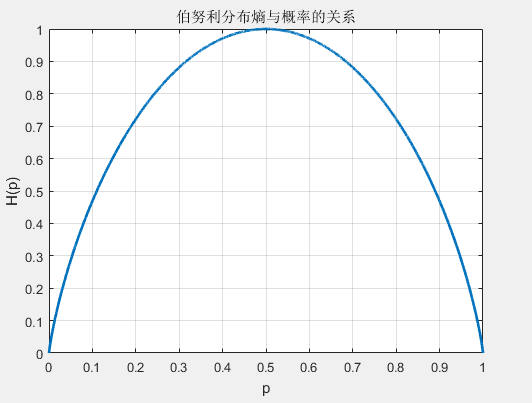
这时，熵 H ( P ) 随概率 p 变化的曲线如下图所示（单位为比特），

当 p = 0 或 p = 1 时， H ( p ) = 0 ，随机变量完全没有不确定性。
当 p = 0.5 时，H ( p ) = 1 ， 熵取值最大，随机变量不确定性最大。

3. 两随机变量系统中熵的相关概念

3.1 联合熵

两个离散随机变量 X 和 Y 的联合熵 (Joint Entropy) 为：
$$H(X,Y)=-\sum _{y\in Y}\sum _{x\in X}p(x,y)\log p(x,y)$$

联合熵表征了两事件同时发生系统的不确定度。

3.2 条件熵

条件熵 (Conditional Entropy) H ( Y ∣ X ) 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。

$$H(Y\mid X)=\sum _{x\in X}p(x)H(Y\mid x)=-\sum _{x\in X}p(x)\sum _{y\in Y}p(y\mid x)\log p(y\mid x)$$

3.3 互信息

两个离散随机变量 X 和 Y 的互信息 (Mutual Information) 定义为：

$$I(X,Y)=\sum _{y\in Y}\sum _{x\in X}p(x,y)\log (\frac{p(x)p(y)}{p(x,y)})$$

为了理解互信息的涵义，我们把公式中的对数项分解:

$$\begin{gathered} \log (\frac{p(x)p(y)}{p(x,y)}) \\ =\log p(x,y)-(\log p(x)+\log p(y)) \\ =-\log p(x)-\log p(y)-(-\log p(x,y)) \end{gathered}$$

上式表明，两事件的互信息为各自事件单独发生所代表的信息量之和减去两事件同时发生所代表的信息量之后剩余的信息量，这表明了两事件单独发生给出的信息量之和是有重复的，互信息度量了这种重复的信息量大小。

最后再求概率和表示了两事件互信息量的期望。从式中也可以看出，当两事件完全独立时，p ( x , y ) = p ( x ) ⋅ p ( y ) ，互信息计算为 0 ，这也是与常识判断相吻合的。

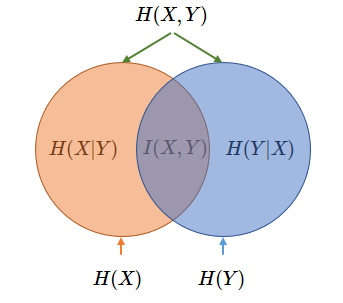
3.4 互信息、联合熵、条件熵之间的关系

$$\begin{gathered} I(X,Y)=H(X)+H(Y)-H(X,Y) \\ =H(Y)-H(Y|X)=H(X)-H(X|Y) \\ =H(X,Y)-H(Y|X)-H(X|Y) \end{gathered}$$

另外，在分类任务的决策树学习过程中，采用信息增益的概念来决定选用哪个特征作为后续的决策依据。这里的信息增益等价于训练数据集中类与特征的互信息。

4. 两分布系统中熵的相关概念

4.1 交叉熵

考虑一种情况，对于一个样本集，存在两个概率分布 p ( x ) ) 和 q ( x ) ，其中 p ( x ) 为真实分布，q ( x ) 为非真实分布。

基于真实分布 p ( x ) 我们可以计算这个样本集的信息熵也就是编码长度的期望为：
$$H(p)=-\sum _{x}p(x)\log p(x)$$

如果我们用非真实分布 q ( x ) 来代表样本集的信息量的话，那么：
$$H(p,q)=-\sum _{x}p(x)\log q(x)$$

因为其中表示信息量的项来自于非真实分布 q ( x )，而对其期望值的计算采用的是真实分布 p ( x ) ，所以称其为交叉熵 (Cross Entropy)。

交叉熵比原本真实的信息熵要大。直观来看，当我们对分布估计不准确时，总会引入额外的不必要信息期望（可以理解为引入了额外的偏差），再加上原本真实的信息期望，最终的信息期望值要比真实系统分布所需的信息期望值要大。

4.2 相对熵 (KL 散度)

相对熵 (Relative Entropy) 也称 KL 散度，设 p ( x ) 、q ( x ) 是离散随机变量 X 的两个概率分布，则 p 对 q 的相对熵为：
$$D_{KL}(p||q)=\sum _{x}p(x)\log \frac{p(x)}{q(x)}$$

$D_{KL}(p\Vert q)\ge 0$

4.3 相对熵与交叉熵的关系

$$\begin{gathered} D_{KL}(p||q)=\sum _{x}p(x)\log \frac{p(x)}{q(x)} \\ =-\sum _{x}p(x)\log q(x)-(-\sum _{x}p(x)\log p(x)) \\ =H(p,q)-H(p) \end{gathered}$$

因为$D_{KL}(p\Vert q)\ge 0$，所以$H(p,q)\ge H(p)$