SVD原理以及推导
一。关于这篇文章的开始几句话
看过我之前写过文章的童鞋们会发现我写文章的水平很烂的,所以看官们见谅啊!
SVD不仅是一个数学问题,在数学问题上主要涉及矩阵的计算,矩阵已经忘记的童鞋们最好去复习一下相关知识啊。说实话我还没怎么在实际开发中用过SVD,但是SVD以前我不会,原理和推导过程还是有意思的。
引用一句流行语——没时间解释了,快上车!!!!
二。直接开始
用SVD可以很容易得到
任意矩阵的满秩分解
,用满秩分解可以对数据做压缩。可以用SVD来证明对任
意M*N的矩阵均存在如下分解: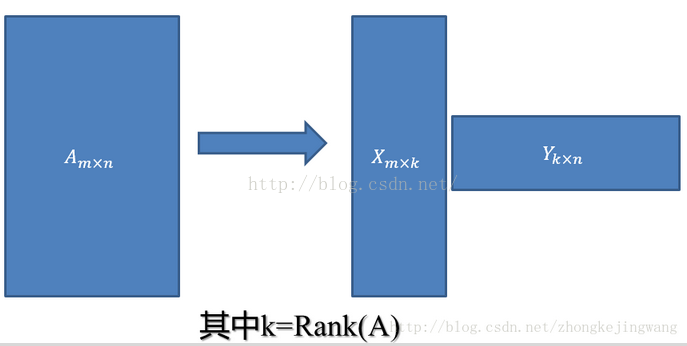

在这里Rank(A)表示的是矩阵A的秩。看到高手写的文章中说:这个可以应用在数据降维压缩上!在数据相关性特别大的情况下存储X和Y矩阵比存储A矩阵占用空间更小!接下来我们来看看为什么一个矩阵A可以分解为X和Y,如果可以合理的分解,那么用来存储也就是情理之中啦。
1.首先补充下线性代数的知识
(1)正交矩阵
正交矩阵是在欧几里得空间里的叫法,在酉空间里叫酉矩阵,一个正交矩阵对应的变换叫正交变换。别问我什么是欧几里得空间!!!!
欧几里得空间:设V是实数域R上的一个线性空间,在V上定义了一个二元实函数,称为内积,记作(A,B),它具有一下性质:
(A,B) =(B,A)
(kA,B)=k(B,A)
(A+B,T) = (A,T)+(B,T)
(A,A) >= 0 当且仅当A=0时 (A,A) = 0
这里A,B,T是V中任意向量,k是任意实数,这样的线性空间V是欧几里得空间。
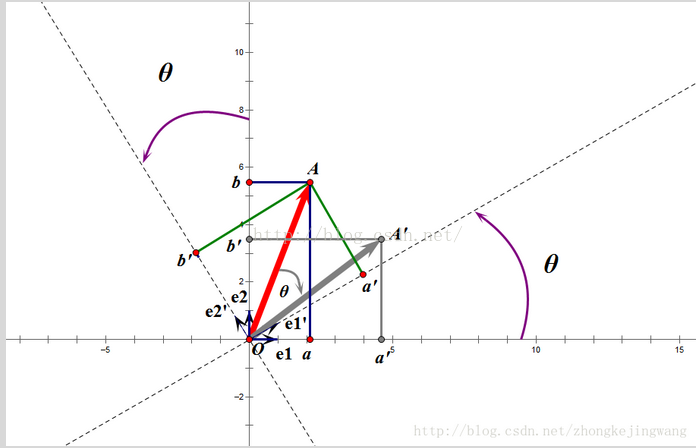
这个变换的特点是不改变向量的尺寸和向量间的夹角,那么它到底是个什么样的变换呢?看下面这张图:
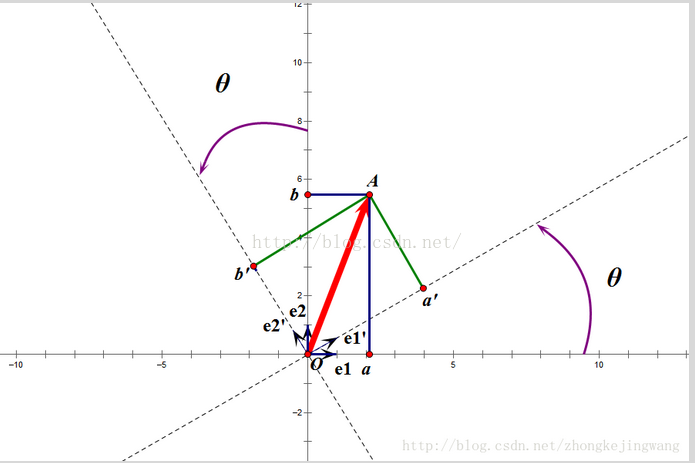
假设二维空间中的一个向量OA,它在标准坐标系(即e1、e2表示的坐标系)中表示为(a,b)'(用'表示转置),如图所示,现在把向量OA用另一组坐标e1'、e2'(在e1'和e2'表示的坐标系)表示为(a',b')',存在矩阵U使得(a',b')'=U(a,b)',则U即为正交矩阵。
这里不必纠结于(')表示的转置。在矩阵概念里,一个矩阵的转置还是矩阵,在这里只是一个示意表明不同量(a和a‘),并没有表示数值的不同或者相同。
设M是对称矩阵, P是正交矩阵, N=P'MP 称为 M的正交变换。
正交变换既是相似变换,也是相合变换。正交变换不改变M的特征值。正交变换既是相似变换,也是相合变换。正交变换不改变M的特征值。
从图中可以看到,正交变换只是将变换向量(OA)用另一组正交基表示,在这个过程中并没有对向量做拉伸,也不改变向量的空间位置。上面的例子只是正交变换的一个方面,即旋转变换,可以把e1'、e2'坐标系看做是e1、e2坐标系经过旋转SITA角度得到,怎么样得到这个神奇的旋转矩阵U呢?如下:
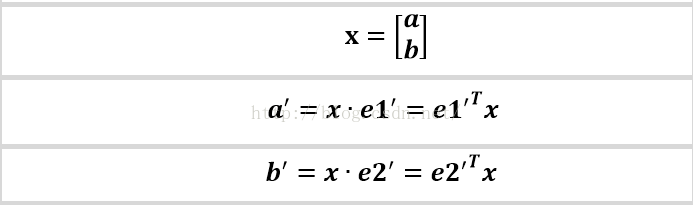
a'和b'实际上是x(就是OA啦)在e1'和e2'轴上的投影大小,所以直接做内积可得。x与e1'内积的结果就是向量 x在e1'上的投影,因为单位向量e1'的模是1啊,就是x的模乘以夹角的余弦,当然方向和e1'相同。
等式的最后面就是x*e1'的变化,结果都是相同的,同样的原因 向量e1'转置的模也是1啊。 然后:
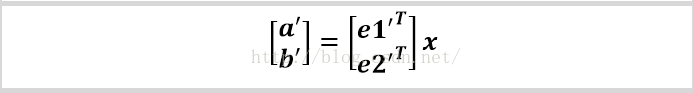
从上面的公式可以得到:
仔细看第一张图,假如e1'和e1的夹角是SITA的话,那么就有:
所以我们可以得到:
正交阵U行(列)向量之间都是单位正交向量。
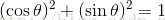
上面求得的是一个旋转矩阵,它对向量做旋转变换!也许你会有疑问:刚才不是说向量空间位置不变吗?怎么现在又说它被旋转了?对的,这两个并没有冲突,说空间位置不变是绝对的,但是坐标是相对的,加入你站在e1上看OA,随着e1旋转到e1',看OA的位置就会改变。如下图:
如图,如果我选择了e1'、e2'作为新的标准坐标系,那么在新坐标系中OA(原标








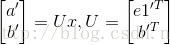

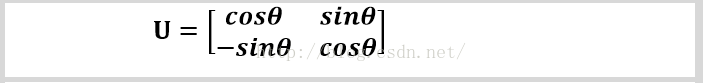
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章














 7330
7330











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








