目录
5.2、相对固定坐标系先后发生的若干运动的合成(从右向左乘)
5.3、相对运动坐标系先后发生的若干运动的合成(从左向右乘)
1、空间三维坐标系的平移(矢量加法获取)
已知P点在坐标系B中的坐标为 = (x, y, z),B坐标系相对A坐标系平移了
,求解P点在A坐标系中的坐标
。

解题思路:根据适量的加法即可求解
=
+
2、空间三维坐标系的旋转(旋转矩阵)
已知P点在坐标系B中的坐标为,B坐标系相对A坐标系任意旋转,旋转矩阵为
,求解P点在A坐标系中的坐标
。

解题思路是:
P点在B坐标系的坐标为 =
将
分解到 A 坐标的三个轴上,同理将P点在B坐标系的y,z坐标值也分解到A坐标系的三个轴上。
,
,
将所有分量在A坐标系上同一轴的分量相加可得:
因此旋转矩阵可表示为以下等式:

3、坐标系一般变换(平移+旋转)
已知P点在坐标系B中的坐标为,B坐标系相对A坐标系任意旋转+平移,旋转矩阵为
,移动向量为
,求解P点在A坐标系中的坐标
。

4、空间三维坐标系的旋转加平移,齐次变换
旋转使用矩阵乘法,平移使用矩阵加法计算,为了将旋转和平移统一成矩阵乘法的形式,将变量升维成齐次变换形式。

齐次变换矩阵的三个物理含义
4.1、坐标变换
作为两个坐标系见的坐标变换矩阵。
已知P点在B坐标轴的坐标,B坐标系以 A 坐标系为基础的相对位置和姿态,求解P点在A坐标轴的坐标。
4.2、坐标系的描述
描述坐标系B相对A的位置和姿态;
以A为基坐标轴,B坐标系原点相对A坐标系原点的位置(x,y,z);姿态(Bx在A轴三个方向投影的余弦角度;同理By;Bz等9个角度);
因为在1.1中,单独考虑旋转,定义就是B轴x坐标与A坐标系三个轴的夹角;B坐标系的y,z轴同理。
4.3、运动算子
作为运动算子来表示刚体的运动情况。
5、齐次变换矩阵乘法的物理意义

5.1、使用齐次矩阵相乘,可以时间坐标系描述之间的转换。
已知C坐标系相对B坐标系的齐次矩阵;和B坐标系相对A坐标系的齐次矩阵;求取 C 坐标系相对 A 坐标系的齐次矩阵。

5.2、相对固定坐标系先后发生的若干运动的合成(从右向左乘)

固定坐标系A;初始状态ABC坐标系重合;先将C坐标系相对B运动;再将BC相对A运动(保证BC间相对位置不变)。先运动的齐次矩阵在乘号右边。
5.3、相对运动坐标系先后发生的若干运动的合成(从左向右乘)

固定坐标系A;初始状态ABC坐标系重合;先将BC坐标系相对A运动;再将C相对B运动(保证BC间相对位置不变)。先运动的齐次矩阵在乘号左边。
6、齐次矩阵的逆变换
齐次矩阵的逆物理含义为:齐次矩阵代表B坐标系相对A坐标系的位置和姿态;逆代表A坐标系相对B坐标系的位置和姿态。


7、RPY角和欧拉角
问题:坐标系的一般变换=旋转+平移;需要 9 + 3 个变量来求解。一个三维的旋转需要使用 9 个角度的余弦求解;实际这9个余弦值只有3个是独立的,过于复杂。因此引入RPY和欧拉角的概念。
已知初始状态下,A、B两个坐标系重合,A坐标系固定不动,B坐标系进行旋转,存在两种情况:
RPY 角(固定轴):B坐标系绕A坐标的x,y,z三个轴进行旋转;固定坐标系的连续运动。
欧拉 角(运动轴):B坐标系绕B坐标的z轴旋转得到坐标系,然后绕坐标系
的y轴旋转得到坐标系
,最后然坐标系
的x轴旋转得到最终的坐标系 B。
7.1、RPY角
RPY 角(固定轴):B坐标系绕A坐标的x,y,z三个轴进行旋转;固定坐标系的连续运动。计算旋转矩阵需要使用2个知识点:
a、矩阵依旧采用第二章中旋转矩阵的形式,只是角度转动比较特殊。
b、5.2节知识,绕固定轴连续转动,采用从右向左的方向乘。
7.1.1、特殊情况,每次绕轴旋转90度角

7.1.2、一般情况,绕x轴转动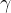 ,绕y轴转动
,绕y轴转动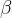 ,绕z轴转动
,绕z轴转动
根据旋转矩阵求解 三个角度;

7.2、欧拉角
欧拉角(运动轴):B坐标系绕B坐标的z轴旋转得到坐标系,然后绕坐标系
的y轴旋转得到坐标系
,最后然坐标系
的x轴旋转得到最终的坐标系 B。计算旋转矩阵需要使用2个知识点:
a、矩阵依旧采用第二章中旋转矩阵的形式,只是角度转动比较特殊。
b、5.2节知识,绕运动轴连续转动,采用从左向右的方向乘。
7.1.1、特殊情况,每次绕轴旋转90度角

7.1.2、一般情况,绕x轴转动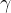 ,绕y轴转动
,绕y轴转动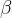 ,绕z轴转动
,绕z轴转动
RPY角和欧拉角的旋转矩阵相同;但是角度的定义和运动方式是不同的。
8、旋转变换通式:旋转向量,向量长度为旋转角度。
旋转变量通式需要证明的2个问题:

8.1、正解,已知三维的单位向量k和角度 ,求解旋转矩阵
,求解旋转矩阵
已知坐标系A,进过三维旋转得到坐标系B;三维旋转可以理解为以A坐标系为原点的某个单位向量k,将坐标系A绕向量k旋转角度得到坐标系B。
8.1.1、获取三个分量

理解要点:
a、旋转矩阵 为何第三列为
向量 以A轴原点为起始点的单位坐标,所以
,第三列代表坐标系
的z轴在坐标系A的分量,与第2章旋转矩阵的定义相符合。
b、为何 两个旋转矩阵相同
注意四个坐标系的定义;坐标系A、B开始为重合的2个坐标系,坐标系 、
开始也是重合的坐标系;
、
两个坐标系的z轴与向量k重合;A绕k向量旋转
角度得到B,同步
绕k向量旋转
角度得到
;所以
坐标系相对A坐标的位姿 等于
坐标系相对B坐标系的位姿,因此两个旋转矩阵相同。
c、旋转矩阵描述
针对 、
两个坐标系的z轴与向量k重合,绕z轴旋转
角度的旋转矩阵可以如下表示:
8.1.2、旋转动作拆分

理解要点:
将 拆分为三个旋转矩阵相乘的形式,将1次旋转变换拆分成3次旋转变换。
8.1.3、将拆分量带入计算结果

8.2、逆解,已知三维旋转矩阵 ,求解单位向量k和角度
,求解单位向量k和角度
8.2.1、问题描述

8.2.2、问题求解
























 6948
6948

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








