学习（线性、拓展 、无迹）卡尔曼滤波的完整总结

这篇文章是根据 Kalman Filter From Groun Up 这本书来总结的。这本书写的是真的太棒了！强烈推荐，虽然是英文，但完全不影响阅读。作者通过一些巧妙的叙述过程，避开了那些特别难的推导，有一些难的部分，作者也说可以跳过，真的不像中文的书籍写的无趣且晦涩，要不试读一下前50页试试感觉？没有任何废话，看似400多页，实际上花两三个小时就可以读100页，每页内容不多。整本书循序渐进，读完只觉得酣畅淋漓。我的总结只针对读完了这本书或者正在读的人写的，如果没有读这本书，下面是链接，总结只是在某些关键点做分析，会帮助你快速抓住文章重点，更好的理解。

B站有个up主：滴Bug 讲了这本书前面200页左右（视频时长七小时），可配合观看。都结合起来理解卡尔曼滤波没有任何压力。

pdf 在下面的链接

链接：https://pan.baidu.com/s/1XqFBNmAnmijv7vQRfaspzA?pwd=utuv 
提取码：utuv

关注，点赞！这个pdf是我花钱买的，让我开心开心，我才能继续分享, 我下一步准备分享几篇卡尔曼滤波估算SOC的应用实例，参考的是Gregory L. Plett博士的经典文献，最后我还会考虑用到单片机上，不知道行不行，不行的话我就阉割版

线性卡尔曼滤波

在前面的四个章节中，作者从α Filter, 再到α-β Filter，再提出α-β-γ Filter。实际上名字长度的增加只是表示系统的状态的量的增加，并且这些变量之间有一定的关系。如果没有关系，那么我想就都是叫做α Filter，比如有个系统状态变量是质量和温度，它们二者没有关系，所以每次测量的时候，都只是用一个α Filter来估计，而速度和位移作为状态变量，就需要α-β Filter。

系统只有一个变量时候，有一个例子用的是重量来作为系统变量，就叫做α Filter（作者没说是，我猜的，毕竟这样的滤波器可能实用性不强），当系统的状态是速度和位置的时候，变成了α-β Filter。当系统的状态是速度、加速度和位置三个变量的时候，就变成了α-β-γ Filter。并且有的例子中α,β,γ的值是稳定的，有的需要每次迭代后更新。

对于α-β Filter，下面是它的状态更新方程，这种滤波器的名称来自于其两个输入变量的命名，即α和β。α-β坐标系统是一种用于描述三相电流和电压之间相位关系的坐标系统。

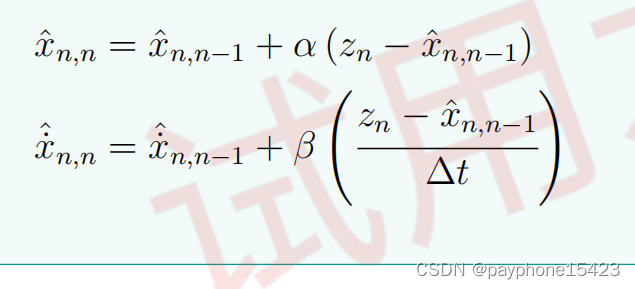
这是α-β-γ Filter（系统有三个变量）的状态更新方程

这些α，β，γ系数可能在每次迭代的时候是固定的，或者是每次迭代后都会改变，视系统而定。它实际上的代表的意思是：测量值在估计值中的权重（系统在每个时刻的状态是靠算法算出来的，因此都叫估计值），这些系数大表示测量值对估计值影响很大，这些系数小表示状态先验值（根据n-1时刻对n时刻的估计）对n时刻的估计值影响大。可见，如果测量手段精准，这些系数会比较大。

一维卡尔曼滤波算法

四五两章讲的是一维卡尔曼滤波，一维指的是系统只有一个变量，比如质量，或者速度。它也是和α-β-γ Filter类似的过程，就是“预测-更新-预测”。但是它不再只是孤零零的一个估计值（加权平均值），还把这个估计值的不确定性一起加入进去。比如，在一个系统之中，我们根据一个测量通过更新方程获得了系统当前的状态，这个状态值拿到手中，难道我们就敢百分百确定它是对的？毕竟系统状态我们是不知道的，假设换个说法：测得某个状态值是多少，它的不确定性是1，同时根据另外一套算法，虽然状态值一样，但是不确定性2，那么我们更愿意采用不确定性为1的，说明它和真实值更接近，而这个不确定性是依靠方差来度量的。

预测方程是根据当前测的状态，推断下一个时刻的状态的，预测的过程是和系统模型有关的（比如测质量的模型，以及预测速度和位置的模型，它们不一样），因此状态外推方程（预测方程）是不固定的，根据情况来定。同理，估计的不确定性的外推方程也是根据系统来的。

而，剩下的三个方程（卡尔曼增益方程，状态更新方程和协方差更新方）则形式上一样。

我下面是手写的分析，读了你就懂了。

首先是讲下81页为什么求导。非常重要

把这个卡尔曼增益带入两个更新方程

所以看接下来这幅流程图被我画圆圈的部分中，其是先根据测量不确定性rn和pn,n-1求得卡尔曼增益，再带入两个更新方程。而求卡尔曼增益的这个过程，就能保证对当前状态估计时不确定性是最小的，从而提高可信度。

第五章引入了过程噪声，过程噪声不能精确测量，它也是一个很模糊的东西，因此把它加入了协方差外推方程，就只是用一个q表示过程噪声，加在后面就好了。

一维卡尔曼滤波其它部分就没啥好说的了，书上都说的比较好。一个好的滤波器设计必须要好的模型，能够反映最真实的情况，比如一个锂电池模型，如果根据这个模型建立的卡尔曼滤波器能够很好的反映真实的电池的电量曲线，那么用它开发的估计电量的算法的时候就会比较准确。

多维卡尔曼滤波

多维指的是用一个状态向量（一个变量）来表示系统，虽然之前的一维滤波器中，有的系统状态变量三个，比如位移，速度，加速度的，但是它们的更新方程还是分开来的，就还是自己算自己的，算不得多维，现在是用一个向量来表示全部的信息。所以那5个方程就要变成矩阵形式。（一维卡尔曼滤波可以简单的看成是多维卡尔曼的特殊情况，它刚好避开了矩阵形式）。

协方差是衡量两个变量之间的相关性的，就比如A比量不断增加，B变量也增加，说明有正的相关性，如果B是减小的，就是负的相关性，如果B一直保持不变，就没有相关性。

这是计算两个变量之间的协方差公式（定义式子下面会提到）

非常重要！139页底部的例子可能不好理解，它的意思是有两个一维变量X,Y，它们分别有四次取值，我们可以带入上面的公式算出协方差。但是，如果把变量的数次取值看成一个向量，就可以在计算协方差时的累加（上面标柱）看成一个行向量和列向量相乘，简化计算。如果向量的元素就是普通的值，那么两个向量之间谈协方差没有意义。

协方差矩阵就是N维向量中每个变量与向量中的全部变量求得协方差（包括自己）后组成的矩阵。

141页的计算是两个变量，它们都有四次取值，求协方差矩阵，所以协方差矩阵是2*2的

142页顶部那个式子有问题，应该是一个向量X，它有n维，也就是n个变量，而不是n个元素。

根据定义求一个状态向量的协方差矩阵，其中X是一个向量

其中调用了两个普通变量的协方差的定义式：

一个变量的方差的定义是

所以，一个状态向量的协方差矩阵的计算办法就是：

ux是随机变量（状态向量）的平均值，它也是一个向量，它的每个元素是个值，这个值是这个位置的变量的平均值（状态向量多次测定才能得到一批数据，才能计算协方差矩阵，就测一次状态向量没必要算）。

多元随机变量的正态分布公式可以先不看。

在第八章的公式中，首先说的是状态外推方程，即从当前时刻状态估计下个时态状态，它有个通用的式子，意思自己对照书上

把握住：F是系统过渡矩阵，它不是什么协方差矩阵，协方差矩阵是为了计算估计的不确定性设计的，F是根据模型的来定义的，当然G也是由系统定义，如果系统没有输入，就不需要G，当然，过程噪声因为不能测量，就把它放到协方差外推方程中了。

附录C的意思是

任何一个线性时不变系统，都可以由如下状态空间表达式来表示（当然这应该是信号与系统里的内容），这不是卡尔曼滤波器需要的，我们需要对下面的方程方程求解得到F或者G，书上有对线性时不变的解释。

协方差外推方程

Q是过程噪声，在一维也讨论过过程噪声q,如果q过小则会使得估计值滞后，如果q太大，就会使得估计值中测量值占的权重高。我很想用一个通俗的话说，可能会有错误，过程噪声是很难量化的，我们只有不断调整它让估计的和真实的更加的接近，那么我就说我的这个系统模型以及过程噪声，很好的模拟了真实的系统。

讲一些下163页的例子的意思。对于一个恒速运动，其加速度是不变的，但是如果加速度变了，那么它就会造成速度和位移变化。163页的例子就是说，用加速度的方差来计算速度和位移的变化。但是它计算Q的方法我没有理解，欢迎留言。

测量方程

gpt的话来解释测量方程的意义

在卡尔曼滤波中，观测方程的主要目的是将系统的状态映射到测量空间，从而建立观测值与系统状态之间的关系，观测方程描述了如何从系统的状态空间中生成观测值。因为，测量值不一定测得就是系统状态，有可能就是反映系统状态得其它量。结合下面这个多维状态更新方程理解。比如，系统状态向量有5个变量，测量只能测3个，那么Zn就是一个三维向量，它不能和一个五维的状态估计向量作算术减法，必须用H把状态估计变成测量值，相减完后，通过卡尔曼增益K又变成5维的状态向量X。观测方程在这个过程中起到了连接系统状态和观测值的桥梁的作用。

已经说了三个方程了，两个外推，一个测量方程，上面也说下了状态更新方程

状态更新方程

卡尔曼增益后面会说，关注下维度，维度只是为了保证计算能顺利进行

协方差更新方程

卡尔曼增益方程

它的推导过程和一维卡尔曼增益思想一模一样，希望Pn,n是最小的，即系统估计的方差最小，这样系统估计的值精确性就高。是先算卡尔曼增益，再带回更新方程，计算卡尔曼增益的过程就确保了下个时候的估计可信度是最高的。

简化的协方差更新方程

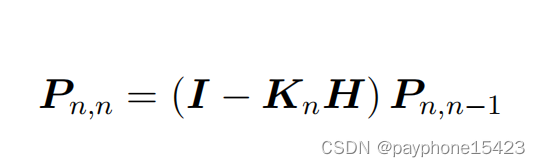
后面举了两个例子，它是先算出各变量大概的式子，然后再初步设定一些值，不是初始化，这更像是一种试错，只有好的参数设定，才能更加准确。

多维线性卡尔曼滤波说完了。

拓展卡尔曼滤波

之前都是讨论线性系统，现在是非线性系统，书中有提到线性时不变系统，可自己看一下。非线性系统有什么特征呢？书上说了两种特征（227页）

1是状态到-预测的非线性，也就是观测方程是非线性的

2是系统动态模型是非线性的，系统的动态模型在之前的线性系统中做的如下的定义：

可见：如果把F这个矩阵看成一个常数，它就是一个线性系统，如果Xn+1,n 和Xn,n 之间不满足线性关系，就是非线性系统。

一个非线性系统可以同时是情况1和情况2 ，也可以满足一个。

例子12.1是线性系统；例子12.2是动态模型是线性的，观测方程是非线性的；例子12.3是动态模型是非线性的，而观测方程分两种情况，根据测量值的不同，可以为线性或者非线性的，但是由于动态模型已经非线性了，那么它就是非线性的系统。

那非线性系统会造成什么缺点呢？

请看图12.4和12.3. 在卡尔曼滤波中，的每个变量都需要服从高斯分布，那么在图12.2中，某个变量的不确定性可通过这个线性系统映射到另外一个变量中去，而在12.4中，当变量之间不是线性关系，不确定性的线性映射就会丢掉。因此非线性系统最大的影响在于状态的不确定性不能向下一次迭代传递，导致卡尔曼增益，协方差的更新这些出现问题。当然这样理解应该可以的，我是为了使用它，不是为了彻底的推导它。

所以就要克服这种非线性问题，就用泰勒展开到的一阶导来替代这个非线性的关系（泰勒展开搜一下，很简单的），使观测方程或者动态方程成为了一个线性关系，使得不确定性能够线性映射，所以拓展卡尔曼滤波是为了让不确定性能够映射成为高斯分布，而不是让状态的外推和更新也通过线性替代。可以看到在251页

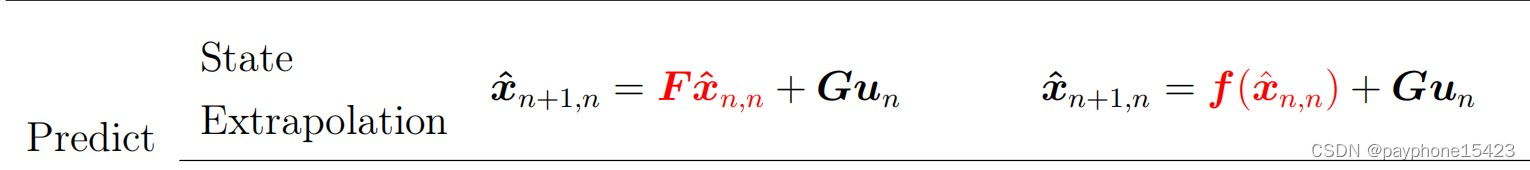
系统的动态模型和更新方程只是被替换成了函数一下，就算你是非线性又如何，你不影响我状态的更新和预测，你只是影响我状态的不确定性这个参数不能以一个高斯分布继续更新或者外推下去。

图13.1就是一个线性替代的意思

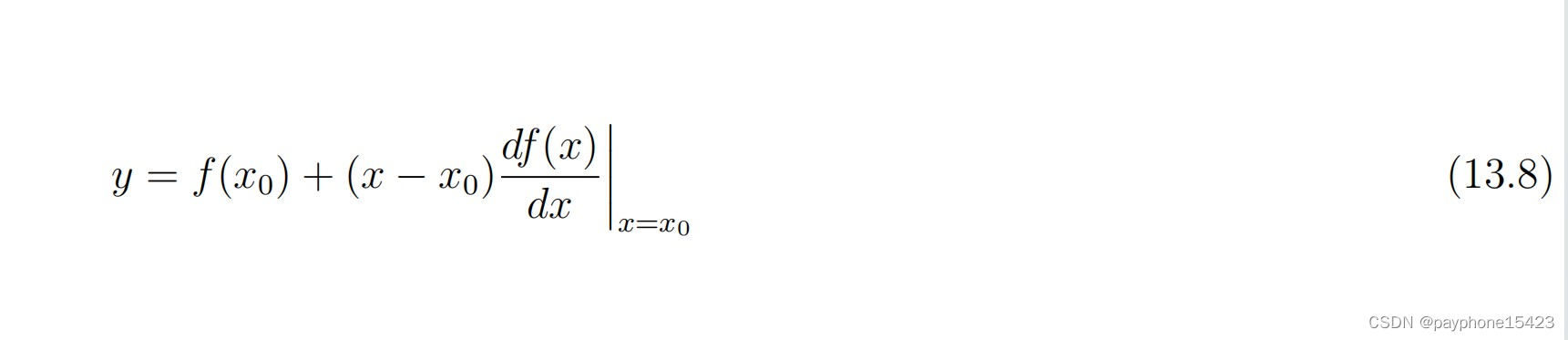
这是对f(x)在某个点的泰勒展开并舍弃高次项。图13.2说的是在一维的情况下，经过线性化，那么就可以让不确定性能够经过映射也是高斯分布。

对于多维的

如果某个方程是非线性的，那么我们对它线性化解析（就上面这个最近的方程），这个线性解析化函数我不知道怎么来的，但是我不想去了解它怎么来（它在246页说可以去读参考文献7），我可以知道它怎么用：

如果观测方程和系统动态方程是非线性的，我们可以使用如下方法去解析化，使得不确定性（多元里叫协方差了）能够线性化。我们在上面已经讨论了，拓展卡尔曼滤波是为了让系统不确定性一直能高斯分布下去，所以下面的这两各解析化函数的意思就是，如果观测方程和动态方程是非线性的，我们只需要计算观测方程函数它对变量中每个元素的偏导并组成一个矩阵（这个矩阵就是雅可比矩阵），然后自变量的不确定性（协方差）可以通过这个方程实现线性化，Pin就是输入协方差，Pout就是输出协方差，那么不确定性就实现了近似替代。从而解决了非线性系统的不确定性不能持续高斯分布的问题

我画圈的部分，就是上面提到的问题，就算非线性系统，也不影响状态外推和状态更新，和状态相关的都没变，因为它们本来就满足这样的关系，再线性替代就更不准了！第二行，用这个雅可比方程替换F过渡矩阵我觉得很自然，毕竟都是线性系统了，但是下面协方差更新和卡尔曼增益方程的的替代我有点没有懂为什么，但是只觉得看似很合理，如果推起来我觉得应该是把线性卡尔曼滤波的协方差更新方程和卡尔曼增益展开，然后会得到类似线性协方差外推方程这样的式子，但是此时不是和f(x)有关，但是和h(x)有关，就需要把h(x)对x的偏导带入替换，也就是上面提到的解析线性化的式子，然后又不断的化简，就得到了拓展卡尔曼滤波的协方差更新方程和卡尔曼增益方程。我不想推了，也没必要去推理，就知道这些我觉得也足够了。我们用线性替代实现了非线性系统的的处理，那么就实现了拓展卡尔曼滤波。

无迹卡尔曼滤波

【自动驾驶】学习卡尔曼滤波（三）——无迹卡尔曼滤波_无迹变换-CSDN博客

可以结合这个看看，这篇文章讲了为什么引入无迹卡尔曼滤波：讨论拓展卡尔曼滤波的时候，说了非线性系统会使得系统的状态的不确定性不能维持高斯分布，即概率密度函数不是对称的，我们使用线性化手段（泰勒展开）来模拟这个非线性系统，但是其必须要计算雅可比矩阵，会使得计算量大。无迹卡尔曼滤波的思想是：就算一个高斯分布的变量经过非线性系统的后的概率密度函数是奇怪（不能维持高斯分布）的，但是通过无迹变换把这个变量以及它的不确定性在经过非线性系统后显示出一个近似正态分布的样子，替代那个真实的并且奇怪的概率密度函数。

即：近似非线性函数的概率分布要比近似非线性函数本身要容易

我们之前说了，非线性系统是有有可能是在测量方程或者系统动态方程出现，那无迹变换（从284页到297页都是无迹变换的内容）只是实现一个变量以及它的不确定性（多元叫协方差）经过一个非线性系统后，得到了一个近似正态分布的变量和不确定性，它只是UFL中的一个非常小的步骤。回想一下之前拓展卡尔曼滤波，如果你是非线性系统，那我把你这个非线性函数线性化，那么变量经过这个系统的后不确定性就能保持高斯分布。而无迹卡尔曼滤波则是，不去对这个非线性化函数线性化，而是用一个变换，同样也实现了一个高斯分布的随机变量在经过非线性系统后也维持高斯分布。（刚刚已经说了，又重复啰嗦了一下）。

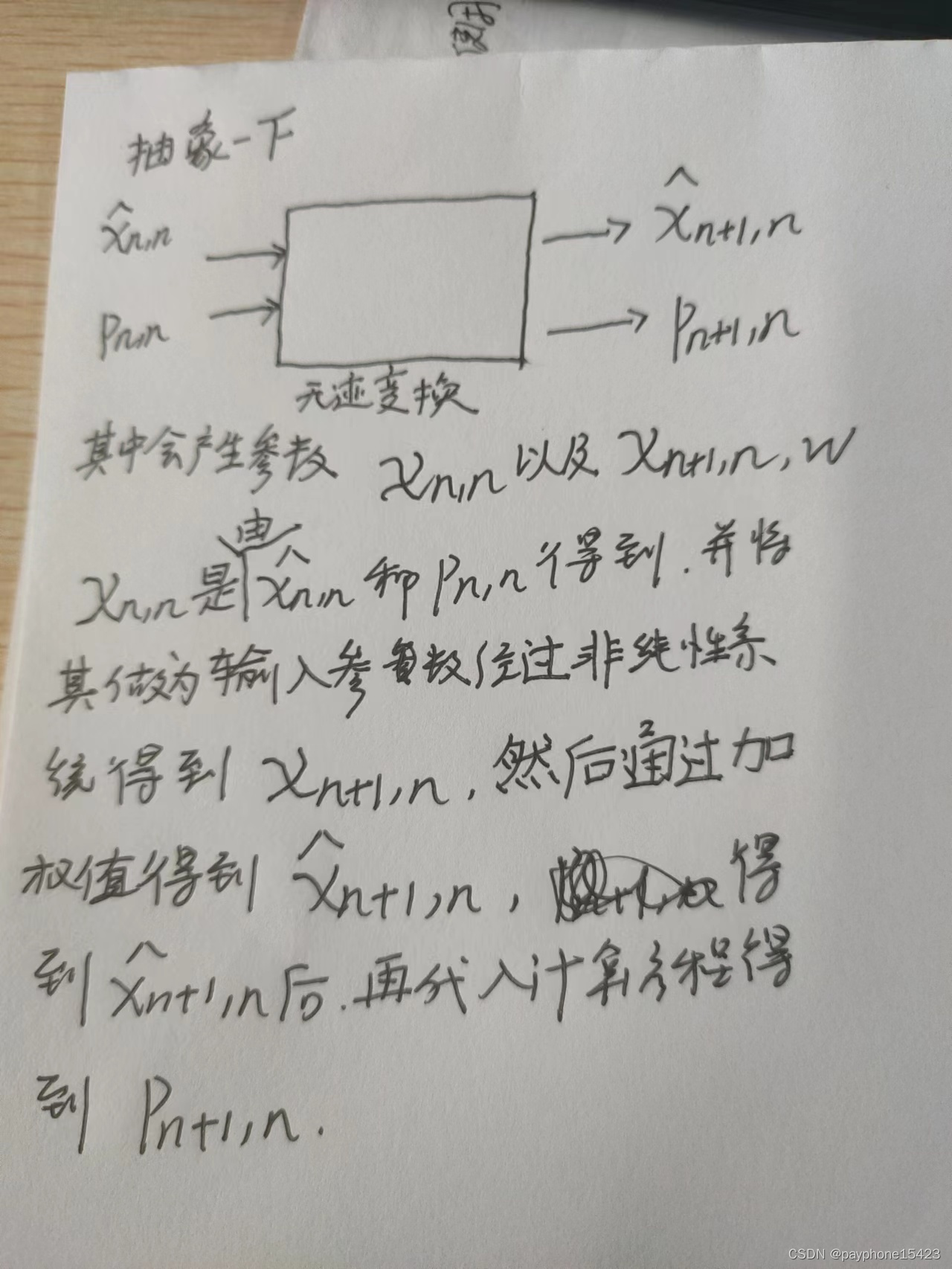
讲一下这两个图

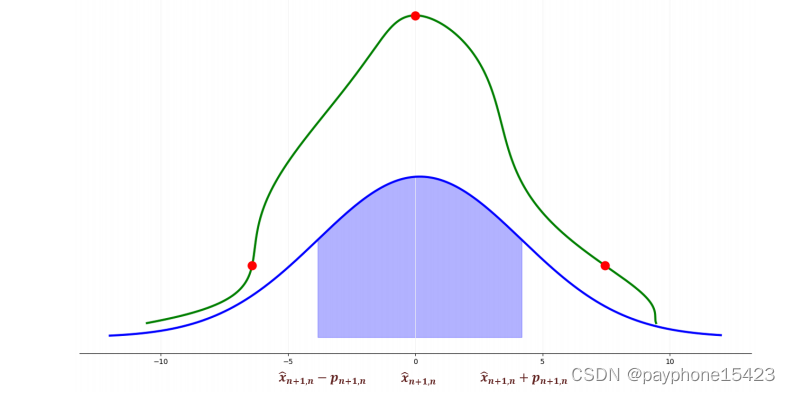
绿线只是经过了非线性系统的输出的概率密度函数，其还没有加权求Xn+1,n

而蓝色的经过加权求和的

可见，经过一番操作，符合正态分布了。在二维情况也是，输入变量的概率密度函数的是一个正态分布的椭圆，经过非线性系统后得到的中间值的概率密度是弯弯的，而经过加权后，又是一个椭圆了。

正式开始进入无迹卡尔曼滤波

从预测开始，也就是状态外推方程，使用的就是无迹变换，实现了以下这个形式

14.3 节的统计线性回归有必要讲一下，它的意思是用一条直线来反映这些些取值的趋势。比如y=x^2,取值1，2；2，4；3，9 。它们肯定不在一条直线上，但是我希望一条直线能够反映它们的趋势，就要做回归分析，让某条直线尽可能代表它们。比如我做实验，配某个物质的标准曲线，5mg/L的紫外吸光度是10，10mg/L的吸光度是19，15mg/L的吸光度是31，我希望它完全按照10，20，30，但是它确没有。仔细一想发现它们的线性关系其实已经很明显了，虽然它们三个点不在一条直线上。我经过一通操作，生成了一条直线反映了它们的关系。

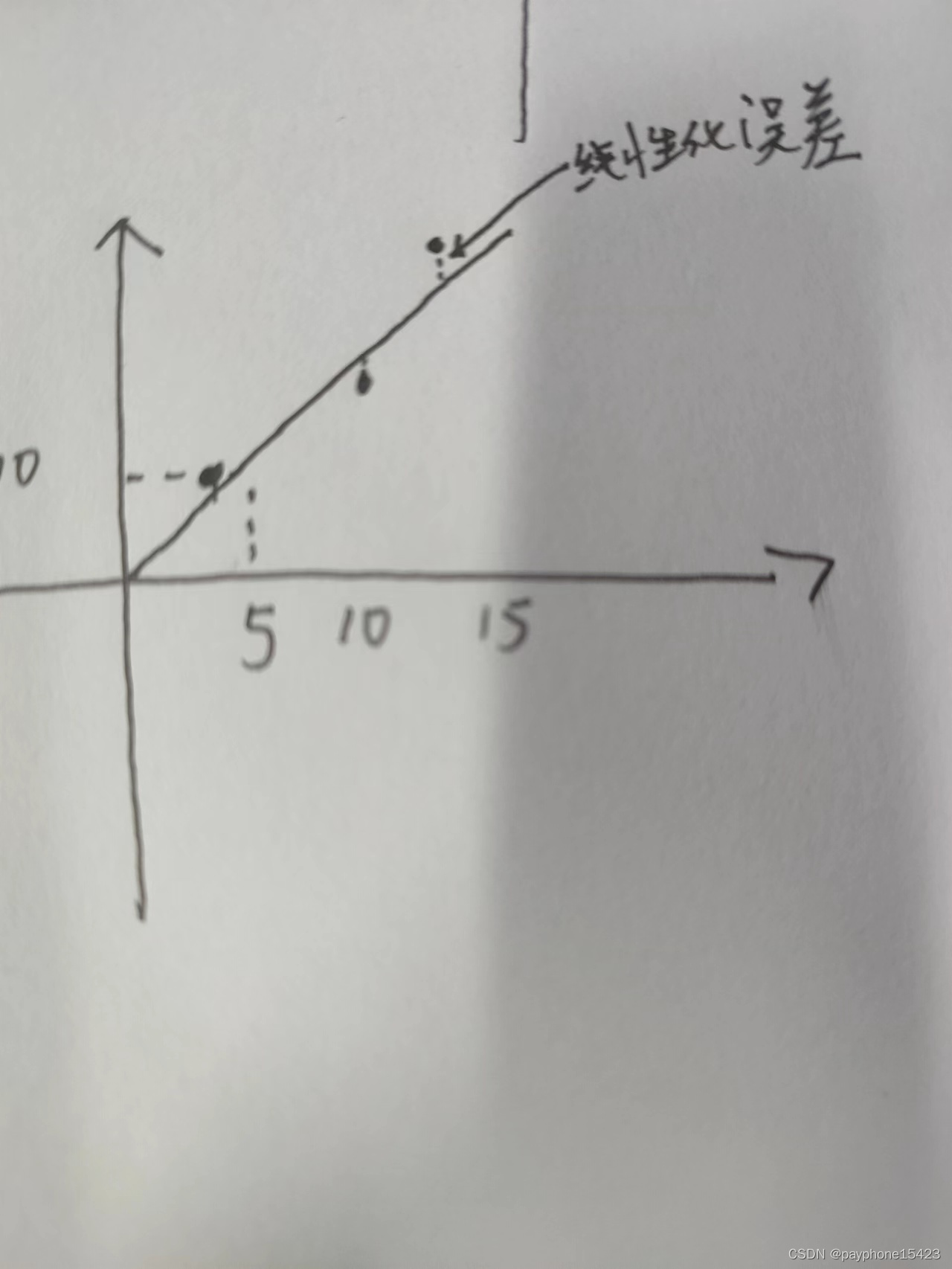
线性化误差计算如下，如图中标柱

为了使得线性化误差最小，那么就要寻找最合适的M和b。（方程14.13的b的计算方法有错误，是y的均值，不是z的均值）

解释下这里

其中

那么

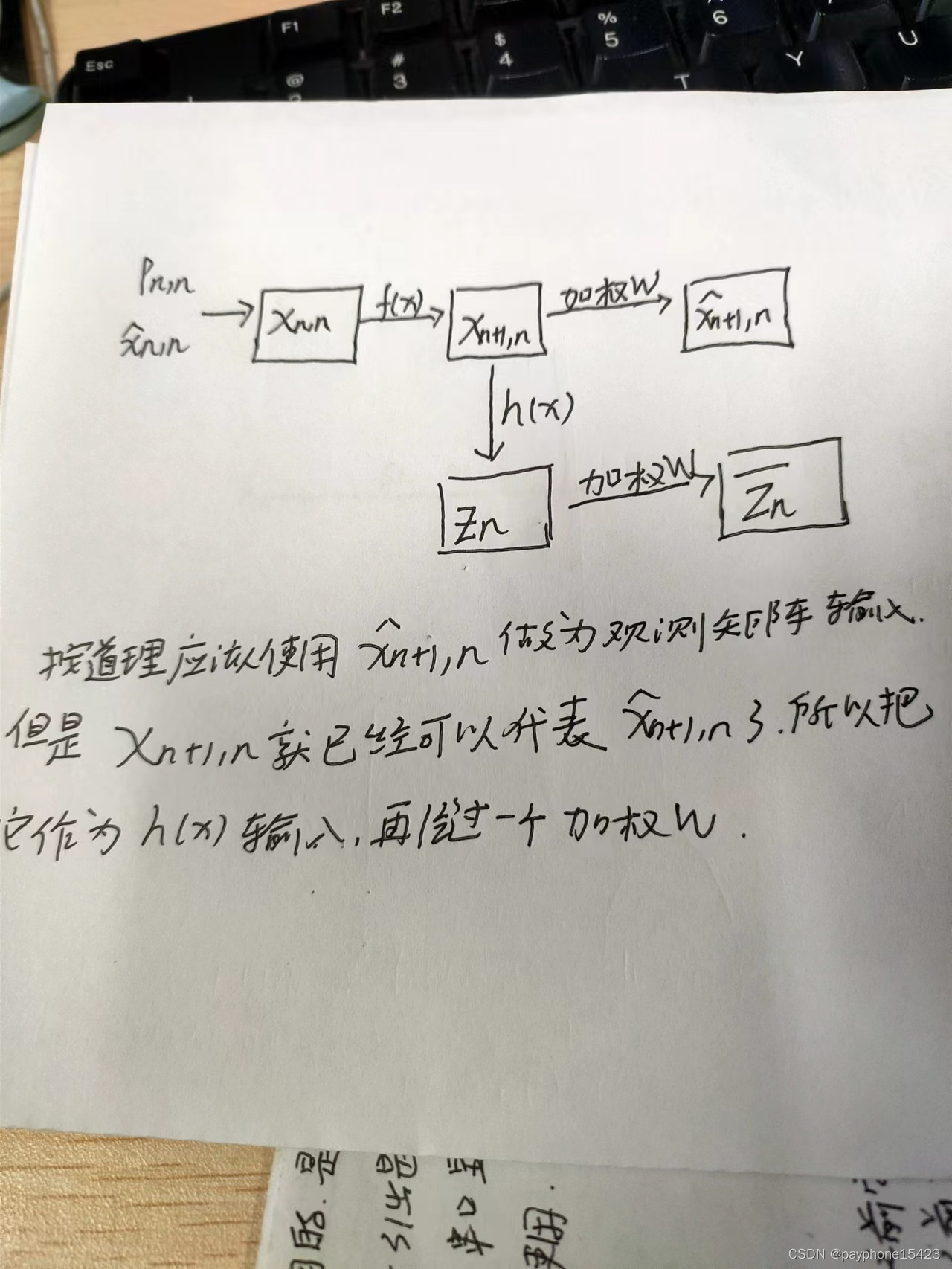
测量方程中的输入参数就是我们在状态外推方程（无迹变换）中得到的一个中间参数，这里理解一下，不要搞混了。

大概是这样的关系

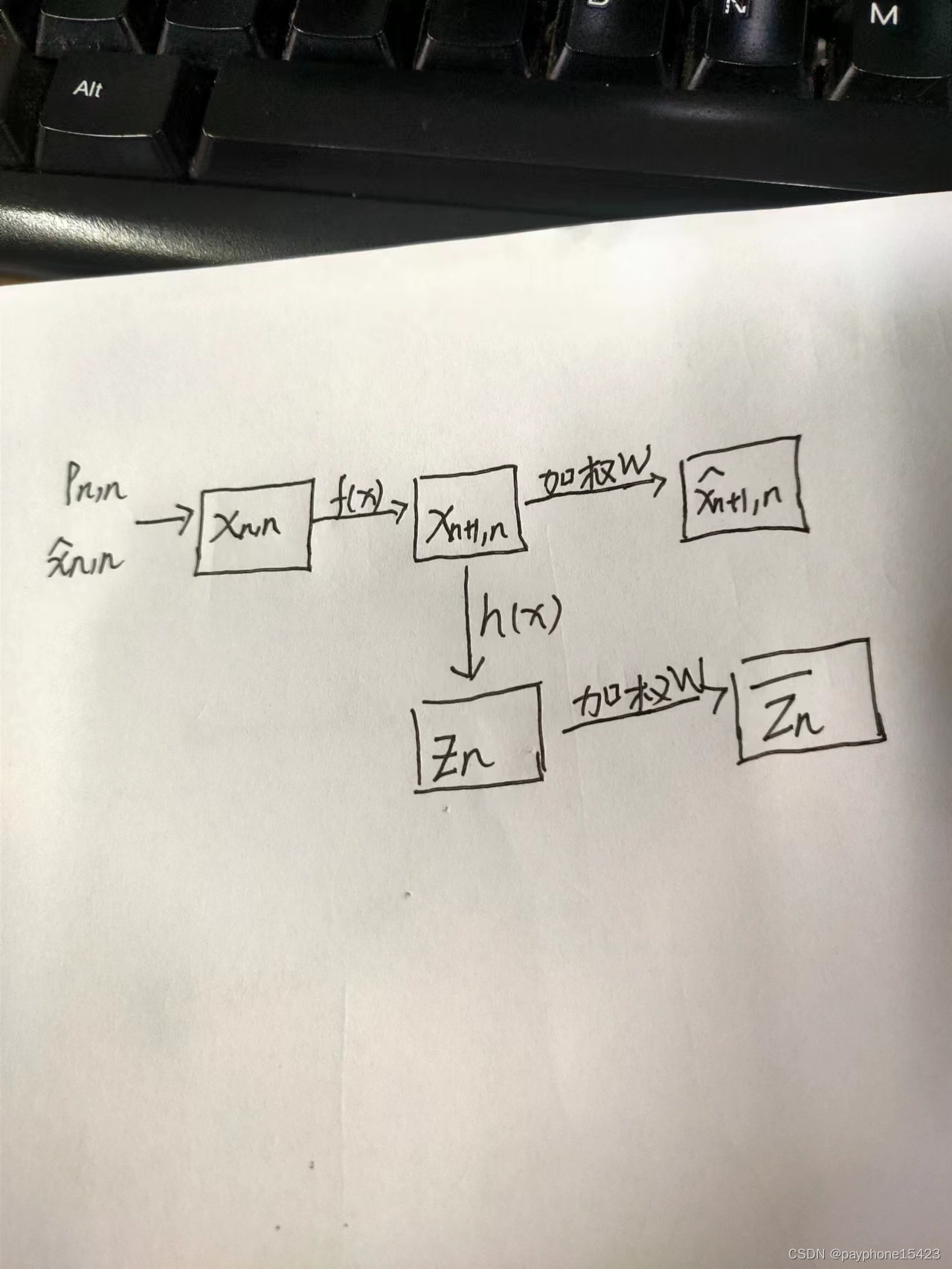
为什么这样做？之前说了测量方程是沟通系统状态和测量值之间的桥梁。这是线性卡尔曼的状态更新方程

可以看到，观测矩阵就是为了实现把当前状态的先验估计变成一个测量值然后和当前的观测值做减法，不然测量值怎么能和系统状态值做减法呢。而卡尔曼增援的作用则是把测量值（比如三维的）变成一个系统状态值（5维的），并且反映测量值在当前状态估计值中的占比。

回想线性卡尔曼增益的推导原理：它希望对当前状态估计的不确定性是最小的，对不确定性的外推方程求导，令导数等于0，求得卡尔曼增益再返回带入不确定性外推方程，这样使得当前估计的不确定性小，上面有提。

此处也是相同的思想，只不过采取了一个所谓的回归线性化思想

其中innovation大概的意思是 = 实际传感器测量值 - 传感器预测值，传感器预测值就是上面观测方程的输出值，其是一个均值，（卡尔曼滤波中的状态值，预测值都是均值）。也称为测量残差

翻译下这句话：卡尔曼增益是把测量残差和测量误差通过线性回归变换从测量空间转移到系统状态空间。

在线性回归的过程中，根据一些算法，产生了一条直线，使得X轴的观测变量经过这个直线，变换成了状态变量，而在生成这个直线的过程中确保了线性化误差是最小的。

然后推得K=M，其实这里我也不是很懂为什么K=M，就反正求得了卡尔曼增益。

希望懂得人说一下。

求得卡尔曼后，直接带入更新方程

在它得总结图中，说一下这个

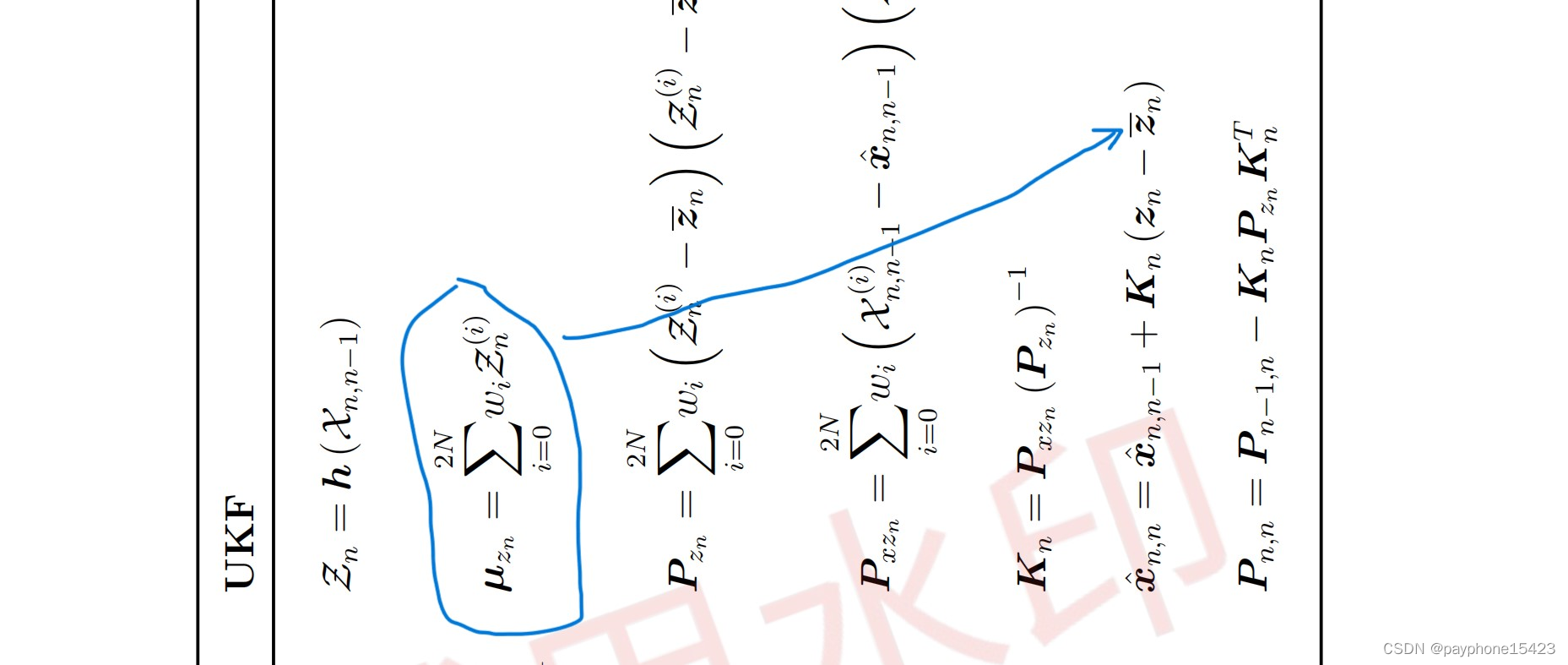
后面说了新的方法来计算无迹变换中的权重，没什么好说的。

至此，线性，拓展，无迹卡尔曼滤波就完了。后面我觉得都很简单

点赞关注啊，我学了半个月。