系统建模与仿真之利用相关分析法辨识脉冲响应

        在这里分享我们《系统建模与仿真》课程的实验课的matlab编程题目，虽然我写的可能不太好，但是代码也可以给初学者提供参考。

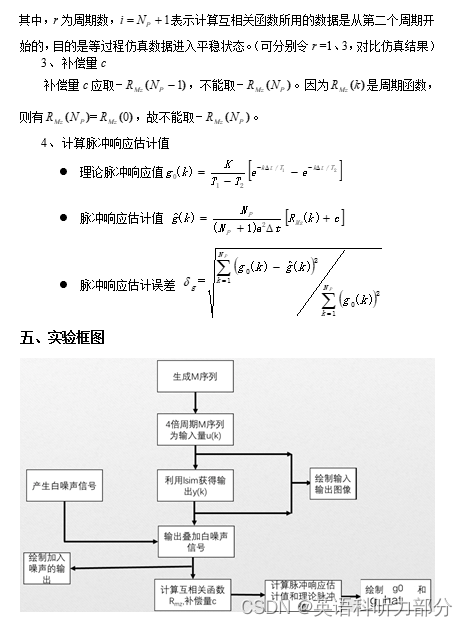
        本实验以4倍M序列作为辨识信号的例子，通过仿真实验掌握利用相关分析法辨识脉冲响应的原理和方法。

实验报告部分

 

        

                        

代码部分

链接里是别人写的参考代码，但是分成了多个函数，看着不方便，而且有些可以修改。

这里因为我做这个实验，所以自己写了代码，供同校以及其他有需要的人参考。

程序如下：

clear;%清屏
close all;
clc;
%生成m序列
r = 3;
a = 1;
delta_t = 1;
M = [1, 1, 0, 0, 0, 1];%设置6位寄存器
Np = 2^length(M)-1;%M序列周期
u = zeros(1,(r+1)*Np);
for i = 1 : (r+1)*Np
    u(i) = M(6);
    m = xor(M(6),M(5));
    M(2:6) = M(1:5);
    M(1) = m;
end
u = (1-2*u)*a;
figure,hold on
plot(u);
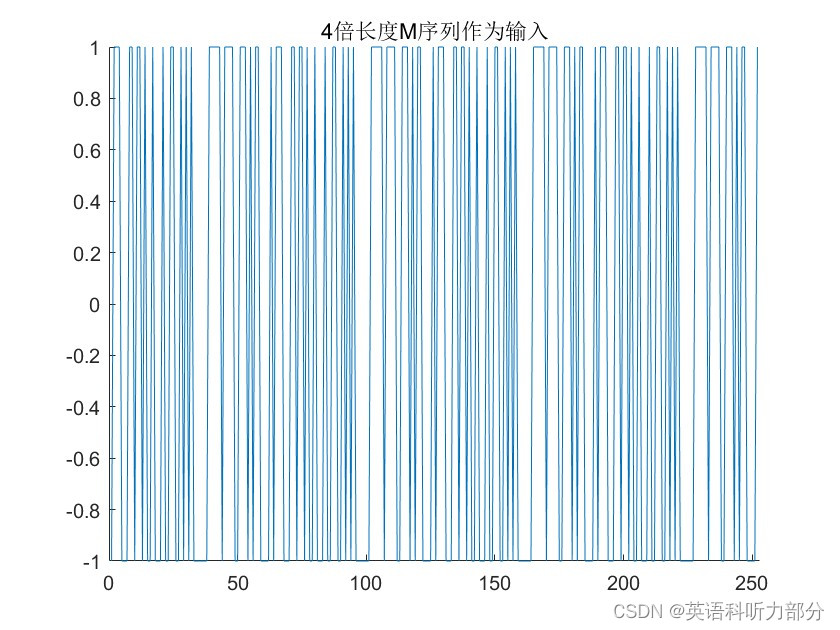
title("4倍长度M序列作为输入");
xlim([0, (r+1)*Np+1]);
hold off
%白噪声
A=27;x0=41;M=2^16;Num=(r+1)*Np;N=Num*30;
v=zeros(1,N);
for k = 1:N
    x2 = A*x0;
    x1 = mod(x2,M);
    v1 = x1/M;
    v(k) = v1;
    x0 = x1;
    v0 = v1;
end
B=reshape(v,Num,30);
noise=zeros(1,Num);
for i=1:Num
    noise(i)=(sum(B(i,:))-30/2)/(sqrt(30/12));
end
figure,hold on
histogram(noise,12); 
hold off;
% estimate g
T1=8.3;T2=6.2;
den = [T1*T2, T1+T2, 1];
K = 120;
G = tf(K, den);  
tt=0:length(u)-1;
Y = lsim(G, u, tt);
Y=Y';
Y_noise = Y + noise;
figure, hold on;
plot(1:length(noise),noise,'g');
plot(1:length(Y), Y,'r');
plot(1:length(Y_noise), Y_noise,'b');
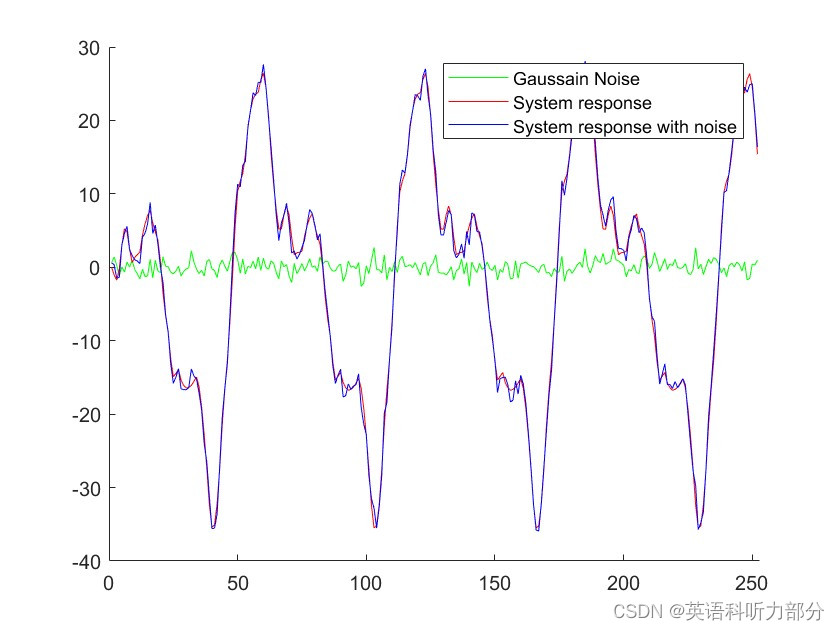
legend(['Gaussain Noise',"System response","System response with noise"]);
xlim([0, length(Y)+1]);
hold off
time = 0:delta_t:(Np-1)*delta_t;
g0 = (120 / (T1-T2)) * (exp(-time./T1)-exp(-time./T2));%理论
Rmz=zeros(1,Np);
for tch=1:Np
    SUM=0;
    for tcl=Np+1:(r+1)*Np
        SUM=SUM+u(tcl-tch)*Y_noise(tcl);
    end
    Rmz(tch)=SUM/(r*Np);
end
g_hat=Np*(Rmz-Rmz(Np-1))/((a^2)*(Np+1)*delta_t);%估计
g2=g0-g_hat;%误差
figure, hold on
plot(1:Np, g0, 'r');
plot(1:Np, g_hat, 'b');
plot(1:Np, g2);
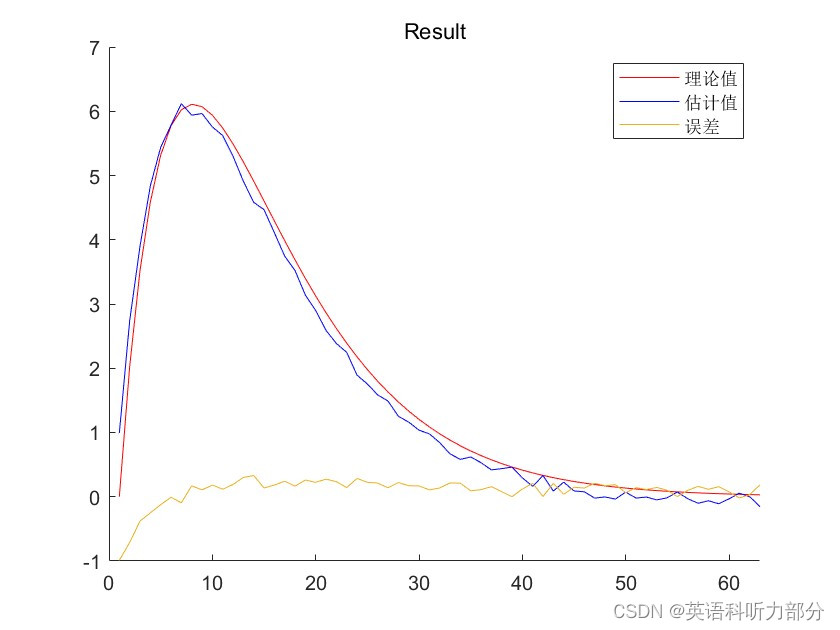
title("Result");
legend(["理论值","估计值","误差"]);
xlim([0, Np]);
hold off
figure,hold on
title("Rmz");
plot(1:Np, Rmz, 'r');
xlim([0, Np]);
hold off;
error_sum=0;square_sum=0;
for count=1:Np
    error_sum=error_sum+(g0(count)-g_hat(count))^2;
    square_sum=square_sum+g0(count)^2;
end
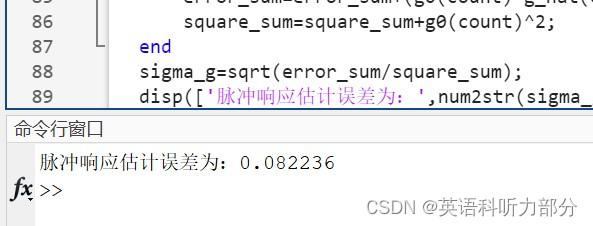
sigma_g=sqrt(error_sum/square_sum);
disp(['脉冲响应估计误差为：',num2str(sigma_g)]);

 

运行图片

 

实验结论

        实验生成了M序列以及满足标准正态分布的白噪声，并将M序列作为输入使用相关分析法辨识系统的脉冲响应，利用维纳霍夫方程辨识得到脉冲响应的估计值，同时直接通过公式算术得到并且用MATLAB画出脉冲响应的理论值，将两者对比，计算得到脉冲估计误差为0.082236。可以看到脉冲响应的理论值和估计值的图像比较接近，辨识效果较好。本次实验达到预期目标。

注意和问

        有人可能会问：误差0.082236不是挺大的了，平均8%了，其实是因为我懒而且没弄透原理，可能估计值图像右移一曲线能够更加贴合，但是这就会有什么矩阵行列不匹配类似的事就有些无休止了。如果你们交作业把误差作为评分标准的话，你们自己修改下例如在前面加一项0或者别的什么方法使其匹配。（这不是投机取巧，Y如果不加Noise进行辨识会发现图像是完美右移的状态，我也不好说） 我也不太懂，还是说不用改代码，有知道的人可以回复下。

修改参数比较

修改重复次数

修改为2倍M序列，即r=1，识别图像如下。

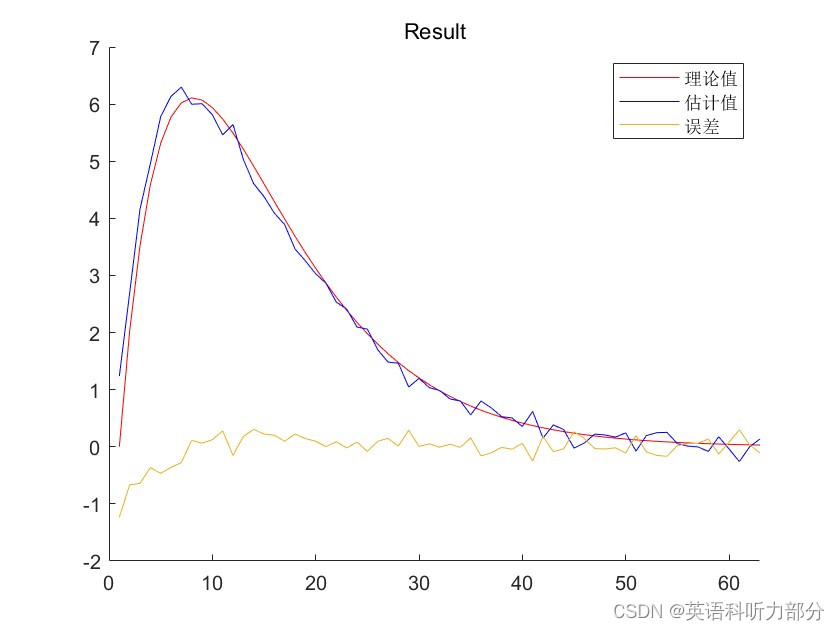
标题2倍M序列

我们可以发现识别效果比4倍M序列效果差。