什么是安斯库姆四重奏？为什么统计分析之前必须要作图？

欢迎关注"R语言和统计"~~

Anscombe's quartet，Wikipedia

就现在的习惯来说，统计表格和作图往往是同时出现的。

比如，在使用表格呈现相关或回归系数等统计值的时候，通常还会配上一个散点图用来辅助说明。

现在很少有只做表格，不画图的“老一辈风格”啦。

不过，大约1973年的时候，大部分的统计学家们却持这样的观点：用统计值来描述数据才是准确的（比如均数，标准差，相关系数等），而图片是粗略、不准确的[1]！

就在这时候，有一位名叫Francis Anscombe的统计学家，写了一篇论文“ Graphs in Statistical Analysis”，发在了《The American Statistician》杂志上，想要凭借一己之力逆转当时的“不良风气”[1]！

他创建了4组数据，如下： 

上述四对数据（两个变量：x，y）拥有相同的统计描述： 

x的均数为：9，方差为：11

y的均数为：7.5，方差为：4.13

x和y的相关系数为：0.82

随后，作者作了一个散点图，并且画出了回归直线，见下图： 

Anscombe's quartet，Wikipedia

结果令人震惊！

如果只看均数，方差等统计描述，会误认为数据是一样的！更糟糕的是，再强行使用线性模型，拟合出的方程将会变得非常不可靠！

而通过制作散点图，可以观察到数据的分布情况，如是否线性（线性回归的重要前提之一），是否存在影响点（Inflential observations）等重要信息。

只有了解这些重要信息之后，我们才可以选择合适的统计模型用于后续分析。

现在使用R来进一步了解作图的重要性，并且还很好玩！

首先，安装一个包{datasauRus}并且载入： 

# install.packages("datasauRus")
# install.packages("ggplot2")
library(datasauRus)
library(ggplot2)

作图： 

ggplot(subset(datasaurus_dozen, dataset != "x_shape"),
       aes(x = x, y = y, colour = dataset))+
  geom_point()+
  facet_wrap(~ dataset, ncol = 4) + 
  theme_void() +
  theme(legend.position = "none")

如之前所述，图片的形状差异非常巨大，但x和y却具有相同的统计描述，如下图： 

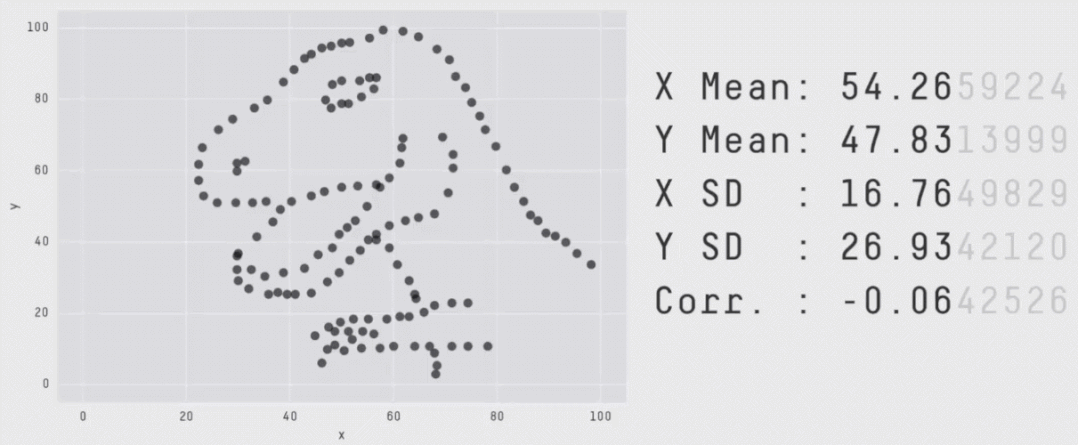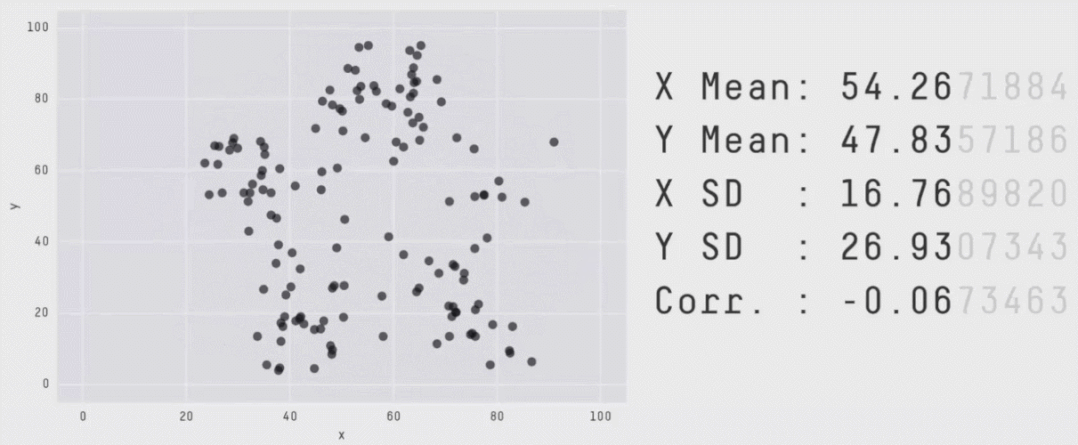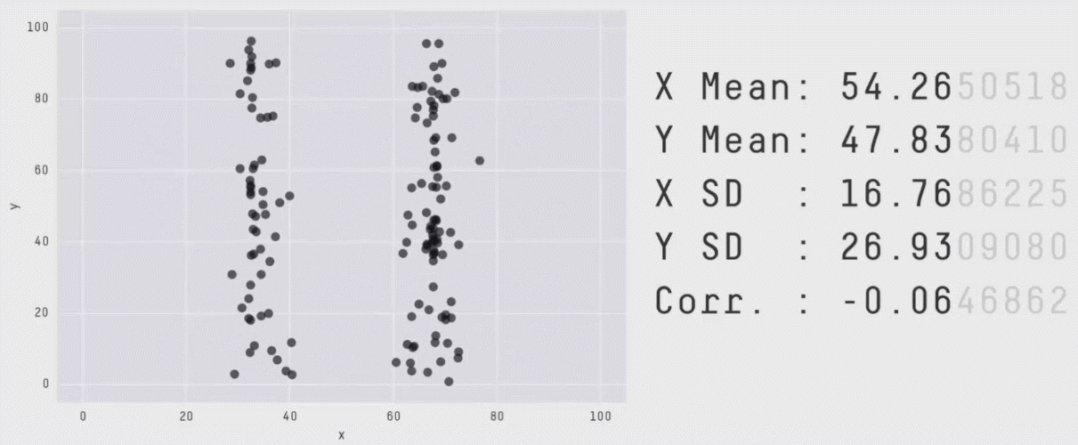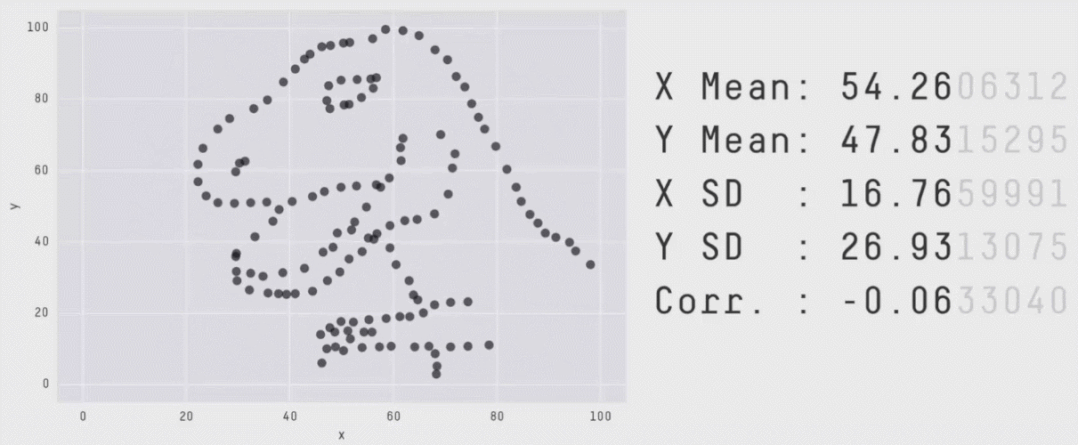
图片来源：[2]

应了那句话：有图有真相！

好啦，今天的内容就到这里。

如果有帮助，记得分享给需要的人！

参考文献

[1]. Anscombe, F.J. (1973). Graphs in Statistical Analysis. The American Statistician 27, 1, 17–21.

[2]. https://github.com/lockedata/datasauRus

▌声明：本文由R语言和统计首发，如需转载请联系我们

▌编辑：June

▌我们的宗旨是：让R语言和统计变得简单！

往期精品(点击图片直达文字对应教程)

机器学习

后台回复“生信宝典福利第一波”或点击阅读原文获取教程合集