这篇被引用近4k次的论文教你如何正确的理解和使用相关系数！

欢迎关注"R语言和统计"~~

小编前几天阅读了一篇论文，名为“A guide to appropriate use of correlation coefficient in medical research” [1]，写的简单易懂，并且在医学研究的实践中非常有参考价值，因此决定分享给大家。

虽然相关(Correlation)容易计算和解释，但是它的误用在研究者中也非常的普遍，有些统计学家甚至认为：相关的概念一开始就没有被提出可能会更好 [2] ！

所以，在最开始，先了解一下到底什么是相关。

相关的定义

在统计学中，相关是一种用于评估两个连续变量之间的线性关系的方法 [2]。

而相关系数(Correlation coefficient)可用于评估两个连续变量之间的线性关系的强度，它可以取值 -1 到 +1 之间。

假如相关系数为0，表示两个连续变量之间不存在线性关系；相关系数为 -1或者 +1，表示两者存在完美的线性关系。两者的线性关系越强，数值将会越往 -1 或 + 1 汇聚。

如果相关系数为负数，称为负相关，即当一个变量的数值增加时，另外一个变量的数值将会倾向于下降。而相关系数为正数，称为正相关，即当一个变量的数值增加时，另外一个变量的数值也会倾向于增加。

值得注意的是，如果两个变量之间的关系是非线性，根据统计学的定义，我们不能称它们是相关！

举个例子，假设在线性代数中两个变量之间的关系是：y = 0.5*x^3，可以在R中将其作图： 

# 创建数据
x <- -10:10
y <- 0.5*x^3

# 作图
plot(x, y, type = "l")
title(main = "y = 0.5*x^3")

如上图：在数学上，x和y当然存在某种联系(y = 0.5*x^3)；但是在统计学中，将x和y称为相关就不是非常的恰当，因为统计的相关指的是线性关系！

相关系数的类型

主要有两种相关系数：Pearson相关系数和Spearman相关系数[如果觉得不够，可以查看往期文章：涨知识！15种相关分析算法，总有一款适合你！]。 

到底该如何选择相应的方法？ 

这取决于所要研究的变量，如果两个变量都是正态分布，选择Pearson相关；如果其中一个或两个不是正态分布，选择Spearman相关。 

Pearson相关系数的公式如下：

Spearman相关系数的公式如下：

注：di 指的是x和y间排序的差别。

相关系数和散点图

论文作者首先创建了两组符合正态分布的数据，使用Pearson相关（相关系数分别为0.2, 0.5, 0.8, -0.8），并且制作了对应的散点图，如下： 

Pearson相关系数为 0.2时： 

图片来源：[1]的Figure 1

Pearson相关系数为 0.5时： 

图片来源：[1]的Figure 2

Pearson相关系数为 0.8时： 

图片来源：[1]的Figure 3

Pearson相关系数为 -0.8时： 

图片来源：[1]的Figure 4

上述四张图片可以帮助我们了解不同相关系数所对应散点图的样子，有助于在未来仅根据散点图的模样提前大致推测它们的相关系数。

从上述四张图片可知，相关系数越大（绝对值），两个变量之间的线性关系越明显。

实例解析

下面用一个实例，用于解释两种相关系数在实际应用上的差别。

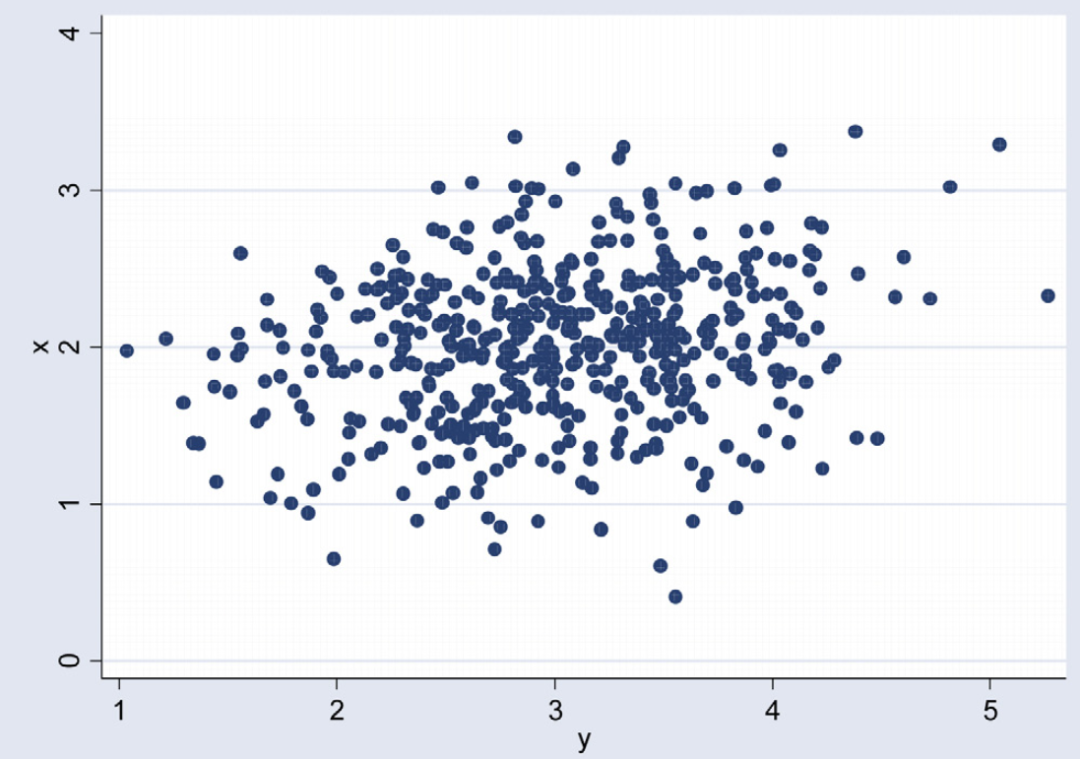
作者使用了产前门诊的数据，共包含了 750 例孕妇，选取了其中两个变量：血液中血红蛋白浓度(呈正态分布)和产次(呈偏态分布)，散点图如下： 

图片来源：[1]的Figure 5

因为产次(parity)为偏态分布，所以在这个例子中，选择Spearman相关会更加合适，计算所得相关系数为 0.3。 

如果使用Pearson相关，它的相关系数为 0.2。

根据下表，它们的相关系数将会得出截然不同的结论： 

表格来源：[1]的Table 1

如上表所示，如果根据Spearman相关系数为 0.3，可以认为变量间的相关为弱正相关。而如果根据Pearson相关系数为 0.2，它们间的相关是可以忽略的！所以，不同的方法可能会造成完全不同的结论。

好啦，今天的内容就到这里。

如果有帮助，记得分享给需要的人！

参考文献

[1]. M.M Mukaka, A guide to appropriate use of Correlation coefficient in medical research, Malawi Medical Journal; 24(3): 69-71 September 2012

[2]. Altman DG. Practical Statistics for Medical Research. Chapman & Hall/CRC

▌本文由R语言和统计首发，如需转载请联系我们

▌编辑：June

▌我们的梦想是让R语言和统计变得简单！

往期精品(点击图片直达文字对应教程)

机器学习

后台回复“生信宝典福利第一波”或点击阅读原文获取教程合集