一个神经元顶5到8层神经网络，深度学习的计算复杂度被生物碾压了

编者荐语

 

来自耶路撒冷希伯来大学的研究者对单个神经元的计算复杂度进行了研究，他们通过训练人工深度神经网络来模拟生物神经元的计算，得出深度神经网络需要 5 至 8 层互连神经元才能表征（或达到）单个生物神经元的复杂度。

转载自丨机器之心

人类糊状的大脑似乎与计算机处理器中的固态硅芯片相去甚远，但科学家将二者进行比较已经有很多年的历史。正如「人工智能之父」阿兰 · 图灵在 1952 年所说，「我们对大脑具有冷粥粘稠度这一事实不感兴趣。」换句话说，介质不重要，重要的是计算能力。

当前，最强大的 AI 系统采用机器学习的一个分支——深度学习，这些 AI 系统的算法通过处理互连节点隐藏层的大量数据来学习，这被称为深度神经网络。顾名思义，深度神经网络受到了人类大脑中真实神经网络的启发，它们的节点模拟真实神经元。或者至少根据 1950 年代神经科学家对神经元的了解，当时一个被称作「感知器」的有影响力的神经元模型已经诞生了。

自那时起，我们对单个神经元的计算复杂度的理解急剧增加，也清楚了生物神经元要比人工神经元更加复杂。但复杂多少呢？这个问题一直没有明确的解答。

为了找出答案，耶路撒冷希伯来大学的计算神经科学博士生 David Beniaguev、神经科学教授 Idan Segev 和副教授 Michael London 训练了一个人工深度神经网络来模拟生物神经元的计算。他们表示，一个深度神经网络需要 5 至 8 层互连神经元才能表征（或达到）单个生物神经元的复杂度。

作者们也没有预料到会呈现出这种复杂度。一作 Beniaguev 表示：「我原以为生物神经元会更简单些，3 至 4 层人工神经元就足以捕获细胞内执行的计算。」 

从左至右依次为耶路撒冷希伯来大学博士生 David Beniaguev、神经科学教授 Idan Segev 和副教授 Michael London。

他们还发表了相关论文《Single Cortical Neurons as Deep Artificial Neural Networks》。

论文地址：https://www.sciencedirect.com/science/article/abs/pii/S0896627321005018

DeepMind 决策算法设计师 Timothy Lillicrap 认为，新的研究结果表明有必要重新思考将大脑神经元与机器学习领域神经元进行松散比较的旧传统了。

5 至 8 层人工神经元才能达到单个生物神经元的复杂度

人工神经元和生物神经元之间最基本的比较是它们如何处理传入的信息。这两种神经元都接收传入信号，并根据输入信息决定是否将信号发送给其他神经元。虽然人工神经元依赖简单的计算做出决定，但数十年的研究表明，生物神经元的这个过程要复杂得多。计算神经科学家使用输入 - 输出函数来模拟生物神经元树突接收到的输入与神经元发出信号之间的关系。

研究者让一个人工深度神经网络模仿输入 - 输出函数（生物神经元树突接收到的输入与神经元发出信号之间的关系），以确定其复杂性。他们首先对一种神经元的输入 - 输出函数进行了大规模模拟，这种神经元的顶部和底部有不同的树突分支，称为锥体神经元，来自大鼠的皮层。然后，他们将模拟结果输入到一个深度神经网络中，该神经网络每层最多有 256 个人工神经元。

接着，他们不断的增加层数，直到在模拟神经元的输入和输出之间达到毫秒级别 99% 的准确率。深度神经网络成功地预测了神经元的输入 - 输出函数的行为，所使用的层数至少有 5 层，但不超过 8 层。在大多数网络中，这相当于 1000 个人工神经元对应一个生物神经元。

如下图 2 所示，具有 7 个隐藏层、每层包含 128 个特征图的时间卷积网络（TCN）忠实地捕获了一个 L5PC （layer 5 pyramidal neuron）模型。

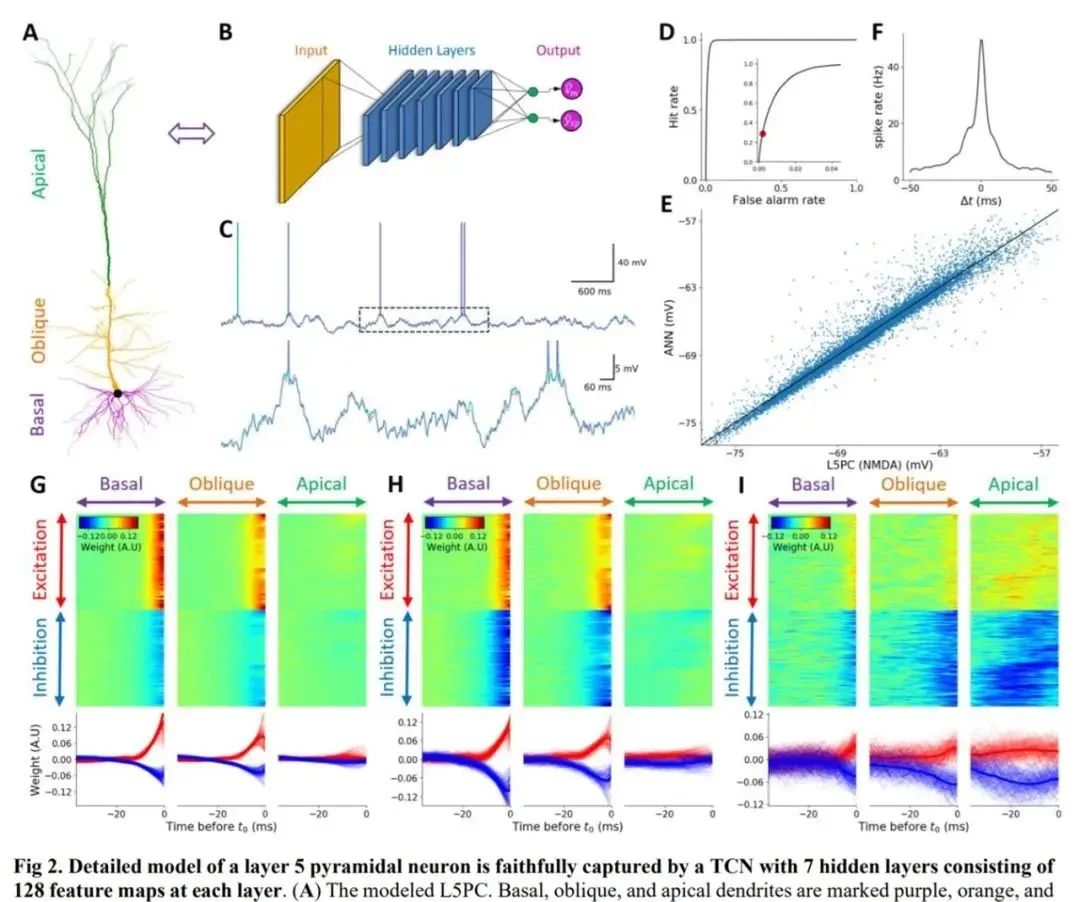
在下图 3 中，研究者展示了没有 N - 甲基天冬氨酸（NMDA）突触的 L5PC 神经元，它能够被具有单个隐藏层（包含 128 个隐藏单元）的深度神经网络忠实地捕获。其中 A 为 L5PC 模型示意图、B 为类比的深度神经网络。

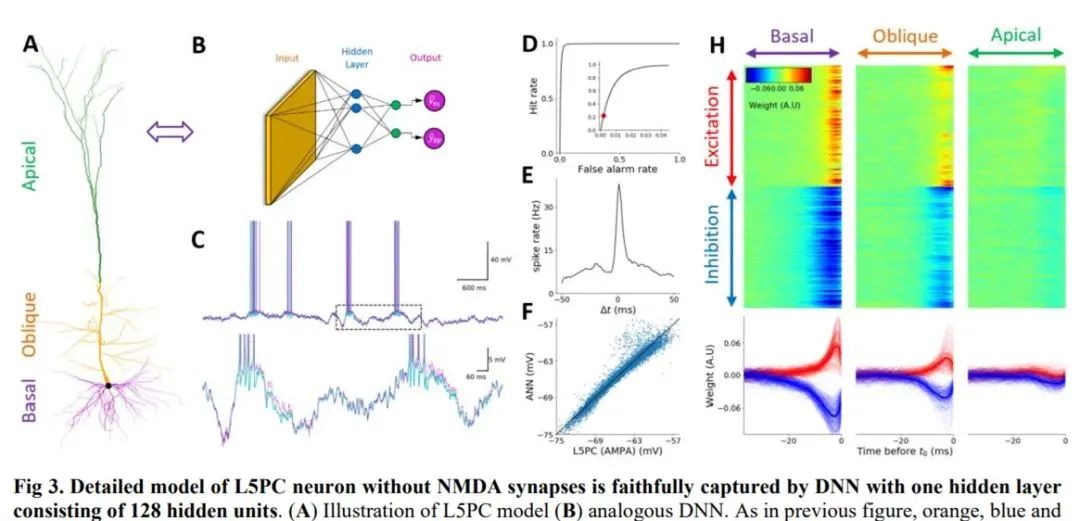
现在已经了解了单个神经元的计算复杂度，如下动图所示，左边的椎体神经元依赖树突状的分支，这些分支会受到信号的影响。在神经元决定是否发送 spike 信号之前，信号变化会导致局部电压变化，表现为神经元颜色的变化（红色表示高电压，蓝色表示低电压）。这一 spike 出现了 3 次，如右侧单个分支的轨迹所示，颜色代表树突从顶部（红色）到底部（蓝色）的位置。

来自贝勒医学院的计算神经科学家 Andreas Tolias 表示，这种结果建立了从生物神经元到人工神经元的桥梁。但研究者表示，这还不是一个直接的对应关系（生物神经元到人工神经元）。

Michael London 认为「神经网络中的层数与网络的复杂性之间的关系并不明显，所以我们不能说网络层数从四层增加到五层复杂度会增加多少。我们也不能说需要 1,000 个人工神经元就意味着生物神经元的复杂度恰好是生物神经元的 1,000 倍。最终，即使在每一层中使用指数级的人工神经元，最终也有可能形成只有一层的深层神经网络——但这可能需要更多的数据和时间来让算法学习。」

研究者尝试了很多架构，几乎都失败了。他们还公开了代码，以鼓励其他研究人员找到更少层的解决方案。但是，找到一种能够模仿神经元且准确率高达 99% 的深度神经网络是非常困难，研究者相信他们的结果为进一步的研究提供了有意义的比较。

Timothy  Lillicrap 认为，这可能提供了一种新的方法，将图像分类网络（通常需要 50 层以上）与大脑联系起来。如果每个生物神经元都像一个五层人工神经网络，那么一个 50 层的图像分类网络可能相当于一个生物网络中的 10 个真实神经元。

此外，该研究还希望他们的结果将改变 SOTA 人工智能深度网络架构。「我们呼吁替换深度网络技术，使其工作方式更接近大脑，这一实现过程是将深度网络中的每个简单单元替换为代表神经元单元，而这种神经元单元本身就是有深度的，」Segev 表示。在这种替代方案中，AI 研究人员和工程师可以插入一个五层深度网络作为「迷你网络」，用来取代每一个人工神经元。

各路专家学者如何看

但有些人怀疑这是否真的有利于 AI。「我认为这是一个悬而未决的问题，这种做法是否存在实际的计算优势，」来自冷泉港实验室的神经科学家 Anthony Zador 表示道。这项工作为测试奠定了基础。

除了 AI 应用之外，该研究还加深了人们对树突状树和单个神经元强大计算能力的共识。早在 2003 年，三名神经科学家展示了锥体神经元的树突树可以进行复杂的计算，通过将其建模为两层人工神经网络。在这项新研究中，研究者探索了金字塔神经元的哪些特征激发了 5 到 8 层深度神经网络的复杂性。他们得出结论，这来自树突树，树突表面接收化学信使的特定受体——这一发现与先前研究者在该领域的研究一致。

而一些人认为，这一结果意味着神经科学家应该把单个神经元的研究放在更重要的位置。「这篇论文使得对树突和单个神经元的思考比以前更加重要」，宾夕法尼亚大学计算神经科学家 Konrad Kording 说。另外还有一些人如 Lillicrap 和 Zador，它们认为关注回路中的神经元对于了解大脑如何实际利用单个神经元的计算复杂性同样重要。

无论如何，人工神经网络的语言可能为理解神经元和大脑的能力提供新的洞见。伦敦大学学院的计算神经科学家 Grace Lindsay 表示：「从层数、深度和宽度这几方面思考让我们对计算复杂度有了更直观的认识，不过这项研究仍然只是模型与模型之间的比较。」

遗憾的是，目前神经科学家无法记录真实神经元的完整输入 - 输出功能，因此生物神经元模型无法捕获到的信息可能更多。也就是说，真实神经元可能更加复杂。

Michael London 对此也表示：「我们并不确定 5 至 8 层是否就是最终数字。」

原文链接：

https://www.quantamagazine.org/how-computationally-complex-is-a-single-neuron-20210902/

高颜值免费 SCI 在线绘图(点击图片直达)

最全植物基因组数据库IMP (点击图片直达)

往期精品(点击图片直达文字对应教程)

机器学习