金融数据的尖峰厚尾特征是相比较标准正态分布来说的,标准正态分布的偏度为0,峰度为3,通常做实证分析时,会假设金融数据为正态分布,这样方便建模分析。但是实证表明,很多数据并不符合正态分布,而更像尖峰厚尾,就是峰度比3大,两边的尾巴比正态分布厚,没有下降得这么快。厚尾分布主要是出现在金融数据中,例如证券的收益率。 从图形上说,较正态分布图的尾部要厚,峰处要尖。直观些说,就是这些数据出现极端值的概率要比正态分布数据出现极端值的概率大。因此,不能简单的用正态分布去拟合这些数据的分布,从而做一些统计推断。一般来说,通过实证分析发现,自由度为5或6的t分布拟合的较好。
统计研究表明,大部分权益类金融产品的回报率的概率分布呈现出leptokurtic的特征。这种概率分布相对于标准正态分布,峰度更高,两段的尾部更厚,也就是极值更多的意思。
在统计学中,可以用峰度的计算公式。
以上公式计算的是kutosis excess,大于0即为高峰度,也就是尖峰厚尾。
尖峰厚尾是相比较标准正态分布来说的,标准正态分布的偏度为0,峰度为3,我们通常做实证分析时,会假设金融数据为正态分布,这样方便建模分析,但是实证表明,很多数据并不符合正态分布,而更像尖峰厚尾,就是峰度比3大,两边的尾巴比正态分布厚,没有下降得这么快。个人感觉,对于峰度和偏度的研究不是很多,关键是自己心里有尖峰厚尾这个概念最重要。希望对你有帮助!
金融数据的尖峰厚尾
最新推荐文章于 2025-01-13 15:12:58 发布








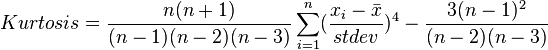


















 251
251

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








