1/4波长阻抗变换器

首先看一个问题，如下图在RL≠Z0的前提下怎么能阻抗匹配呢：

为了解决这个问题，我们增加一段长为L的传输线来尝试进行匹配：

由于传输线和终端负载ZL有反射，则根据反射理论，传输线L任意位置的电压和电流可以描述为：

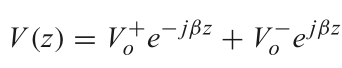
其中V0+代表前向传输的电压，V0-代表反射回来的电压，至于β=2π/波长；

同时我们可以知道反射系数为：

化简电压电流公式为：

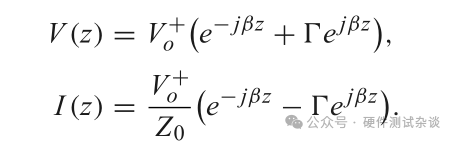
要想阻抗匹配，则需要在-L处阻抗等于输入阻抗Zin。公式如下：

然后利用欧拉公式化简：

从上式子可以看出，当L的是长度是1/4波长的奇数倍时：

到这就结束了，结论就是使用阻抗为根号下（Zin*ZL）且长度为1/4波长的传输线，达到了阻抗完全匹配。

但是，是否还有一个疑问，阻抗明明不相等，怎么就匹配了呢，没有反射吗？ 来看下仿真吧，首先搭建一个仿真，输入1GHz的正弦波，理想传输线1/4波长，内阻20Ω，负载80Ω，计算传输线阻抗为40Ω：

仿真结果来看比较完美匹配，正弦波幅值变成了原波形的一半：

为啥没有反射呢，明明三段阻抗不一样的？那我们再看下这个从零时刻起始的仿真结果，可以看到起始过程是有反射的，Vo的振幅开始不是0.5V，但会逐渐降低直到稳定：

现在又来一个问题，这个阻抗变换器适用于信号匹配吗？那再来看下S参数仿真，如下：

从S参数来看，明显奇数倍的倍频存在谐振点，符合之前推出的1/4波长奇数倍阻抗匹配的结果。另外谐振点只是一个点，有效带宽比较窄，因此不适用信号的匹配，基本只能用于射频匹配（原因是射频基本关注很窄频带的信号，而高速信号的带宽很宽）。

另外还有一个问题，就像刚才从零时刻仿真结果，发现信号稳定需要一定的时间，期间反射比较大影响性能怎么办，其实还有多段匹配的方法，理论和1/4波长一样，只不过从一段匹配改成了阶梯匹配，从而使每段阻抗之间更相近，反射也更小，代价的话就是线太长，不太实用。