单频阻抗匹配：采用四分之一波长变换器

最新推荐文章于 2023-09-08 10:56:41 发布

南贝塔

最新推荐文章于 2023-09-08 10:56:41 发布

阅读量5.9k

点赞数 6

分类专栏：射频文章标签：射频

本文链接：https://blog.csdn.net/snsb_csdn/article/details/124075242

版权

射频专栏收录该内容

6 篇文章

订阅专栏

本文详细介绍了传输线理论中的阻抗匹配概念，包括共轭匹配和实数阻抗匹配。通过四分之一波长变换器，可以实现实数负载与传输线的阻抗匹配。对于复数阻抗的负载，通过并联终端短路或开路的短截线，可以将其转换为实数阻抗，再利用四分之一波长变换器进行匹配。这种方法仅适用于单频阻抗匹配，适用于特定频率的射频网络设计。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 什么是阻抗匹配

在传输线理论中，考虑一段特征阻抗为 $Z_0$ 的传输线，其终端连接一个阻抗为 $Z_L$ 的负载。

001

若两个阻抗为复数：
$Z_0=R_0+jX_0\tag{1a}$

$Z_L=R_L+jX_L\tag{1b}$

当 $Z_0$ 和 $Z_L$ 实部相等、虚部相反时，传输线与负载即实现阻抗匹配，这种情况称为“共轭匹配”：
$R_0=R_L\tag{2a}$

$X_0=-X_L\tag{2b}$

若两个阻抗为实数，那么当两个实数阻抗相等，即 $Z_0=Z_L$ 时，传输线与负载即实现阻抗匹配。

那么，当传输线与负载阻抗不匹配时，会发生什么呢？

002

考虑一个正弦信号 $V_0^+e^{-j{\beta}z}$ 从 $z < 0$ 入射到这个由传输线中。当信号在传输线上传播时，信号的幅值为 $V (z)$ ，传输线上相应的电流为 $I (z)$ ，它们的比值即为传输线的特征阻抗 $Z_0$ ；而当信号到达负载时，信号幅值和电流的比值则为负载阻抗 $Z_L$ ，在 $z = 0$ 处的阻抗产生不连续性，此时传输线上将产生一个反射信号来使 $z = 0$ 处的阻抗条件得到满足。因此，传输线和负载阻抗不匹配导致会信号反射。

解决这个问题的方法是，在传输线与负载之间加入一个阻抗匹配网络（Impedance Matching Network），来使从传输线看向匹配网络时的阻抗为 $Z_0$ ，这样，传输线上的信号反射可以被消除。不过，匹配网络与负载之间仍会存在信号反射的。

003

对射频网络进行「阻抗匹配」，就是设计阻抗匹配网络的结构和参数，从而实现消除传输线反射的目标。目前比较方便地进行阻抗匹配的方法有计算机仿真、利用 Smith 圆图图解等。与这些方法相比，手工推导阻抗匹配网络解析解的方法比较繁琐，不过应对一些简单的阻抗匹配问题还是游刃有余的。

今天就来手工推导一个单频阻抗匹配网络，也就是在单一频率上，让一个具有任意阻抗的负载与具有实数阻抗的传输线实现匹配。可以实现匹配的网络结构有多种，今天我们采用四分之一波长变换器 (The Quarter-wave Transformer)。

四分之一波长变换器是指一段长度等于传输信号波长的四分之一的传输线，它是一种简单实用的单频点阻抗匹配电路。为什么叫「变换器」呢，下文会给出解释。

2. 传输线阻抗方程

推导阻抗匹配问题一定会涉及到的一个公式是传输线阻抗方程 (Transmission Line Impedance Equation)。它的含义是，当一段阻抗为 $Z_0$ 、长度为 $l$ 的传输线终端连接着阻抗为 $Z_L$ 的负载时，两者构成了一个网络：

004

看向这个网络的输入阻抗 $Z_{in}$ 将不再是 $Z_0$ 。 $Z_{in}$ 变为：
$Z_{in}=Z_0\cdot\frac{Z_L+jZ_0{\rm tan}{\beta}l}{Z_0+jZ_L{\rm tan}{\beta}l}\tag{3}$

其中， $\beta=2\pi/\lambda$ ， $\lambda$ 为在网络中传播的信号波长。

详细推导可以戳。

3. 实数阻抗匹配

首先来讨论负载的阻抗为实数时的阻抗匹配。负载阻抗为 $Z_L$ ，传输线的阻抗为 $Z_0$ ，作为阻抗匹配网络的四分之一波长变换器的阻抗为 $Z_1$ ，长度是传播的信号波长的1/4。我们的任务就是找到合适的 $Z_1$ 值，令负载与传输线的阻抗匹配。

005

根据式(3)，看向阻抗匹配网络的输入阻抗 $Z_{in}$ 可以表示为：
$Z_{in}=Z_1\cdot\frac{Z_L+jZ_1{\rm tan}{\beta}l}{Z_1+jZ_L{\rm tan}{\beta}l}\tag{4}$
等号右侧分子分母同除以 $tan{\beta}l$ ，得：
$Z_{in}=Z_1\cdot\frac{\frac{Z_L}{{\rm tan}{\beta}l}+jZ_1}{\frac{Z_1}{{\rm tan}{\beta}l}+jZ_L}\tag{5}$
其中：
${\rm tan}{\beta}l={\rm tan}\frac{2π}{\lambda}·\frac{\lambda}{4}={\rm tan}\frac{π}{2}\rightarrow\infty\tag{6}$
因此，式(5)可以简化为：
$Z_{in}=Z_1·\frac{jZ_1}{jZ_L}=\frac{Z_1^2}{Z_L}\tag{7}$
式(7)直观地展示了四分之一波长变换器的特性，它将阻抗从 $Z_L$ 变换为 $Z_1^2/Z_L$ ，故称「变换器」。为了实现阻抗匹配，令 $Z_{in}=Z_0$ ，则有：
$Z_1=\sqrt{Z_0Z_L}\tag{8}$
因此，我们只需要让传输线与阻抗之间的四分之一波长变换器的阻抗按式(8)取值，即可使实现将实数负载阻抗匹配至传输线。

4. 复数阻抗匹配

现在来讨论更具一般性的情况，即传输线的阻抗为实数，而负载的阻抗为复数时的阻抗匹配，此时 $Z_L=R_L+jX_L$ 。四分之一波长变换器只能匹配实数阻抗至传输线，我们的思路是设法将负载的复数阻抗转换为实数阻抗，这可以通过在四分之一波长变换器和负载之间并联终端短路或开路的短截线来实现。

006

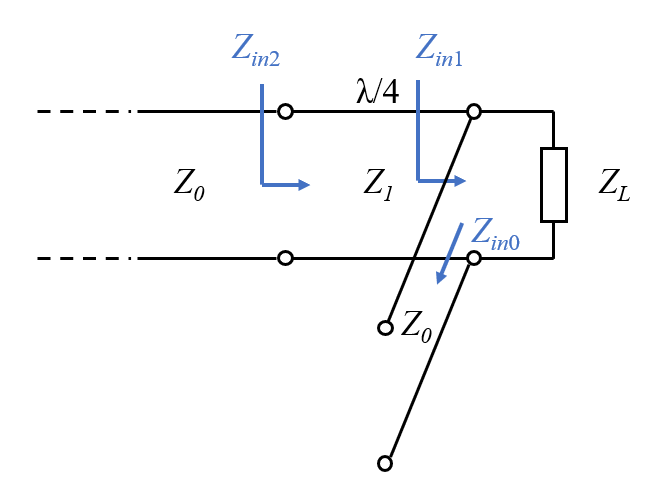
终端短路的短截线相当于终端连接了阻抗等于0的负载，根据式(3)，终端短路短截线的输入阻抗 $Z_{in·short}$ 可以表示为：
$Z_{in·short}=Z_0\cdot\frac{0+jZ_0{\rm tan}{\beta}l}{Z_0+j0{\rm tan}{\beta}l}=jZ_0{\rm tan}{\beta}l\tag{9}$
因此，终端短路的短截线的输入阻抗为纯虚数，且可以取 $-j\infty$ 至 $+j\infty$ 之间的任意值。

终端开路的短截线则相当于终端连接了阻抗无穷大的负载，同样可以推导得到其输入阻抗为：
$Z_{in·open}=-jZ_0{\rm cot}{\beta}l\tag{10}$
其输入阻抗也为纯虚数，且可以取 $-j\infty$ 至 $+j\infty$ 之间的任意值。

回到图中，负载阻抗 $Z_L=R_L+jX_L$ ，将其转换为导纳形式：
$Y_L=G_L+jB_L\tag{11}$
并联的终端开路短截线的输入阻抗 $Z_{in0}=-jZ_0{\rm cot}{\beta}l$ ，同样将其转换为导纳形式：
$Y_{in0}=-jB_0\tag{12}$
此时，看向负载与短截线并联网络的输入导纳 $Y_{in1}=Y_L+Y_{in0}$ 。通过对短截线取合适的长度，总可以使 $B_0=B_L$ ，将负载阻抗的虚部抵消，从而实现将负载的复数阻抗变换为实数阻抗：
$Y_{in1}=Y_L+Y_{in0}=G_L+jB_L-jB_0=G_L\tag{13}$
转回阻抗形式：
$Z_{in1}=R_L\tag{14}$
接下来就是熟悉的路子了，参考式(4)-(7)，经过四分之一波长变换器的输入阻抗 $Z_{in2}$ 表示为：
$Z_{in2}=\frac{Z_1^2}{R_L}\tag{15}$
为了实现阻抗匹配，令 $Z_{in2}=Z_0$ ，则有：
$Z_1=\sqrt{Z_0R_L}\tag{16}$
这样，通过并联终端开路短截线和四分之一波长变换器，就将复数负载阻抗匹配至传输线了。我们也可以将终端开路短截线替换为终端短路短截线，在实际应用中，视两种短截线的加工难易程度决定。