特征提取算法

0. 写在前边

本篇将介绍几种特征提取算法，特征提取算法的本质是从数据中找出具有特定特征或者信息的部分，并将其表示为更简单、更易于处理的形式。这里将介绍图像处理中的Harris，SUSAN和SIFT(Scale-Invariant Feature Transform)算法，点云处理中的ISS(Intrinsic Shape Signatures)

特征点是在图像处理和点云中具有特定特性的点。1）在图像处理中，特征点通常是指图像中具有显著变化或者重要信息的位置，比如角点、边缘点、纹理点等。这些点通常被用来进行图像配准、目标跟踪、物体识别等任务，因为它们能够提供重要的位置和结构信息。2）在点云中，特征点指的是具有显著几何特性的点，比如曲率变化明显的点、表面法向变化明显的点、高度变化大的点等。这些特征点在点云处理中非常重要，可以用来进行点云配准、目标检测、三维重建等任务，因为它们能够提供点云的关键几何信息。

1. Harris算法

1.1 写在前面

Harris角点检测算法是一种经典的图像特征检测算法，用于在图像中检测角点，即具有显著变化的位置，暂时可以理解为角点(Corner点)。一张图片中的点，在某个尺度上进行划分，可以划分为"flat"点，“edge"点和"corner"点，这三种点的直观理解参见下图:

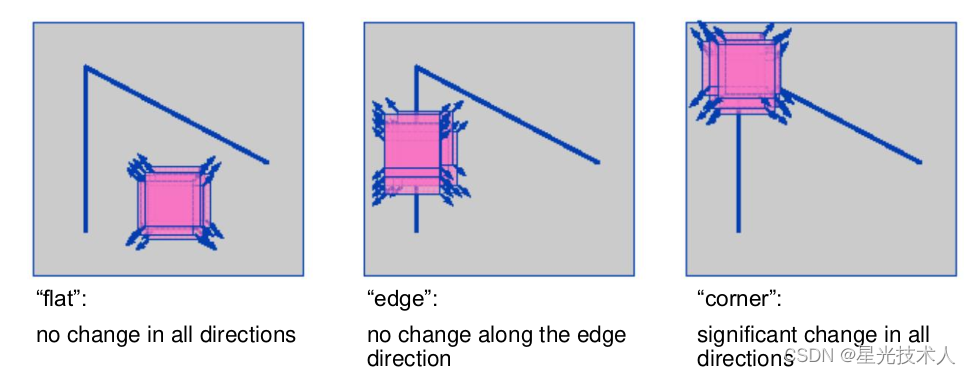
直观上来理解，给你一张图，让你来标出你认为的几个"独特"点，我想大概率你会标出与周围邻域内像素点的“颜色"或者"形状"反差较大的点吧。这里用到的“颜色“和“形状“就是上文说的尺度。
在Harris算法中，也是这种思想，记像素点$(x,y)$处的特征(多使用颜色值)为$I(x,y)$。选用移动值$({\delta }_x,{\delta }_y)$计算像素点$(x,y)$处的颜色值变化为$I(x,y)-I(x+{\delta }_x,y+{\delta }_y)$，也可以理解为$(x,y)$处的梯度，但因像素点位置空间是离散的，因此采用差分的方式表达变化率。 设想一下，给你一张1200*900分辨率的图片，你能比较出一个像素点与周围像素点的区别？比较单个像素点，不仅耗时而且对噪声点也不够鲁棒，所以Harris算法中，是选用的一个"path”,也就是一小片区域$\Omega$，用这个区域在移动前后的颜色值变化记为:
$$E(u,v)=\sum _{x,y\in \Omega }w(x,y)[I(x+u.y+v)-I(x,y){]}^2$$其中，$(u,v)$是offset，代表区域$\Omega$的移动，就是求梯度时的增量。$w(x,y)$是权重，代表区域$\Omega$内像素点的梯度给区域中心点的贡献度，多采用下图右侧高斯分布的形式。

到这里，就已经完成了问题的定义，给定一张图片，Harris算法就是通过每个像素位置$(x,y)$的$E(u,v)$来判断该位置是否为特征点，是什么类型的特征点。

1.2 Harris算法的本质

承接上文,$E(u,v)$可以作如下推导:
$$\begin{array}{rl}E(u,v)& =\sum _{x,y\in \Omega }(I(x+u,y+v)-I(x,y){)}^2\\ E(u,v)& =\sum _{x,y\in \Omega }(I(x,y)+u{I}_x(x,y)+v{I}_y(x,y)-I(x,y){)}^2\\ E(u,v)& =\sum _{x,y\in \Omega }{u}^2{I}_x^2+v^2{I}_y^2+2uv{I}_x{I}_y\\ E(u,v)& =\left[\begin{array}{cc}u& v\end{array}\right](\sum _{x,y\in \Omega }\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right])\left[\begin{array}{c}u\\ v\end{array}\right],M=\sum _{x,y\in \Omega }\left[\begin{array}{cc}{I}_x^2& I_x{I}_y\\ I_x{I}_y& I_y^2\end{array}\right]\\ E(u,v)& =\left[\begin{array}{cc}u& v\end{array}\right]M\left[\begin{array}{c}u\\ v\end{array}\right]\end{array}$$

可见，已经将$E(u,v)$转化为了谱定理的形式，也就是说这个区域$\Omega$移动前后的特征变化可以用区域内所有像素点的颜色梯度$I_x,I_y$的分布来表示，见下图

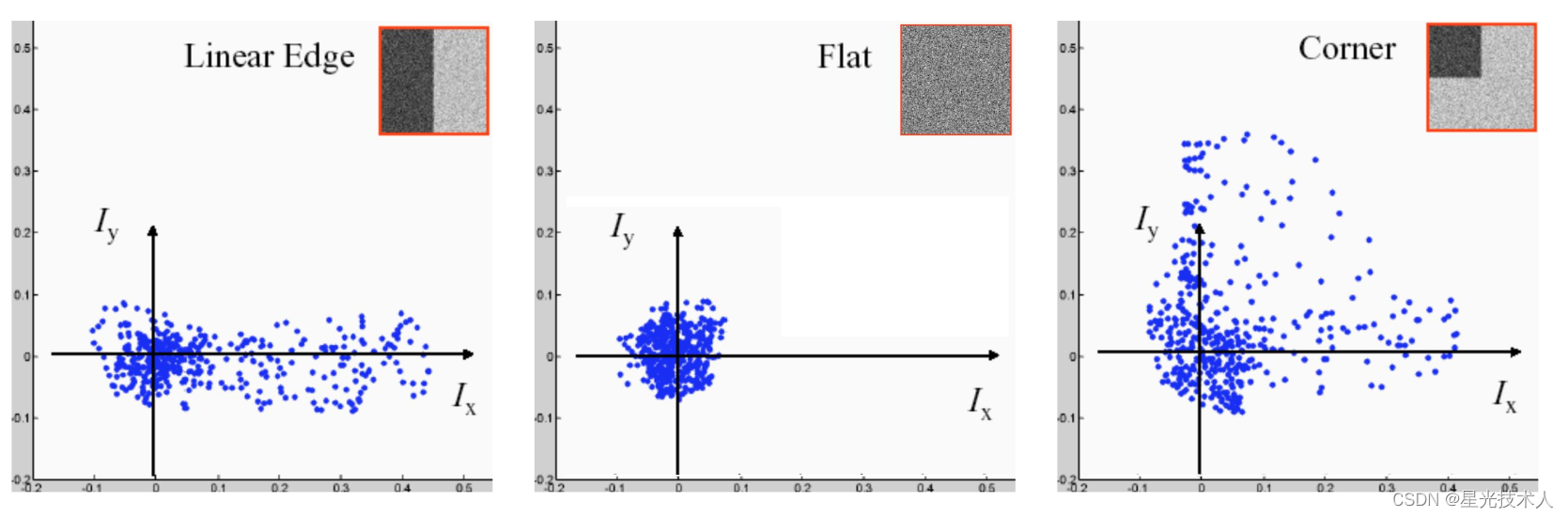
记矩阵$M$的特征值为${\lambda }_1,{\lambda }_2$。“flat“点均为0，"edge"点其中一个为零,"corner"两者均不为零。因此Harris的本质就是求某点周围邻域内所有点的颜色颜色梯度构成的协方差均值的特征值。

1.3 Harris算法的简化

承接上文，得到矩阵$M$的特征值以后，特征值的阈值怎么设置?，如果有多个特征值，怎么来判断这个点是否维特征值?1988年，1994年1998年，三位作者给出了特征值Response的三种不同计算方法，使用Pesponse值来代表所有特征值，通过Response值的阈值直接判断是否为特征点。

在使用Harris算法的时候，如果Response阈值设置的比较小，就会造成特征点太多的问题，这个时候可以采用NMS算法的思想进行去重。1）首先找到R值最大的特征点，删除周围邻域r内的特征点。然后重复步骤1）。结果实例如下:

阶段	结果
原始图片
Harris处理
NMS处理

2. Harris3D

Harris3D算法是Harris2D的推广，也就是Harris算法从图像处理到点云处理的转化。承接上文，Harris算法应用在3D点云中需要明确几个问题:

• 1. 点云是离散的
• 2. 点云中的"patch"也就是2D图像中的区域$\Omega$怎么选取
• 3. 如何移动"patch"

针对1，与2D图像中的像素点都是离散的，只不过点云是稀疏的，并不是每个位置都有点。
针对2，在2D图片中，通过领域来确定某个点的邻域空间$\Omega$。
针对3，在2D图片中，通过增量$(u,v)$来完成patch的移动，求得像素点的梯度$I_x,I_y$。在3D点云中，$I_x,I_y,I_z$应该怎么求解？

2.1 Harris3D算法问题定义

记点$P(x,y,z)$周围的小邻域为$\Omega$, 点$P$的激光反射强度为$I(x,y,z)$,增量记为$(u,v,w)$,则增量前后区域$\Omega$的反射强度变化为:
$$E(u,v,w)=\sum _{u,v,w\in \Omega }[I(x+u,y+v,z+w)-I(x,y,z){]}^2$$
进一步推导得,
$$\begin{array}{rl}E(u,v,w)& =\sum _{x,y,z\in \Omega }[u{I}_x(x,y,z)+v{I}_y(x,y,z)+w{I}_z(x,y,z){]}^2\\ & =\left[\begin{array}{ccc}u& v& w\end{array}\right](\sum _{x,y,z\in \Omega }\left[\begin{array}{ccc}{I}_x^2& I_x{I}_y& I_x{I}_y\\ I_x{I}_y& I_y^2& I_y{I}_z\\ I_x{I}_z& I_y{I}_z& I_z^2\end{array}\right])\left[\begin{array}{c}u\\ v\\ w\end{array}\right],M=\sum _{x,y\in \Omega }\left[\begin{array}{ccc}{I}_x^2& I_x{I}_y& I_x{I}_y\\ I_x{I}_y& I_y^2& I_y{I}_z\\ I_x{I}_z& I_y{I}_z& I_z^2\end{array}\right]\\ & =\left[\begin{array}{ccc}u& v& w\end{array}\right]M\left[\begin{array}{c}u\\ v\\ w\end{array}\right]\end{array}$$
其中，$I_x,I_y,I_z$就为某位置在对应尺度上三个方向的梯度，图像中尺度可以选择颜色空间，但是点云中即可以使用反射强度尺度，也可以选择空间位置尺度。使用空间位置的尺度的话，Harris3D求出的特征点就是几何空间的特征点。下边将分别介绍以反射强度为尺度和以空间位置尺度的Harris 3D算法。称为Harris3D with Intensity和Harris3D without Intensity。

2.2 Harris3D with intensity

结合harris2d算法的理解，重点还在求出区域$\Omega$内所有点在三个方向上的反射强度梯度构成的协方差矩阵M的特征值，图像中$I_x,I_y$可以通过差分的方式求解，在3D点云中，邻域中心点P还在反射强度尺度上的$I_x,I_y和I_z$需要怎么求出来；因为点云的稀疏特性，不能单纯使用增量完成差分求解。

• 最小二乘法
  选定点P和点云的邻域r范围$\Omega$。使用最小二乘法完成，邻域内点的平面拟合(这个平面需要最能拟合所有点反射强度值，也就是说函数自变量为坐标位置，函数值为反射强度)，拟合平面的法向量$e=[I_x,I_y,I_z]$即为所求。
  不过请注意，这是在邻域内点的反射强度空间上求出的值，很有可能会被点P旁边的某个点带偏，所以在使用最小二乘法得到基础的$I_x,I_y,I_z$后，还要做个处理。
  记坐标位置点$p(p_x,p_y,p_z)$，邻域$\Omega$内点的坐标位置是$p_i=[x_i,y_i,z_i]$,点p处的反射强度梯度变化为$e=[e_x,e_y,e_z]$.构建等式，
  $$\left(x_i-p_x\right)e_x+\left(y_i-p_y\right)e_y+\left(z_i-p_z\right)e_z=I\left(x_i,y_i,z_i\right)-I\left(p_x,p_y,p_z\right)$$
  向量表示：
  $$\begin{array}{l}{\mathbf{x}}_i^{\prime T}\mathbf{e}=\Delta I_i\\ {\mathbf{x}}_i^{\prime }={\left[x_i^{\prime },y_i^{\prime },z_i^{\prime }\right]}^T={\left[x_i-p_x,y_i-p_y,z_i-p_z\right]}^T\end{array}$$
  矩阵表示，
  $$A\mathbf{e}=\mathbf{b},A=\left[\begin{array}{ccc}{x}_1^{\prime }& y_1^{\prime }& z_1^{\prime }\\ ⋮& ⋮& ⋮\\ x_i^{\prime }& y_i^{\prime }& z_i^{\prime }\\ ⋮& ⋮& ⋮\end{array}\right],\mathbf{b}=\left[\begin{array}{c}\Delta I_1\\ ⋮\\ \Delta I_i\\ ⋮\end{array}\right]$$
  因此，要求解$e=[e_x,e_y,e_z]$的优化函数为:
  $$\underset{\mathbf{e}}{\min }\Vert A\mathbf{e}-\mathbf{b}{\Vert }_2^2$$得，$$e=(A^{T}A{)}^{-1}{A}^{T}b$$上文提到，求出的e方向会被点周围的点噪声点带跑偏，所以需要求出点p邻域$\Omega$内点的法向量，完成e的优化。$$e^{{}^{\prime }}=e-n(n{n}^T)=e-n(e^{T}n)$$其中，法向量n可以有PCA算法求解。
  

综上，就可以得到Harris 3D with intensity算法中，点p的反射强度梯度$[I_x,I_y,I_z]$的求解，然后进一步求出反射强度梯度构成的协方差矩阵的特征值，就能算出点p是否为特征点(在反射强度空间)。

2.3 Harris3D without intensity

不考虑反射强度的前提下，3D点云的harris特征点，可以直接通过点云的法向量$(n_x,n_y,n_z)$求解。构建邻域范围内点的法向量的协方差矩阵，计算协方差矩阵的特征值即可。
Harris3D without intensity和Harris3D with intensity两种尺度下，判读点是否特征点的策略如下:

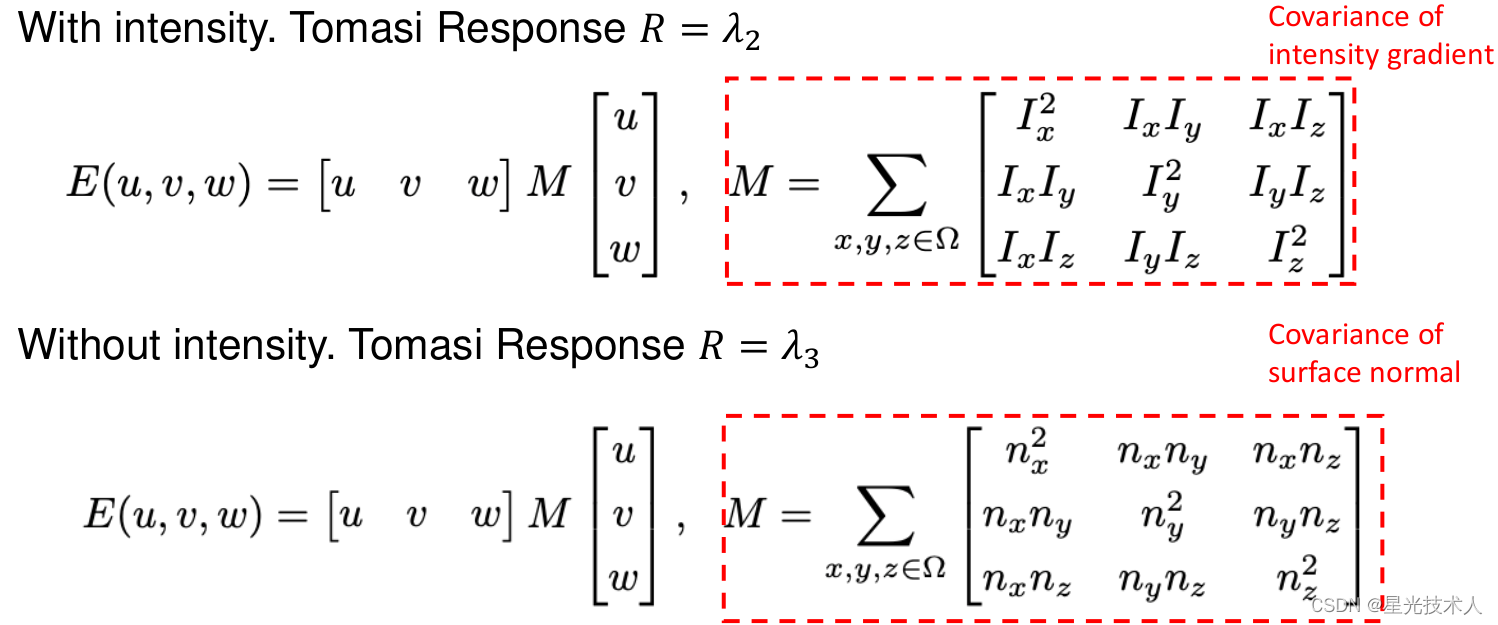
如果，需要综合考虑反射强度和空间位置来进行harris特征点的判断，就需要一个包含发射强度梯度和法向量的协方差矩阵，并且Response值的判读也更为复杂，请看下图:

$$\begin{array}{lllll}& \text{ Input }& \text{ Covariance Matrix }& \text{ Criteria }& \text{ Intuition }\\ \text{ Harris Image }& \text{ Image }& \text{ Intensity gradient }& {\lambda }_2\text{ is small }& \text{ Intensity corners }\\ \text{ Harris 3D }& \text{ PC with Intensity }& \text{ Intensity gradient }& {\lambda }_2\text{ is small }& \text{ Intensity corners in local surface }\\ \text{ Harris 3D }& \text{ PC }& \text{ Surface normals }& {\lambda }_3\text{ is small }& \text{ Corners in 3D space }\\ \text{ Harris 6D }& \text{ PC with Intensity }& \begin{array}{l}\text{ Intensity gradient }+\\ \text{ surface normals }\end{array}& {\lambda }_4\text{ is small }& \begin{array}{l}\text{ Corners in either 3D space / }\\ \text{ local surface intensity }\end{array}\end{array}$$

3. ISS

Harris3D算法是从2D图片的hsrris算法延伸而来的，ISS算法是3D点云原生特征点提取算法，思路与Harris 3D without intensity的思路类似。只不过ISS算法中的空间位置协方差矩阵使用了距离权重，Harris3D没有使用距离权重。

写不动了

$$\begin{array}{lllll}& \text{ Input }& \text{ Covariance Matrix }& \text{ Criteria }& \text{ Intuition }\\ \text{ Harris Image }& \text{ Image }& \text{ Intensity gradient }& {\lambda }_2\text{ is small }& \text{ Intensity corners }\\ \text{ Harris 3D }& \text{ PC with Intensity }& \text{ Intensity gradient }& {\lambda }_2\text{ is small }& \text{ Intensity corners in local surface }\\ \text{ Harris 3D }& \text{ PC }& \text{ Surface normals }& {\lambda }_3\text{ is small }& \text{ Corners in 3D space }\\ \text{ Harris 6D }& \text{ PC with Intensity }& \begin{array}{l}\text{ Intensity gradient + }\\ \text{ surface normals }\end{array}& {\lambda }_4\text{ is small }& \begin{array}{l}\text{ Corners in either 3D space / }\\ \text{ local surface intensity }\end{array}\\ \text{ ISS }& \text{ PC }& \begin{array}{l}\text{ Weight point }\\ \text{ coordinates }\end{array}& \frac{{\lambda }_i^2}{{\lambda }_i^1}<{\gamma }_{21},\frac{{\lambda }_i^3}{{\lambda }_i^2}<{\gamma }_{32}& \begin{array}{l}\text{ Point distribution is different in }\\ \text{ 3 dimensions }\end{array}\end{array}$$

特征点的应用

在图片和点云中，特征点可以应用在二维图像驱动三维物体，提取视频中人脸的特征点对应在三维空间中的脸上，就可以实现动画人表情的变换。两者需要二维到三维的转换关系。

• 图像处理：在图像处理中，特征点常用于物体识别、图像配准、运动跟踪等任务。比如在人脸识别中，特征点可以用来标记面部的关键特征，帮助识别不同的人脸；在图像配准中，特征点可以用来匹配不同图像之间的对应位置，实现图像的对齐和融合。
• 计算机视觉：在计算机视觉领域，特征点被广泛应用于目标检测、目标跟踪、三维重建等任务。比如在自动驾驶中，特征点可以用来识别道路标志、车辆等目标，帮助车辆进行导航和避障。
• 点云处理：在点云处理中，特征点常用于点云配准、场景分割、物体识别等任务。比如在工业领域，特征点可以用来检测和识别工件表面的缺陷或者特定形状，帮助质检和生产。
• 机器学习：在机器学习中，特征点可以作为输入数据的重要特征之一，用于训练模型和进行预测。比如在文本分类中，特征点可以是文本中的关键词或者短语，用来区分不同类别的文本。