SAR成像学习（三）距离方向成像matlab代码解析 1

本文将结合matlab代码讲解SAR距离向成像问题。
本文只研究距离向，且是正侧视情况。
文中以同一方位向坐标上四个目标点的成像为例，这四个目标的关系如下：

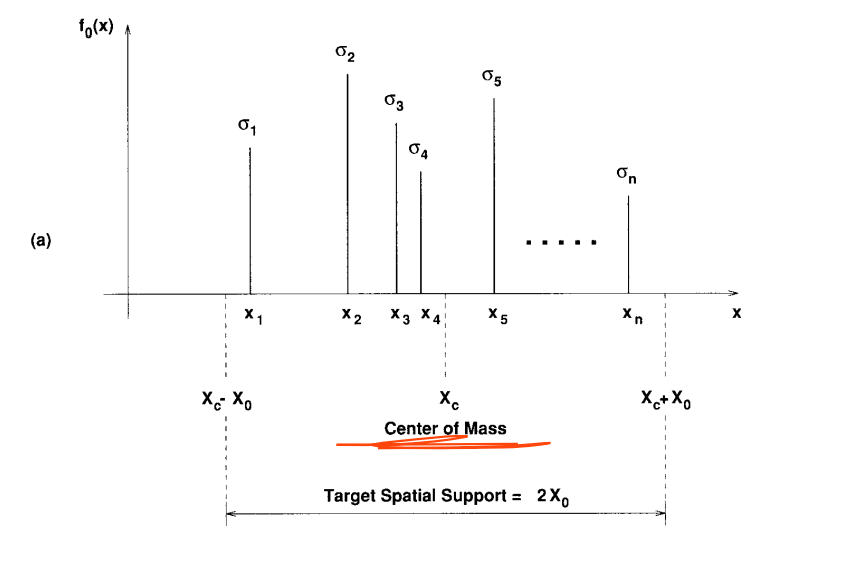
目标的相关信息：

% 关于目标
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Xc=2.e3;                 % Range distance to center of target area
X0=50;                   % target area in range is within [Xc-X0,Xc+X0]
ntarget=4;                        % number of targets
%%%%%%%%%%%%% Targets' parameters  %%%%%%%%%%%%%%%%%%
%
% xn: range;               fn: reflectivity 发射系数
%
xn(1)=0;                   fn(1)=1;
xn(2)=.7*X0;               fn(2)=.8;
xn(3)=xn(2)+2*dx;          fn(3)=1.;
xn(4)=-.5*X0;              fn(4)=.8;
%注意这里的xn是相对于中间的Xc的位置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

发射信号是线性调频信号：

% 关于发射信号
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
colormap(gray(256))
cj=sqrt(-1);
pi2=2*pi;
%
c=3e8;                   % Propagation speed
B0=100e6;                % Baseband bandwidth is plus/minus B0 注意这里的带宽是2B0
w0=pi2*B0;
fc=1e9;                  % Carrier frequency
wc=pi2*fc;

Tp=.1e-6;               % Chirp pulse duration

alpha=w0/Tp;             % Chirp rate
wcm=wc-alpha*Tp;         % Modified chirp carrier 即是式子中的beta
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

1 问题的描述

成像的过程只要分为两步： 发射信号到接收信号；后处理，即接收信号到影像 如图：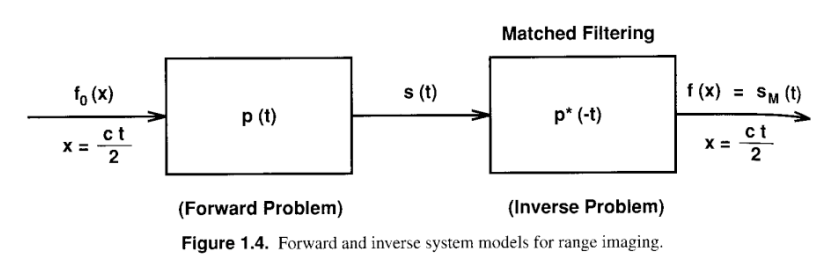

第一步是个正问题，主要由硬件完成，第二步是个逆问题，主要由软件完成。
第一个问题的输入$f_0(x)$是地面目标的理想函数，其与发射信号$p(t)$的联合起来之后得到输c出：回波信号$s(t)$。
第二个问题的输入是$s(t)$，通过与$p^{*}(-t)$匹配滤波，得到输出$f(x)$。这个输出就是我们想要的。如何得到$f(x)$就是我们的核心问题。
理想情况下$f(x) = f_0(x)$，这意味着我们得到了地面目标函数，也即是我们的影像完全真实地反映了地面的情况。但是，这是不可能实现的。不过，通过合理地解这个逆问题，使得$f(x)$接近$f_0(x)$是成像的关键问题，也是我们不断努力的目标。

2 问题的分析和解决

其实问题的解决办法在上一个图中已经暗示了，他就是匹配滤波技术，这个技术我们已经在“急救箱系列”分析过了。但是面对实际问题，还是有许多问题需要说明，尤其是像我这样的新手。

2.1 再谈匹配滤波

匹配滤波的实施公式：
$$S_M(t) = F_{(\omega)}^{-1}[S(\omega)P^{*}(\omega)]$$
其中$S(\omega),P(\omega)$分别为回波信号 s(t)