Friedman检验和Nemenyi检验，测试以及python实现

为了将不同的学习算法的泛化性能进行全面的比较，光靠学习器对某个数据集上的性度度量是不够的，我们需要用到假设检验，它为我们进行学习算法的比较提供了重要依据。

同时对于学习算法的比较，我们一般需要在多个数据集上比较多个算法的性能，这里常常采用Friedman检验和Nemenyi检验来进行比较。

1.Friedman检验

对于k个算法和N个数据集，首先得到每个算法在每个数据集上的测试性能结果，然后根据性能结果有好到坏排序，并给出序值1, 2, …, k，若多个算法性能结果相同，则它们平分序值，假设第i个算法的平均序值为ri，则ri服从正态分布：

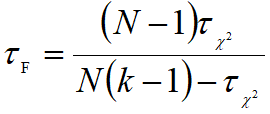
 则变量tF服从自由度为k-1和(k-1)(N-1)的F分布，假设这k个算法在N个数据集上的性能没有差异，若假设检验拒绝这个假设，则说明算法的性能显著不同，这时需要进行后续检验进一步区分各算法。

这里是Friedman的python实现：

2.Nemenyi检验

Nemenyi检验计算出平均序值差别的临界值域CD:

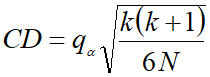
的值可以查看下表获得：

如果任意两个算法的序值差大于CD，则这两个算法性能有明显差异。

根据不同算法的结果排序，我们还可以进一步做Friedman图：

下面是我在十个数据集上调用sklearn库进行的测试（代码放在github上：https://github.com/aBadCat/machineLearning/tree/master/Friedman%26Nemenyi）：

未调参之前各算法在十个数据集上的MSE值如下表：

	liner	ridge	lasso	EN	CART	SVR	GBDT
Data1	28.727	5.191	7.25	6.19	3.257	8.142	2.997
Data2	3.646	0.074	0.267	0.267	0.001	0.044	0.001
Data3	36.383	12.555	13.418	11.875	18.082	11.267	18.308
Data4	0.353	0.351	0.689	0.652	0.648	0.322	0.355
Data5	4.858	4.862	6.965	7.087	5.293	5.325	3.596
Data6	50.778	50.189	40.724	49.422	306.841	292.39	93.912
Data7	12.441	12.478	15.951	21.108	0.596	9.606	0.333
Data8	14.304	14.285	17.417	21.966	8.909	13.098	3.388
Data9	50.235	50.303	54.811	54.898	74.02	51.911	48.373
Data10	19.431	13.902	25.132	35.311	44.726	46.255	14.458

 

计算得出Friedman值为2.237070295093028， 大于F分布对应自由度（7，42）的值2.237070295093028

画出Friedman图如下

对于Friedman图，如果两个算法没有重叠区域，则证明两个算法有明显差异。可以看到未调参前gbdt和弹性网络有很大的性能差别。