LOG,Harris,SUSAN角点及边缘检测原理和代码实现

目录：

一、 LOG算子

二、Harris算子

三、SUSAN算子

一、LOG算子

LOG算子：是高斯和拉普拉斯的双结合，即集平滑和边沿于一身的算子模型！注意这个模型跟前面的一个滤波器很相似，就是各向异性滤波器！只不过是各向异性滤波器是高斯一阶导函数，而LOG可以看做是二阶导函数！这两个模型来源最初都是因为求导导致模板对噪声干扰敏感性比较强！

1、拉普拉斯算子的出发点
在图像中，边缘可以看做是位于一阶导数较大的像素处，因此，我们可以求图像的一阶导数来确定图像的边缘，像sobel算子等一系列算子都是基于这个思想的。如下图a表示函数在边沿的时候关系，求导得b图，可知边沿可就是函数的极值点，对应二阶导数为0处，如图c的二阶导图。

                                 
                                                            (a)                                                                      (b)

                                                                                                    (c)
2、高斯-拉普拉斯算法
该算法就是直接对我们的高斯模型求二阶导数

高斯卷积函数定义为：

而原始图像f(x,y) 与高斯卷积定义为：

因为：

所以Laplacian of Gaussian(LOG)可以通过先对高斯函数进行偏导操作，然后进行卷积求解。公式表示为：

和

因此，我们可以LOG核函数定义为：

高斯二阶导如下图的绿色线，蓝色线是高斯一阶导数，红色则是高斯函数。

Laplacian of Gaussian计算可以利用高斯差分来近似，其中差分是由两个高斯滤波与不同变量的卷积结果逼近求得：

该函数逼近是因为发现高斯二阶导和原高斯函数对sigma参数求导之后函数模型的关系如上述的公式，然后约等于右边的导数表达式（严格的话需要加上极限的）！模型逼近如下：好处是可以提高算法的效率减少计算量

                                                                     

从两个平平滑算子的差分得出的是二阶边缘检测，反直观。近似计算可能如下图所示。图中一维空间，不同变量的两个高斯分布相减形成一个一维算子

注意最后计算的模板算子的权重和应该保证为1，不是1的可以进行归一化！确保在平塘区不会检测到边沿！
 

二、harris

Harris角点检测是Chris Harris和Mike Stephens在1988年提出的。主要用于运动图像的追踪。当时的普遍想法是利用边缘进行追踪，但是当相机或物体运动时你不知道朝哪个方向，相机的几何变换也是未知的，所以边缘匹配很难达到预期的效果。即使是当时最优秀的边缘检测算子Canny算子，它的边缘检测也依赖于阈值的选取。所以Harris等人放弃了匹配边缘，转而寻找一些特殊的点来匹配，这些点是边缘线段的连接点，它们表征了图像的结构，代表了图像局部的特征。
 

在做图像匹配时，常需要对两幅图像中的特征点进行匹配。为了保证匹配的准确性，所选择的特征必须有其独特性，角点可以作为一种不错的特征。

那么为什么角点有其独特性呢？角点往往是两条边缘的交点，它是两条边缘方向变换的一种表示，因此其两个方向的梯度变换通常都比较大并且容易检测到。

这里我们理解一下Harris Corner 一种角点检测的算法

角点检测基本原理：

人们通常通过在一个小的窗口区域内观察点的灰度值大小来识别角点，如果往任何方向移动窗口都会引起比较大的灰度变换那么往往这就是我们要找的角点。

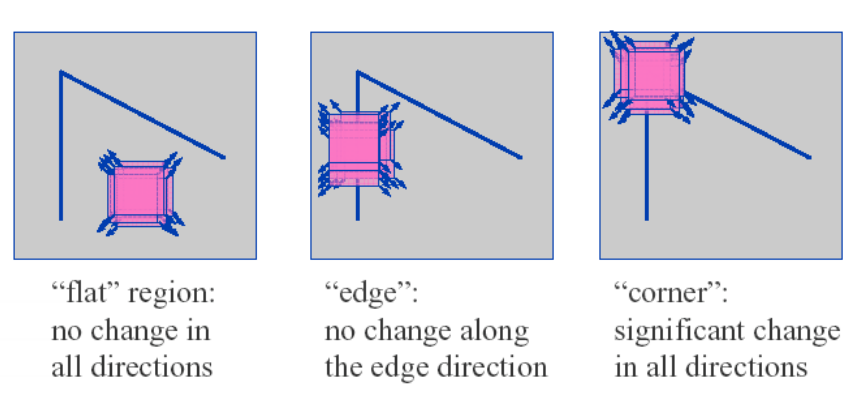
下面我们看一下Harris的数学公式，对于[x,y]平移[u,v]个单位后强度的变换有下式,I(x+u,y+v)是平移后的强度，I(x,y)是原图像像素。对于括号里面的值，如果是强度恒定的区域，那么它就接近于零，反之如果强度变化剧烈那么其值将非常大，所以我们期望E(u,v)很大。

 其中w是窗函数，它可以是加权函数，也可以是高斯函数

利用二维泰勒展开式我们有

 所以其中一阶可以近似为

于是我们可以给出Harris Corner的如下推导，其中Ix，Iy是x，y方向的Gradient模，乘以位移得到位移后的量

对于小的位移，我们可以用双线性插值方法近似：

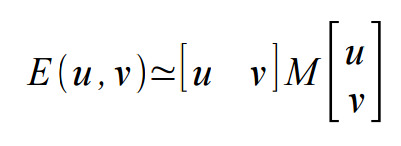
其中M为2*2矩阵如下

 在本质上我们可以把二次项看成一个椭圆函数，我们对M进行特征值分析有λ1，λ2

根据λ1，λ2的值我们可以把其分为三类：

1.λ1，λ2都很小且近似，E在所以方向接近于常数；

2.λ1>>λ2,或者λ2>>λ1, E将在某一方向上很大；

3.λ1，λ2都很大且近似，E将在所有方向上很大；

如图所示：

最后我们通过计算角点响应值R来判断其属于哪个区间

其中k一般为常数取在0.04-0.06间。

算法步骤：

1.计算图像x,y方向的梯度Ix，Iy

2.计算每个像素点的梯度平方

3.计算梯度在每个像素点的和

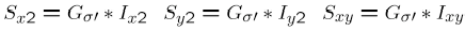
4.定义在每个像素点的矩阵H，也就是前面的M

5.计算每个像素的角点响应

6.设置阈值找出可能点并进行非极大值抑制

matlab程序

close all
clear all
 
I = imread('empire.jpg');
I = rgb2gray(I);
I = imresize(I,[500,300]);
imshow(I);
 
sigma = 1;
halfwid = sigma * 3;
 
[xx, yy] = meshgrid(-halfwid:halfwid, -halfwid:halfwid);
 
Gxy = exp(-(xx .^ 2 + yy .^ 2) / (2 * sigma ^ 2));
Gx = xx .* exp(-(xx .^ 2 + yy .^ 2) / (2 * sigma ^ 2));
Gy = yy .* exp(-(xx .^ 2 + yy .^ 2) / (2 * sigma ^ 2));
 
%%apply sobel in herizontal direction and vertical direction compute the
%%gradient
%fx = [-1 0 1;-1 0 1;-1 0 1];
%fy = [1 1 1;0 0 0;-1 -1 -1];
Ix = conv2(I,Gx,'same');
Iy = conv2(I,Gy,'same');
%%compute Ix2, Iy2,Ixy
Ix2 = Ix.*Ix;
Iy2 = Iy.*Iy;
Ixy = Ix.*Iy;
 
%%apply gaussian filter
h = fspecial('gaussian',[6,6],1);
Ix2 = conv2(Ix2,h,'same');
Iy2 = conv2(Iy2,h,'same');
Ixy = conv2(Ixy,h,'same');
height = size(I,1);
width = size(I,2);
result = zeros(height,width);
R = zeros(height,width);
Rmax = 0;
%% compute M matrix and corner response
for i = 1:height
    for j =1:width
        M = [Ix2(i,j) Ixy(i,j);Ixy(i,j) Iy(i,j)];
        R(i,j) = det(M) - 0.04*(trace(M)^2);
        if R(i,j)> Rmax
            Rmax = R(i,j);
        end
    end
end
%% compare whith threshold
count = 0;
for i = 2:height-1
    for j = 2:width-1
        if R(i,j) > 0.01*Rmax
            result(i,j) = 1;
            count = count +1;
        end
    end
end
 
%non-maxima suppression
result = imdilate(result, [1 1 1; 1 0 1; 1 1 1]);
 
[posc,posr] = find(result == 1);
imshow(I);
hold on;
plot(posr,posc,'r.');

三、SUSAN角点及边缘检测

SUSAN检测方法是一种基于窗口模板的检测方法，主要是通过在图像每个像素点位置处建立一个窗口，这个窗口是圆形的，这里为了得到各方向同性的响应，窗口内可以是常数权值或高斯权值，一般情况下，窗口半径为3.4个像素（即窗口内总有37个像素）。

这样的窗口模板被放置在每个像素的位置，确定点之间强度相似程度可以由下面的图来描述，这里的x轴是指像素点之间强度差别，y轴指的相似程度，为1就指完全相似。

                     

考虑为了运算简单，一般情况下使用a线（上图），最后统计所以同中心点相似的点数（即相似程度为1的点）相似点所在区域被称为USAN（Univalue Segment Assimilating Nucleus），而特征边缘或角点就是在这个点数值局部最小地方。图中的分界点（区分是否相似的像素差别）实际上反映了图像特征的最小对比程度，及被排除噪声的最大数目。

SUSAN边缘及角点检测没有用到图像像素的梯度（导数），因为这个原因，所以即使在噪声存在情况下，也能有好的表现。因为只要噪声足够的少，没有包含到所有相似像素的点，那么噪声就可以被排除。在计算时，单个值的集合统一消除了噪声的影响，所以SUSAN对于噪声具有较好的鲁棒性。

SUSAN是通过比较像素点邻域同其中心相似程度，所以也具有了光强变化不变性（因为像素点差别不会变化），及旋转不变性（旋转不会改变局部像素间的相似程度），及一定程度的尺度不变性（角点的角度在尺度放大并不会变化，这里的一定程度是指在尺度放大时，局部的曲度会慢慢平滑）。另外SUSAN使用的参数也非常的少，所以对于计算量及储存量要求低。

SUSAN方法被提出来，主要是为针对于边缘检测和角点检测的，然后其对于噪声较高的鲁棒性，也会用于在噪声消除中，被用于去选择最佳局部平滑邻域（相似程度的点最多的地方）。本文重点描述SUSAN方法用于边缘检测和角点检测的思路，并简要介绍下SUSAN方法是如何应用于噪声消除领域的。

 
一、SUSAN边缘检测

（1）边缘响应的计算
首先考虑到图像以每点像素为中心的圆形模板（半径为3.4个像素，模板内共有37个像素），对于其内的每个邻域点都作如下相似度衡量的计算（标准是上图的a线），这里的r是领域像素距离中心的长度，而r0是中心位置，t指相似度分界值（其决定了特征同背景的最小区别程度，及最大可被排除的噪声数）。

当然我们也可以用平滑的线来从代替这种直接的分割方式（如下图b线），这样可以获得更稳定而敏感的结果，虽然计算复杂但是可以通过查找表来获得较快的速度。公式如下：

并计算总共的相似程度：

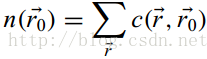
接下来，将n同一个固定的阈值g比较（一般设置为最大同中心相似点数nmax的0.75倍左右），初始的边缘响应可以用下面等式计算：

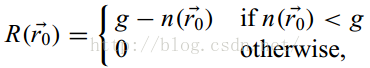
这里g是为了排除噪声的影响，而当n小于这个阈值时，才能被考虑其的边缘是否是边缘，n越小，其边缘响应就越大。如果一个阶跃边缘被考虑，如果这个点在边缘上，那么其USAN的值应当是小于或等于0.5倍的最大值，而对于曲线边缘来说，这个值应该会更少（因为曲度会更小，所以在窗口内，曲线内的区域会更小），所以g的加入不会影响原来的边缘检测的结果的（即所得的边缘响应R是不会为0的）。

（2）边缘方向的计算
为什么要计算边缘方向呢？首先，非极大值抑制需要找到边缘方向（这个之后再解释），另外确定子像素级精度也需要找到边缘方向（这个好理解），最后，一些应用可以会用到边缘方向（也包括位置及长度），一个像素若其边缘长度不会0，那么便有边缘方向，边缘一般有两种情况：

一种是标准的边缘点（如同中的a和b，其刚好位于边缘的一边或另一边），而c是另一种情况，其刚好位于左右两边的过渡带间，而过渡带的强度恰好为左右像素强度的一半。这里还引入了一个概念，USAN的引力中心（USAN区域即图像模板内的白色区域，就是同中心相似的区域），其可以由下式计算：

其中a和b情况可以被视一种像素间边缘，引力中心同模板中心的向量恰好垂直于局部边缘方向，我们可以通过这种方式来找到其边缘方向。

而上图c的情况就完全不一样了，其引力中心同模板中心恰好在一点上（这被视为一种像素内边缘），此时边缘的方向就要找到USAN区域内最长的对称轴方向，这个可以通过如下公式来获得：

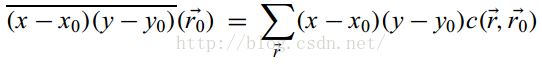
前两项的比值可以用于确定边缘的方向（度数），而后一项的符号用于确定一个倾斜边缘其梯度的符号（往那边倾斜）。
接下来的问题就是如何自动决定每点是属于以上哪种的边缘，首先如果USAN区域（像素数）比模板直径（像素数）要小，那么这应该是像素内边缘（如c）。如果要大的话，然后又找到USAN的引力中心，那么这应该是像素间边缘情况（如a和b）。如果引力中心同模板中心的距离小于1个像素的话，此时用于像素内边缘情况（如c）来计算更为精确。

（3）非极大值抑制
（4）子像素精度

对于每一个边缘点，首先找到边缘方向，然后在边缘垂直方向上减少边缘宽度，之后剩下的边缘点做3点二次曲线拟合，而曲线的转折点（一般情况下同最初边缘点的距离应当少于半个像素）被视为边缘的精确位置。

（5）检测位置并不依赖于窗口大小

即窗口模板增大，不会改变检测的边缘的位置，即SUSAN具有尺度不变性，另外其对于视点改变后的图像检测重复率也非常高，因为视点变化不会影响其角点是否存在。
 
二、SUSAN角点检测方法

角点检测方法同其边缘检测方法非常类似，其使用相同的方法来计算每个像素点的同圆形窗口内的相似程度n，然后n也是同一个权值g来比较，不过这里的g只是控制噪声存在数目，而需要考虑边缘，所以g的值为nmax的一半就可以了。

在特征检测方法里，我们一般需要至少一个阈值来区分特征同非特征，而这个阈值的选择将极大影响了最终特征提取的结果。一般情况下，这里有两种类型的阈值：一个衡量质量，一个衡量数量。SUSAN方法里的t和g恰好分别符合这两种情况，g控制角点检测的质量，如果g越小，那么我们得到的角点就更尖锐，而t则控制角点数目，如果t越小，那么我们检测的角点数目就越小，然后t却不会影响最终角点质量。（这段是题外话了>_<）

在计算角响应度后，而在非极大值抑制之前，我们可以排除一些在边缘或噪声位置的误检测角点，比如一条倾斜率比较小的直线，因为边缘线至少要一个像素宽度，所以会在直线上形成不连续断裂，这些断裂的位置可能会形成被误检的角点（如上图的c）。

（1）排除误检的角点
首先找到USAN的引力中心，然后计算引力中心同模板中心的距离，当USAN恰好能指示一个正确角点时，其引力中心同模板中心将不会靠得太近，而如果是条细线的话，引力中心同模板中心将会很近（如上图a和b所示）。另外的操作就是要加强USAN的邻近连续性，在真实图像里，非常容易出现小的噪声点，而这些噪声点可能分布于USAN内。所以对于模板内所有的像素，如果其是位于引力中心同模板中心所连的直线上，那么都应该视为USAN的一部分。

（2）非极大值抑制
SUSAN角点检测方法同基于导数检测方法一个非常大的优势在于，其不会在靠近中心相邻的区域不会与中心区域的角响应很难区分，所以局部的非极大值抑制中需要简单地选择局部的最大值就可以了。
 
三、SUSAN噪声滤波方法

SUSAN噪声滤波方法主要是通过仅平滑那些同中心像素相似的区域（即USAN），而由此保留图像的结构信息。而USAN的平滑主要就是找到其中所以像素的平均值，而不会对其相邻的不相关区域进行操作。
不过在区分相似度的公式上，却没有用到原来的公式，而是如下：

滤波器的最终公式为：

参考文献
SUSAN—ANew Approach to Low Level Image Processin

Harris Corner Detector 公式推导以及具体含义_Focusing on your own Mind :) －> 站在巨人的肩膀上-CSDN博客

LOG高斯-拉普拉斯算子_Touch_Dream的博客-CSDN博客_高斯差分算子