读书笔记: Cartesian Impedance Control of Redundant and Flexible-Joint Robots, Section 2

Cartesian Impedance Control of Redundant and Flexible-Joint Robots 读书笔记

Section 2 柔性关节机器人建模

只考虑开链机器人的情况，机器人柔性分两部分：分布参数弹性是各连杆形变导致的柔性，集中参数部分是由齿轮导致的弹性。本书只讨论后者。

2.1 运动学

本书采用的旋量是$v$在上,$\omega$在下，既与《A Mathematical Introduction to Robotic Manipulation》保持一致。
$$V^b=\left(\begin{array}{c}{}_b{v}_{sb}\\ {}_b{\omega }_{sb}\end{array}\right)$$
${}_b{\omega }_{sb}$的左下标$b$表示该向量表达在$B$系中，右下标$sb$表示这是${\omega }_{sb}$
除此之外运动学部分没有啥需要特别注意的。

2.2 柔性关节机器人动力学模型

动力学模型有两个：完整模型和简化模型。简化模型假设转子的动能仅有其旋转产生。

2.2.1 Complete Model的假设

• 假设1：电机转子是旋转对称的刚体，并且对称中心与运动的旋转中心一直
• 假设2：电路部分的动态特性(内环电流环)足够快，相较于机械特性而言可以忽略

这两条假设是说，电机可以看成一个理想的转矩源，$i$关节电机的转矩为${\tau }_{motor,i}$
考虑传动比$N_i$后，
$${\tau }_{m,i}=N_i{\tau }_{motor,i}{\theta }_i=\frac{1}{N_i}{\theta }_{motor,i}$$

• 假设3：齿轮的弹性可用线性弹簧表示，弹簧位于转子与下一个link之间的
  
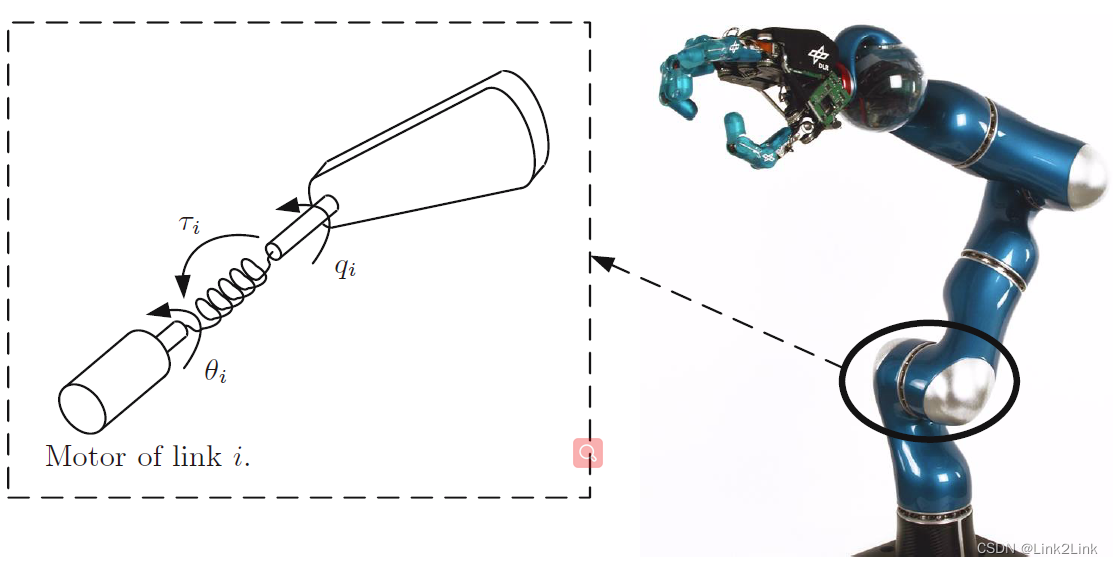
  $q_i$是关节角，及下一个link与本link之间的夹角，${\theta }_i$是经过传动比折算之后的电机角。因此弹簧力是$${\tau }_i=K_i({\theta }_i-q_i)$$这个关节的弹性势能是$$V_{k,i}=\frac{1}{2}{K}_i({\theta }_i-q_i{)}^2$$结合实际，${\theta }_i$是由在电机轴上测出来的角(一般是增量编码器)，$q_i$是输出端测出来的角度(一般是绝对值编码器)。

2.2.2 Complete Model推导

对于有$n$个关节的开链机器人
坐标系这么建

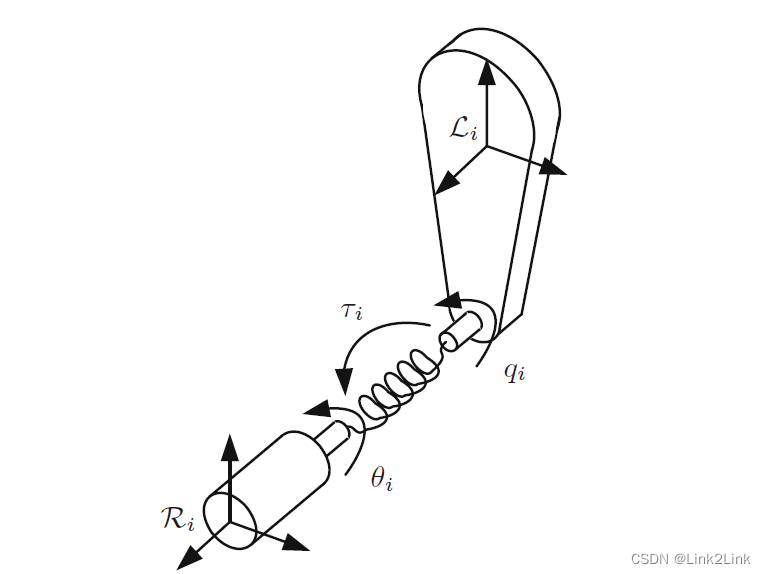
对关节$i$，$L_i$放在与之相连的Link_i的质心，$R_i$放在前一个link的转子处，z轴与旋转方向一致。
因此，Links的动能是
$$T_l\left(q,\dot{q}\right)=\frac{1}{2}\sum _{i=1}^n{\left(V_{l,i}^b\right)}^T{\mathcal{M}}_{l,i}{V}_{l,i}^b$$
构造惯性矩阵
$$M_l\left(q\right)=\sum _{i=1}^n{J}_{l,i}^b{\left(q\right)}^T{\mathcal{M}}_{l,i}{J}_{l,i}^b\left(q\right)$$
于是有
$$T_l\left(q,\dot{q}\right)=\frac{1}{2}{\dot{q}}^T{M}_l\left(q\right)\dot{q}$$

然后计算转子动能:
电机的定子固连在前一级link上，转子在相对于定子旋转，旋转角度是${\theta }_i$，因此计算转子的6维速度旋量时需要在$R_i$对应的虚度旋量上进行叠加，有
$$V_{r,i}^b=J_{r,i}^b\left(q\right)\dot{q}+\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\end{array}\right){\dot{\theta }}_i$$
这里需要注意的是这个计算是在$R_i$系里进行的，而不是$L_i$系，所以转子动能是
$$T_r\left(q,\dot{q},\dot{\theta }\right)=\frac{1}{2}\sum _{i=1}^n{\left(V_{r,i}^b\right)}^T{\mathcal{M}}_{r,i}{V}_{r,i}^b$$
犹豫对称性假设，在$R_i$系表达的惯性张量应为 I r , i = d i a g { A i , B i , C i } I_{r,i}=diag\{A_i,B_i,C_i\} Ir,i​=diag{Ai​,Bi​,Ci​}，整理后有

$$T_r\left(q,\dot{q},\dot{\theta }\right)=\frac{1}{2}{\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)}^T\left(\begin{array}{cc}{M}_r\left(q\right)& S\left(q\right)\\ S{\left(q\right)}^T& B\end{array}\right)\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)$$
其中,$$M_r\left(q\right)=\sum _{i=1}^n{J}_{r,i}^b{\left(q\right)}^T{\mathcal{M}}_{r,i}{J}_{r,i}^b\left(q\right)$$
$$S\left(q\right)=\left[s_1\left(q\right)...s_2\left(q\right)\right]$$
$$s_i\left(q\right)=J_{r,i}^b{\left(q\right)}^T\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ B_i\end{array}\right)$$

$$B=\mathrm{diag}\left(B_i\right)$$
两部分动能之和是系统动能
$$T\left(q,\dot{q},\dot{\theta }\right)=\frac{1}{2}{\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)}^T\left[\begin{array}{cc}{M}_l\left(q\right)+M_r\left(q\right)& S\left(q\right)\\ S{\left(q\right)}^T& B\end{array}\right]\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)$$

再计算势能部分，各个关节的弹性势能有
$$V_k\left(q,\theta \right)=\frac{1}{2}{\left(\theta -q\right)}^{T}K\left(\theta -q\right)$$
$K=diag(K_i)$是个对角矩阵
对重力势能部分，设$m_{l,i}$是link_i的质量，$m_{r,i}$是转子的质量。$e_g$是重力的方向向量，$g$是重力加速度，于是有
$$V_g\left(q\right)=-g{e}_g^T\sum _{i=1}^n\left(m_{l,i}{p}_{sl,i}\left(q\right)+m_{r,i}{p}_{sr,i}\left(q\right)\right)$$
所以i，势能是
$$V_{pot}\left(q,\theta \right)=V_g\left(q\right)+\frac{1}{2}{\left(\theta -q\right)}^{T}K\left(\theta -q\right)$$

把$q$和$\theta$摞起来构成广义坐标
$$\hat{q}=\left(\begin{array}{c}q\\ \theta \end{array}\right)$$
拉格朗日函数
$$L\left(\hat{q},\dot{\hat{q}}\right)=T-V_{pot}$$
带入拉格朗日方程
$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\hat{q}}}\right)-\frac{\partial L}{\partial \hat{q}}=Q$$
得到

$$H\left(q\right)\left(\begin{array}{c}\ddot{q}\\ \ddot{\theta }\end{array}\right)+\Gamma \left(q,\dot{q}\right)\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)+\left(\begin{array}{c}g\left(q\right)-K\left(\theta -q\right)\\ K\left(\theta -q\right)\end{array}\right)=\left(\begin{array}{c}{\tau }_{ext}\\ {\tau }_m\end{array}\right)$$
其中$H(q)$是完整的惯性矩阵，$H(q)\ddot{\hat{q}}$是加速度产生的惯性力$$H\left(q\right)=\left[\begin{array}{cc}{M}_l\left(q\right)+M_r\left(q\right)& S\left(q\right)\\ S{\left(q\right)}^T& B\end{array}\right]$$
$g(q)是重力矩$
$$g\left(q\right)={\left(\frac{\partial V_g\left(q\right)}{\partial q}\right)}^T$$

$\Gamma \left(q,\dot{q}\right)\dot{\hat{q}}$包含了科里奥利力和离心力，$\Gamma \left(q,\dot{q}\right)$比较复杂，表达式是
$$\begin{gathered} {\Gamma }_{ij}\left(q,\dot{q}\right)=\sum _{k=1}^{2n}{\Gamma }_{ijk}\left(q\right){\dot{\hat{q}}}_k \\ {\Gamma }_{ijk}\left(q\right)=\frac{1}{2}\left(\frac{\partial H_{ij}\left(q\right)}{\partial {\hat{q}}_k}+\frac{\partial H_{ik}\left(q\right)}{\partial {\hat{q}}_j}-\frac{\partial H_{kj}\left(q\right)}{\partial {\hat{q}}_i}\right) \end{gathered}$$
上方红色的方程就是所谓的柔性关节机器人的完整动力学模型(complete model of a flexible joint robot)。如果把其中$S(q)$部分忽略，就是接下来的简化动力学模型。

2.2.3 Reduced Model

简化模型的假设：

• 假设4 ： 电机转子的动能只包含其旋转产生的转动动能，而忽略因其他关节运动所产生的的动能。换言之，认为电机转子没有质量只有转动惯量。这个假设对应的物理事实是在减速比作用下，电机转子的旋转速度一般比较高，因此转动动能占主导地位，另外很多机器人设计通过线驱把电机给后置到基座上，

在这个假设下，转子动能简化为
$$T_r\left(q,\dot{q},\dot{\theta }\right)=\frac{1}{2}{\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)}^T\left(\begin{array}{cc}{\bar{M}}_r\left(q\right)& 0\\ 0& B\end{array}\right)\left(\begin{array}{c}\dot{q}\\ \dot{\theta }\end{array}\right)$$
${\bar{M}}_r\left(q\right)$部分也发生变化，简化后为
$$\begin{gathered} {\bar{M}}_r\left(q\right)=\sum _{i=1}^n{m}_{r,i}{\bar{J}}_{r,i}^b{\left(q\right)}^T{\bar{J}}_{r,i}^b\left(q\right) \\ {\bar{J}}_{r,i}^b\left(q\right)=\left[\begin{array}{cc}{I}_{3\times 3}& 0_{3\times 3}\end{array}\right]J_{r,i}^b\left(q\right) \end{gathered}$$

简化之后的动力学模型为

$$\begin{gathered} M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+g\left(q\right)=K\left(\theta -q\right)+{\tau }_{ext} \\ B\ddot{\theta }+K\left(\theta -q\right)={\tau }_m \end{gathered}$$
其中$M(q)=M_l(q)+{\bar{M}}_r(q)$，$C\left(q,\dot{q}\right)$是与$M$对应的科里奥利矩阵。

2.2.4 动力学模型的性质

• 欠驱动：模型状态变量数量是$2n$但是只有$n$个控制输入(电机力矩)。
• 微分平坦：完整模型和简化模型都是微分平坦的，简化模型可以通过静态状态反馈来线性化参见[经典论文Spo87b]，完整模型可以通过动态状态反馈线性化[经典论文DLL98]
• 惯性矩阵$M(q)$是对称正定
• $\dot{M}-2C$矩阵反对称

对包含平移关节的机器人，$Q^p$是考虑各个关节限位之后的位形空间
Q p = { q ∈ Q ∣ q i , m i n ≤ q i ≤ q i , m a x } Q^p=\{q\in Q | q_{i,min} \le q_i \le q_{i,max}\} Qp={q∈Q∣qi,min​≤qi​≤qi,max​}
对于后续的阻抗控制设计还有以下重要性质

• 在$Q^p$内，${\lambda }_i(M(q))$有界 $$0<{\lambda }_{m,M}\le {\lambda }_i(M(q))\le {\lambda }_{M,M}<\infty$$
• 重力矩$g\left(q\right)={\left(\frac{\partial V_g\left(q\right)}{\partial q}\right)}^T$，对各种矩阵范数都存在一个$\alpha >0$使得$$||\frac{\partial g\left(q\right)}{\partial q}||<\alpha$$

2.2.5 摩擦力

以上动力学模型都没有包含摩擦力，如果只考虑粘滞摩擦，则不会会影响模型的反馈线性化，这本书只考虑粘滞摩擦的情况。在实际中使用应该进行摩擦补偿。