读书笔记: Cartesian Impedance Control of Redundant and Flexible-Joint Robots , Section 3

Section 3 刚性机器人的阻抗控制

本章先介绍的是刚性机器人的阻抗控制，之前建模中的$K(\theta -q)$直接替换成$\tau$即可得到动力学方程。

3.1 经典阻抗控制

因为没有了柔性部分，模型里的第二行也就没了，模型变成了
$$M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+g\left(q\right)=\tau +{\tau }_{ext}$$

3.1.1 任务描述

阻抗控制的目标是在机器人和外界环境之间构建特定的动态关系。先假设已经选择好了表达末端位姿的方法，比如笛卡尔坐标$\mathbf{x}=(x,y,z,\alpha ,\beta ,\gamma )$，先不关心具体怎么选。根据运动学就可以得到$x=f(q)$。本章先不讨论冗余自由度的情况，因此有$m=n$，先计算$x$的导数
$$\begin{gathered} \dot{x}=\mathbf{J}\left(\mathbf{q}\right)\dot{q} \\ \ddot{x}=\mathbf{J}\left(\mathbf{q}\right)\ddot{q}+\dot{J}\left(\mathbf{q}\right)\dot{q} \end{gathered}$$
考虑$x=f(q)$这个函数，对旋转关节来说$x$是$q$的三角函数,对平移关节$x$是$q$的仿射函数，因此整体上$x$是$q$的三角函数级联仿射函数。因此其雅克比矩阵的奇异值是有界的
$${\sigma }_{M,J}=\underset{q\in Q^p}{\sup }{\sigma }_{\max }\left(J\left(q\right)\right)<\infty$$
而在选择的工作工作空间内也要求没有奇异点因此,雅克比矩阵也有最小值
$$0<{\sigma }_{m,J}=\underset{q\in Q^p}{\inf }{\sigma }_{\min }\left(J\left(q\right)\right)$$
函数$x=f(q)$将关节空间$Q^p$映射到笛卡尔空间，假设在${\bar{Q}}^p$上是一个一一映射，其相应的象为${\bar{Q}}_c^p$。在${\bar{Q}}_c^p$内$x$可视作机器人的广义坐标。
同样，负载转矩${\tau }_{ext}$也需要被表达在笛卡尔空间
$${\tau }_{ext}=J(q{)}^T{F}_{ext}$$
阻抗控制的目标是让$x$与给定点$x_d$时间的误差$\tilde{x}=x-x_d$体现出阻抗特性
$${\Lambda }_d\ddot{\tilde{x}}+D_d\dot{\tilde{x}}+K_d\tilde{x}=F_{ext}$$
这是一个6维表达式，其中有三个是姿态相关，三个是位置相关。

3.1.2 任务空间的机器人模型

为了把模型映射到任务空空间中，只需带入$\ddot{q}=J{\left(q\right)}^{-1}\left(\ddot{x}-\dot{J}\left(q\right)\right)\dot{q}$和${\tau }_{ext}=J{\left(q\right)}^T{F}_{ext}$，于是有
$$\begin{gathered} J{\left(q\right)}^{-T}M\left(q\right)J{\left(q\right)}^{-1}\ddot{x}+J{\left(q\right)}^{-T}C\left(q,\dot{q}\right)J{\left(q\right)}^{-1}\dot{x}-J{\left(q\right)}^{-T}M\left(q\right)J{\left(q\right)}^{-1}\dot{J}\left(q\right)J{\left(q\right)}^{-1}\dot{x} \\ +J{\left(q\right)}^{-T}g\left(q\right)=J{\left(q\right)}^{-T}\tau +F_{ext} \end{gathered}$$
这个重写为
$$\Lambda \left(x\right)\ddot{x}+\mu \left(x,\dot{x}\right)\dot{x}+F_g\left(x\right)=F_{\tau }+F_{ext}$$
其中
$$\begin{gathered} \Lambda \left(x\right)=J{\left(q\right)}^{-T}M\left(q\right)J{\left(q\right)}^{-1} \\ \mu \left(x,\dot{x}\right)=J{\left(q\right)}^{-T}\left(C\left(q,\dot{q}\right)-J{\left(q\right)}^{-T}M\left(q\right)J{\left(q\right)}^{-1}\dot{J}\left(q\right)\right)J{\left(q\right)}^{-1} \\ {F}_g\left(x\right)=J{\left(q\right)}^{-T}g\left(q\right) \\ {F}_{\tau }=J{\left(q\right)}^{-T}\tau \end{gathered}$$

对这个方程有以下性质:

• $\Lambda \left(x\right)$对称正定
• $\dot{\Lambda }\left(x\right)-2\mu \left(x,\dot{x}\right)$是反对称矩阵
  这两个性质保持与关节空间中相同，一个基本认识是在人物空间中，只是换了个坐标系，动力学系统本身的特性其实没有变
  ，也就是说可以直接用克氏符(Christoffel symbol)来计算$\mu (x,\dot{x})$
• 类似的，$\lambda (\Lambda \left(x\right))$是有界的

3.1.3 经典阻抗控制

经典的阻抗控制的表达式为
$$F_{\tau }=F_g\left(x\right)+\Lambda \left(x\right){\ddot{x}}_d+\mu \left(x,\dot{x}\right)\dot{x}-\Lambda \left(x\right){\Lambda }_d^{-1}\left(K_d\tilde{x}+D_d\dot{\tilde{x}}\right)+\left(\Lambda \left(x\right){\Lambda }_d^{-1}-I\right)F_{ext}$$
产生此空间力的关节转矩是
$$\begin{array}{rl}\tau & =J{\left(q\right)}^T{F}_{\tau }\\ & =g\left(q\right)+J{\left(q\right)}^T\left(\Lambda \left(x\right){\ddot{x}}_d+\mu \left(x,\dot{x}\right)\dot{x}\right)-J{\left(q\right)}^T\Lambda \left(x\right){\Lambda }_d^{-1}\left(K_d\tilde{x}+D_d\dot{\tilde{x}}\right)+J{\left(q\right)}^T\left(\Lambda \left(x\right){\Lambda }_d^{-1}-I\right)F_{ext}\end{array}$$

3.2 消除外力项

只需调配${\Lambda }_d^{}$使得
$${\Lambda }_d=\Lambda \left(x\right)$$
既可消除控制中的$F_{ext}$项，但是相应的闭环动力学也会变成
$$\Lambda \left(x\right)\ddot{\tilde{x}}+\left(\mu \left(x.\dot{x}\right)+D_d\right)\dot{\tilde{x}}+K_d\tilde{x}=F_{ext}$$
此时，控制率简化为
$$\tau =g\left(q\right)+J{\left(q\right)}^T\left(\Lambda \left(x\right){\ddot{x}}_d+\mu \left(x,\dot{x}\right)\dot{x}-K_d\tilde{x}-D_d\dot{\tilde{x}}\right)$$
称为"柔顺控制"或“PD+控制”。

3.3 阻尼矩阵

在配置${\Lambda }_d=\Lambda \left(x\right)$之后，$D_d$的设计变得不直观了，根据术中证明，只要$D_d(x)$是一个关于$x$的正定矩阵，控制器就是渐进稳定的。本书给出了其中一种方法。

• 引理3.6(广义特征值分解)：给定一个对称正定矩阵$A$和一个对称矩阵$B$，能找到一个非奇异矩阵$Q$和一个对角矩阵$B_0$，使得$Q^{T}Q=A$和$Q^T{B}_{0}Q=B$

对系统做quasi-static分析，并且忽略$\mu$这一项，既对以下系统
$$\Lambda \left(x_0\right)\ddot{\tilde{x}}+D_d\left(x_0\right)\dot{\tilde{x}}+K_d\tilde{x}=F_{ext}$$
将$\Lambda \left(x_0\right)$视作$A$，$K_d$视作$B$，于是有
$$Q{\left(x_0\right)}^{T}Q\left(x_0\right)\ddot{\tilde{x}}+D_d\left(x_0\right)\dot{\tilde{x}}+Q{\left(x_0\right)}^T{B}_0\left(x_0\right)Q\left(x_0\right)\tilde{x}=F_{ext}$$
${\lambda }_i$是$B_0$的第$i$个对角元，也就是$K_d$相对于$\Lambda (x_0)$的第$i$个广义特征值。则$D_d(x_0)$矩阵可以选为
$$D_d\left(x_0\right)=2Q{\left(x_0\right)}^T\mathrm{diag}\left({\xi }_i\sqrt{{\lambda }_i}\right)Q\left(x_0\right)$$
其中${\xi }_i$是一个阻尼系数在$[0,1]$
在这个$D_d$的选择下，系统和以写成
$$\ddot{z}+2\mathrm{diag}\left({\xi }_i\sqrt{{\lambda }_i}\right)\dot{z}+\mathrm{diag}\left(\sqrt{{\lambda }_i}\right)z=Q{\left(x_0\right)}^{-T}{F}_{ext}$$
这种设计方法得到的$D_d$不影响稳定性，既只保证了$D_d(x_0)$正定

3.4 处理奇异性

之前都假设$J(q)$非奇异，在一般情况下，有两种奇异性：representation singularities 和 kinematic singularties，前者是因为坐标系选取问题导致的奇异，如欧拉角，可通过选取合理的坐标域或者使用冗余表达如四元数来避免； 后者是因为机器人构型导致的运动学奇异，这个是在机构设计确定之后就是无法避免的。

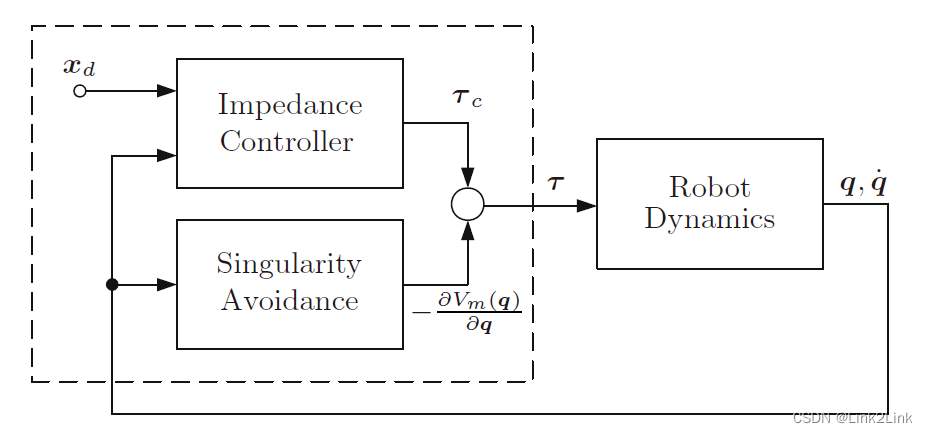
利用叠加原理，在原本阻抗控制的基础上叠加一个控制用来回避奇异点。
定义一个所谓的距离
$$m_{kin}\left(q\right)=\sqrt{\det \left(J\left(q\right)J{\left(q\right)}^T\right)}$$
用来回避奇异点的势能可以被选择为
$$V_m\left(q\right)=\{\begin{array}{cc}{k}_s{\left(m_{kin}\left(q\right)-m_0\right)}^2& m_{kin}\left(q\right)\le m_0\\ 0& m_{kin}\left(q\right)>m_0\end{array}$$
$k_0$是一个正的增益，$m_0$定义了一个奇异点附近的邻域，仅在这个邻域内才附加SingularityAvoidance的控制。
另${\tau }_c$表示前文的阻抗控制，则带奇异点回避之后的新控制为
$$\tau ={\tau }_c-\frac{\partial V_m\left(q\right)}{\partial q}$$

3.5 姿态表示方法与刚度矩阵

将坐标$x\in {\mathbb{R}}^6$分成两组，$x_t\in {\mathbb{R}}^3$表示位置，一般采用笛卡尔坐标系；$x_r\in {\mathbb{R}}^3$表示姿态，采用不同的表示方法将会有不一样的效果。将坐标分成两组之后，刚度矩阵也有对应的分割
$$K_d=\left[\begin{array}{cc}{K}_t& K_c\\ K_c^T& K_r\end{array}\right]$$
末端的当前位姿矩阵是$h_{st}(q)$,以及一个期望的时变位姿$h_{sd}(t)$，有$$h_{dt}\left(q,t\right)=h_{sd}^{-1}\left(t\right)h_{st}\left(q\right)=\left[\begin{array}{cc}{R}_{dt}\left(q,t\right)& {}_d{p}_{dt}\left(q,t\right)\\ 0& 1\end{array}\right]$$

3.5.1 平移刚度

向量${}_d{p}_{dt}\left(q,t\right)$由期望的位置$p_d$指向当前位置$p_t$，表达在$d$系中，将其表达在s系中有
$$p_{dt}\left(q,t\right)=R_{sd}{\left(t\right)}_s{p}_{dt}\left(q,t\right)=p_{st}\left(q\right)-p_{sd}\left(t\right)$$
刚度矩阵$K_t$的三个特征向量，对应着三个刚度方向(表达在s系中)。
一些应用希望将刚度定义在$d$系或$t$系中，就需要使用相应系中的坐标。例如${}_d{p}_{dt}$被用作平移误差${\tilde{x}}_t$,相应的刚度就表达在$d$系中。

3.5.2 旋转刚度

相比于平移刚度的直观性，旋转刚度比较复杂，我们都知道SO3与R3不同胚，所以不存在一个最小的全局坐标表达。更多的关于姿态表示方法的讨论参见书中参考资料。这里只讨论欧拉角

考虑欧拉角${\varphi }_{st}\left(q\right)=\varphi \left(R_{st}\left(q\right)\right)$，一个方法是直接将欧拉角的差作为姿态误差${\varphi }_{dt}^{\ast }\left(q,t\right)={\varphi }_{st}\left(q\right)-{\varphi }_{sd}\left(t\right)$，但这种方法存在一个问题，这两组欧拉角任何一个出现奇异的时候，这个误差计算都是奇异的。一个更好的方法是用位姿误差$h_{td}$来算欧拉角误差${}_t{\varphi }_{td}\left(q,t\right)=\varphi \left(R_{td}\left(q,t\right)\right)$,此方法就奇异性而言鲁棒性更佳。当然，也可表达在s系中。

3.5.3 对闭环系统的影响

前两节说明了不能直接用两个坐标之间的差做笛卡尔误差，这里讨论如何更改之前的公式使其适合于前两节的情况。计算误差向量的导数
$$\begin{gathered} \dot{\tilde{x}}=\frac{\partial \tilde{x}\left(q,t\right)}{\partial q}\dot{q}+\frac{\partial \tilde{x}\left(q,t\right)}{\partial t} \\ \ddot{\tilde{x}}=\frac{\partial \tilde{x}\left(q,t\right)}{\partial q}\ddot{q}+\frac{d}{dt}\left(\frac{\partial \tilde{x}\left(q,t\right)}{\partial q}\right)\dot{q}+\frac{d}{dt}\frac{\partial \tilde{x}\left(q,t\right)}{\partial t} \end{gathered}$$
另
$$\begin{gathered} \frac{\partial \tilde{x}\left(q,t\right)}{\partial q}=J_x\left(q,t\right) \\ \frac{\partial \tilde{x}\left(q,t\right)}{\partial t}=-v_t\left(q,t\right) \end{gathered}$$
做与3.1.2相同的推导可以得到
$$\begin{gathered} \Lambda \left(q,t\right)\left(\ddot{\tilde{x}}+v_t\left(q,t\right)\right)+\mu \left(q,\dot{q},t\right)\left(\dot{\tilde{x}}+v_t\left(q,t\right)\right)+J_x{\left(q,t\right)}^{-T}g\left(q\right)=J_x{\left(q,t\right)}^{-T}\left(\tau +{\tau }_{ext}\right) \\ \Lambda \left(q,t\right)=J_x{\left(q,t\right)}^{-T}M\left(q\right)J_x{\left(q,t\right)}^{-1} \\ \mu \left(q,\dot{q},t\right)=J_x{\left(q,t\right)}^{-T}\left(C\left(q,\dot{q}\right)-M\left(q\right)J_x{\left(q,t\right)}^{-1}{\dot{J}}_x\left(q,t\right)\right)J_x{\left(q,t\right)}^{-1} \end{gathered}$$
相对于之间的公式，只是做了如下代换
$$\begin{gathered} J\left(q\right)\to J_x\left(q,t\right) \\ {\dot{x}}_d\to -v_t\left(q,t\right) \\ {\ddot{x}}_d\to -{\dot{v}}_t\left(q,t\right) \end{gathered}$$