读书笔记: Cartesian Impedance Control of Redundant and Flexible-Joint Robots , Section 4

Section 4 零空间控制

前面讨论的都是6自由度机器人，机器人自由度大于6时，就需要考虑冗余的问题。
正向运动学映射$f:Q\to {\mathbb{R}}^m$将位形空间映射为任务空间，其相应的分析雅克比为$J(q)=\frac{\partial f(q)}{\partial q}\in {\mathbb{R}}^{m\times n}$
$$\begin{gathered} x=f(q) \\ \dot{x}=J(q)\dot{q} \end{gathered}$$
在冗余的情况下$m<n$，因此末端位姿不能完全反映机器人的位形。

本章只讨论非奇异情况，既雅克比矩阵满秩$rank(J(q))=m$,
同样，假设已经有了动力学模型
$$M(q)\ddot{q}+C(q,\dot{q})\dot{q}+g(q)=\tau +{\tau }_{ext}$$
处理冗余的方法是对任务坐标进行扩充，既添加$r=n-m$个辅助变量或者叫零空间坐标。本章主要谈论寻找合适的坐标和动力学的零空间分解。

4.1 计算零空间的基

本节介绍如何计算雅克比$J(q)$的Nullspace的基矩阵$Z(q)$。

4.1.1 General Case

只考虑满秩的情况，通过重新排列每一列，$J(q)$可以写成
$$J\left(q\right)=\left[\begin{array}{cc}{J}_m\left(q\right)& J_r\left(q\right)\end{array}\right]$$
使得$J_m(q)$是可逆的。

另零空间基矩阵也做相同分割$$Z\left(q\right)=\left[\begin{array}{cc}{Z}_m\left(q\right)& Z_r\left(q\right)\end{array}\right]$$
其中$Z_m$和$Z_r$都是待定矩阵使得$J(q)Z(q{)}^T=0$，并且Z(q)行满秩。用上面的符号，这个等式可写成
$$J_m\left(q\right)Z_m{\left(q\right)}^T+J_r\left(q\right)Z_r{\left(q\right)}^T=0$$
一个可行解是
$$\begin{gathered} Z_m{\left(q\right)}^T=-J_m{\left(q\right)}^{-1}{J}_r\left(q\right) \\ {Z}_r\left(q\right)=I \end{gathered}$$
既，零空间基矩阵为$$Z\left(q\right)=\left[\begin{array}{cc}-J_m{\left(q\right)}^{-1}{J}_r\left(q\right)& I\end{array}\right]$$

4.1.2 1D零空间情况

在一维零空间的情况下可以避免计算$J_m(q)$的逆。在此情况下零空间的基是一个向量$z(q)=[z_1(q),......,z_n(q)]$，考虑这个矩阵
$$J_z\left(q\right)=\left(\begin{array}{c}J\left(q\right)\\ z\left(q\right)\end{array}\right)$$
只需找到一个$z(q)$使得矩阵$J_z(q)$可逆。
推导不困难，直接写结果
$$z_i\left(q\right)={\left(-1\right)}^{n+i}\det \left(J_i\left(q\right)\right)$$
$J_i\left(q\right)\in {\mathbb{R}}^{n\times n}$是矩阵$J(q)$去掉第$i$列产生。

4.2 基于投影方法

之前提到的阻抗控制表达式是
$$\begin{gathered} {\tau }_c=g\left(q\right)+J{\left(q\right)}^T{F}_{imp} \\ {F}_{imp}=\Lambda \left(x\right){\ddot{x}}_d+\mu \left(x,\dot{x}\right){\dot{x}}_d-K_d\tilde{x}-D_d\dot{\tilde{x}} \end{gathered}$$
根据叠加原理，添加零空间控制之后可直接写为
$$\tau ={\tau }_c+{\tau }_n$$

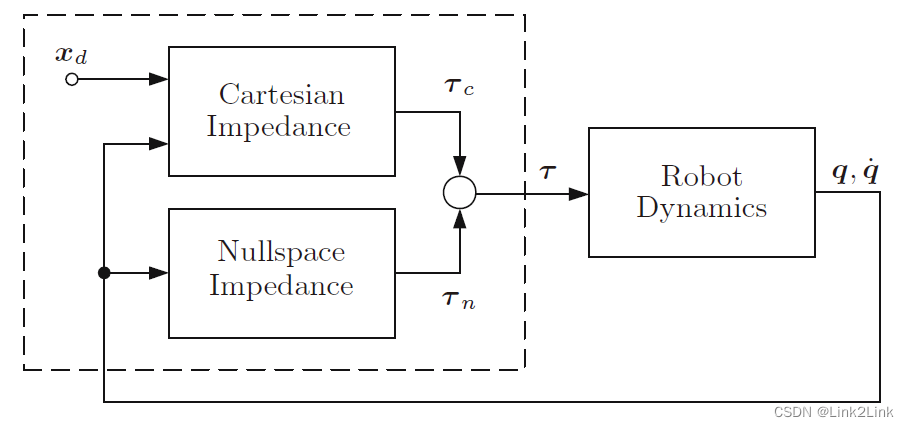
首先定义一个关节空间的阻抗控制
$${\tau }_0=-D_n\dot{q}-K_n(q-q_{d,0})$$
其中$K_n$和$D_n$都是正定对称矩阵，$q_{d,0}$是选定的虚拟稳定点。$q_{d,0}$的选取必须于笛卡尔阻抗控制的给定点一致，既$f(q_{d,0})=x_d$。

但是这个控制不能直接加到原本的笛卡尔空间阻抗上，否则会影响原本的阻抗行为。使用一个投影矩阵
$${\tau }_n=P(q){\tau }_0$$
将其投影到$J(q{)}^T$的值空间中。接下来介绍集中不同的投影矩阵的选取方法。

• 命题4.1 设$\mathcal{A}$是$n\times m$矩阵$A$的值空间， A = { y ∈ R n ∣ ∃ x ∈ R m , y = A x } \mathcal{A}=\{y\in \mathbb{R}^n|\exists x\in \mathbb{R}^m,y=Ax\} A={y∈Rn∣∃x∈Rm,y=Ax}。另$G\in {\mathbb{R}}^{n\times n}$是一个对称正定矩阵，其定义了一个${\mathbb{R}}^n$上的度规。则矩阵
  $$P=A{\left(A^{T}GA\right)}^{-1}{A}^{T}G$$
  是一个投影矩阵，其将一个${\mathbb{R}}^n$上的元素正交投影到$\mathcal{A}$上(相对于$G$)。对应的，投影到正交补空间${\mathcal{A}}^{\perp }$饿投影矩阵是
  $$P_c=I-P$$
  这里需要额外解释的一点，正交的定义是基于内积的，两个向量内积为0即是正交。而内积的定义主要所谓的度规，例如常用的度规$G=I$,因此谈正交性时需要指明度规，既此处的相对于$G$的正交性实际说的是在度规$G$的衡量下是正交的。

静态零空间映射

期望的映射矩阵$P(q)$应使得力矩向量${\tau }_n=P(q){\tau }_0$正交(相对于给定的度规$G(q)$于笛卡尔力矩${\tau }_c=J(q{)}^T{F}_{img}$,既满足关系${\tau }_c^{T}G(q){\tau }_n$=0。显然其需要的矩阵等式为
$$J(q)G(q)P(q)=0$$
$Z(q)=[z_1(q),......,z_r(q){]}^T$中的$r$个向量张成了雅克比的零空间。$P(q)$的一个可行的选择是到$G(q{)}^{-1}Z(q{)}^T$的值空间的映射。
这个结论不太直观，这里只做个检验，假设$P(q)$是到$G(q{)}^{-1}Z(q{)}^T$的值空间的映射，下面用
$$\begin{gathered} Px⟷G^{-1}{Z}^{T}x \\ \Rightarrow GPx⟷Z^{T}x \\ \Rightarrow GPx⟷\left[z_1,......,z_r\right]x \\ \Rightarrow JGPx⟷\left[J{z}_1,......,J{z}_r\right]x \\ \Rightarrow JGPx=0 \end{gathered}$$
因为对任意$x$都成立，因此$JGP=0$
利用命题4.1的结论，可得到投影矩阵（为了公式简介，省略自变量$q$）
$$P_1(q)=G^{-1}{Z}^T(Z{G}^{-1}{Z}^T{)}^{-1}Z$$
这里$P_1(q)$仅仅依赖于运动学，动力学部分没有考虑进来，因此度规$G$可以任意选择，如果选择欧式度规并且$Z(q)$中的$z_i(q)$是正交基底，则这个映射简化为
$$P_1(q)=Z(q{)}^{T}Z(q)$$

动力学一致性映射

在只考虑运动学的情况下才可以任意选择度规，在有动力学的情况下需要考虑笛卡尔空间的加速度和关节转矩之间的关系。给上面的动力学模型左右同乘$J(q)M(q{)}^{-1}$，同时将$\ddot{x}=J(q)\ddot{q}+\dot{J}(q)\dot{q}$代入，得到
$$\ddot{x}-\dot{J}(q)\dot{q}+J(q)M(q{)}^{-1}\left(C(q,\dot{q})\dot{q}+g(q)\right)=J(q)M(q{)}^{-1}\left(\tau +{\tau }_{ext}\right)$$
从这个表达式可以发现，关节力矩会被$J(q)M(q{)}^{-1}$投影到末端上，这不是我们希望的，这个称作动力学一致性(dynamically consistent)，既需要满足
$$J(q)M(q{)}^{-1}P(q)=0$$
根据前面讨论，$P_1(q)$满足$J(q)G(q)P_1(q)=0$，因此直接选$G(q)=M(q{)}^{-1}$，这个度规称作自然度规，得到映射(省略自变量$q$)
$$P_3(q)=M{Z}^T(ZM{Z}^T{)}^{-1}Z$$

另一个映射方法

另一个满足动力学一致性的零空间映射来源于零空间与值空间的关系

前面走的是上边这条路，但是我们知道$J$的零空间是$J^T$值空间的正交补。因此可以使用命题4.1的后一半来实现映射，有
$$P_4=I-J^T{\left(J{M}^{-1}{J}^T\right)}^{-1}J{M}^{-1}$$
这种方法避免了计算零空间的基$Z(q)$，但是需要计算惯量矩阵$M$的逆，因此其计算复杂度更高，一般不用于实时环境下，而$P_3$中$ZM{Z}^T$是个$r\times r$的逆矩阵计算。并且不难证明$P_3=P_4$。

4.3 任务空间扩充方法

这种方法存在耦合问题，因此不常用，仅简单记录一下。
任务空间扩充方法直接扩展任务空间的坐标$x=f(q)$。如果能找到一组合适的坐标$n(q)$使得
$$\begin{gathered} y=\left[\begin{array}{c}x\\ n\end{array}\right] \\ \dot{y}=J_c\left(q\right)\dot{q}=\left[\begin{array}{c}J\left(q\right)\\ \frac{\partial n\left(q\right)}{\partial q}\end{array}\right]\dot{q} \end{gathered}$$
中的雅克比矩阵$J_c(q)$可逆，冗余控制问题就可以简化为非冗余情况。但是$n(q)$的选择是个难题，因为一般情况下$J_c(q)$相比于$J(q)$有更多的奇异点。

4.4 关节空间分解方法

关节空间分解方法不是在人物空间中扩充坐标$x$，而是扩充任务速度$\dot{x}$。
$$\left[\begin{array}{c}\dot{x}\\ v_n\end{array}\right]=J_N\left(q\right)\dot{q}=\left[\begin{array}{c}J\left(q\right)\\ N\left(q\right)\end{array}\right]\dot{q}$$
同样，暂时不进行更加详细的研究