弹珠游戏的数学建模

系统简介

随着时代的发展，人们日益注重儿童的培养，各种开发大脑的益智游戏应运而生，弹珠机便是其中之一，本文所描述的弹珠机是一种类似物理弹球类的实体游戏机器，以能量守恒、概率论和数理统计为理论基础建立数学模型进行研究。通过反复多次对实体机器的体验操作并记录数据作为研究方法，研究对弹珠机施加的初始力的大小与弹珠最终掉落洞口位置之间的关系，分析运动过程中弹珠发生碰撞产生的能量损耗以及弹珠以不同方式从钉板掉落等因素对实验产生的影响。最终达成通过调整初始力来控制弹珠落点的实验目的。弹珠游戏对于开发儿童大脑，锻炼孩子手脑并用的能力有着重要的意义，让孩子在游戏娱乐的同时感受到数学之美，物理之美。
关键词 能量守恒 概率论 数理统计 能量损耗

引 言

弹珠机的历史算是很久远的了，始创于日本，是一种集娱乐与博彩愈一体的机器，很快弹珠机店便已经遍布日本大大小小各个角落，在很长一段时间里深受成人玩家的喜爱。不久之后又相继引入到台湾和大陆，弹珠机的玩法得到普及以及简化最后逐渐演变成了只供小朋友游戏的儿童式弹珠机。现在大陆很多电商平台都能买到，儿童弹珠机的弹珠有钢珠，玻璃球之分，弹珠台有木质，塑料之分。经过市场几年的筛选以及成本等众多因素的考虑，其中玩钢珠和木质的弹珠机逐渐不受欢迎而慢慢淘汰，如今市面上的大多都是玩玻璃珠和塑料材质的弹珠机。
在2009年底，弹珠机（见图1）才正式被引入中国大陆，经过了游戏方式规则的改变和外观材质等的进化，最终应用于中国儿童娱乐行业。不确定性、预判性、挑战性都很高，可以考验和锻炼儿童的眼手合一的能力。仅在方寸之间便能体会无穷乐趣，因其特有的游戏机制，受到广大儿童的欢迎并且迅速蓬勃发展。如今在动漫之都广州，深圳，中山等地的大街小巷里都能看到它的身影。

图1 弹珠机
1 游戏规则及参数符号
1.1 游戏规则
玩者投币一元，机器会出来五颗玻璃珠，把玻璃珠放进投珠口中，位于正平面上的倍数灯（2、3、4、5）与钉板底部上的10个洞口灯就会开始闪烁。此时按下确定按钮，机器将随机选定倍数与洞口灯，拉动右下角弹簧拉杆，把玻璃面板（见图2）内的玻璃弹珠弹入通道后进入钉板，若最后掉落在先前已选定的亮红灯的洞口，即可获得其相应倍数的玻璃球，中奖所得的玻璃弹珠可以重复使用。

图2 弹珠机游戏面板
1.2 弹珠机各部件参数
（1）弹珠机游戏面板与水平面呈角。
（2）弹珠重量约20克，直径约2cm，材质为玻璃。
（3）弹珠机主体部分均塑料材质，不考虑摩擦力。
（4）主界面从顶部到底部长约25cm，其中直线轨道长约20cm，弯道近似一个四分之一圆，半径约为5cm，轨道宽约2.5cm。（见图3）
（5）第一排钉板到底部的距离为15cm，第一排钉板有9个钉点、8个通口，长约20cm，各个钉点之间的距离均为2.5cm；第二排钉板与第一排相距3.75cm，比第一排钉板多1个钉点和1个通口，且每个钉点正好落在第一排两个钉点的正下方中间位置；第三排钉板比第二排多1个钉点和1个通口，且每个钉点正好落在第二排两个钉点的正下方中间位置；第四排钉点分布与第二排钉点分布一致，最底下一层为洞口，洞口的个数以及距离与第三排钉板一致，正好10个洞口。（见图3）

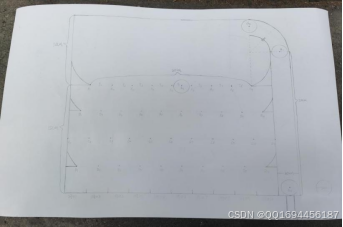
图3 弹珠机游戏面板结构手绘图
1.3 符号说明
表1 符号说明
符号 含义 单位
初始拉力
劲度系数
弹簧的伸长(或缩短）的长度
动能
势能
弹珠的直径
弹珠的质量
直线轨道的长度
通口/轨道的宽
弹珠的初速度
弹珠到达直线轨道顶端时的瞬时速度
弹珠即将进行平抛运动飞出弯道时的位置 /
弹珠下落至第一排钉板时的位置 /
处弹珠的速度
处弹珠的速度
与水平方向的距离
与垂直方向的距离
平抛运动后水平方向的速度
平抛运动后竖直方向的速度
与之间运动的时间
重力加速度
第一排钉板与底部洞口的距离
第一排钉板距离洞口底部的竖直距离

2 问题重现

问题一：任意给定的一个初始力，建立数学模型，给出弹珠落入各个目标洞口的概率与力的关系。
问题二：游戏开始后，当机器随机确定通道灯（即指定目标洞口），用多大的初始力，可以使弹珠落入目标洞口？

3 问题分析

3.1 问题一分析
根据整个游戏的流程，可将弹珠的运动过程分成三部分：
（1）游戏开始时，任意给定一个初始力，弹簧拉杆在力的作用下做功，产生的弹性势能[1]全部转化为弹珠的初始动能，使得弹珠能够克服重力作用，沿直线轨道向上作匀减速运动，部分动能转化为重力势能[2]。
（2）弹珠由直线轨道进入弯道，与轨道会发生碰撞，碰撞时伴随着速度的减小以及大量的能量损耗。弹珠飞出弯道后，以平抛运动下落到第一排钉板的某个位置。初动能越大，碰撞后的能量损耗也会增大，多次实验并测量数据找出两者之间的关系。根据能量守恒[3]，不考虑摩擦力，可以得出弹珠在第一排钉板时的动能加上重力势能以及碰撞损耗的能量等于弹珠的初始动能。从而可以找出初始力与之间的关系式
（3）弹珠落在第一排钉板时，可能落在钉点上也可能直接从通口滑落，可能落在靠中间的位置也可能落在靠边上的位置。一旦弹珠下落的位置确定，则可以将其看成是一个类似高尔顿顶板实验[4]的运动模型，从而求得最终落在各个洞口的概率分布。
3.2 问题二分析
由问题一求解可以得到弹珠在第一排钉板时掉入的通口与最终落入目标洞口的概率分布规律。问题二可以看作是问题一的逆问题。当选定最终掉落的洞口，可以反推出弹珠最终掉入指定目标洞口概率最大时弹珠应从第一排钉板的哪一个通口掉入，从而可以确定的取值范围。再由问题一中得到的初始力与之间的关系式计算出力的取值范围。

4 模型的建立与求解

4.1 弹珠沿直线轨道运动
由于条件限制，弹簧拉杆使用的弹簧的劲度系数[5]并不知晓，需要先确定弹簧的劲度系数。弹簧的劲度系数与很多因素有关，如弹簧的材质、弹簧丝的粗细、弹簧圈的直径等等。这些数据测量难度较大，于是考虑通过实验测量数据，运用胡克定律[6]计算弹簧的劲度系数。
用拉力器的一端勾住弹簧装置，缓缓拉动拉力器。当拉力器显示20N时，测量弹簧拉杆的伸长量约为1厘米。根据胡克定律计算，可以得出该弹簧拉杆的弹簧的劲度系数大概为2000N/m。
在实验条件不变的前提下，多次进行实验。发现只要拉力器显示20N时，弹簧拉杆的伸长量均约为1厘米。又选取了不同的力进行实验，根据胡克定律计算出弹簧的劲度系数基本在2000N/m附近，故取。
因为不考虑摩擦力，在初始力的作用下，弹簧击打弹珠后，弹簧的弹性势能全部转化为弹珠的动能。即

（1）
弹珠获得初速度，克服重力作用，以加速度沿直线轨道向上做匀减速直线运动。由能量守恒定律得，到达直线轨道顶端时的瞬时速度为。
4.2 弹珠沿弯道运动后飞出，做平抛运动[7]
弹珠进入弯道后，作圆周运动，与轨道碰撞时，会产生能量损耗。当弹珠飞出弯道即将进行平抛运动时，记此时弹珠的位置为，速度为。当弹珠进行平抛运动，下落至第一排钉板时，记此时弹珠的位置为，速度为，与之间水平方向的距离记为，垂直方向的距离记为。平抛运动过程中弹珠水平方向的瞬时速度为，垂直方向的瞬时速度为。显然，它们满足下列等式：
（2）

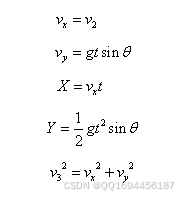
（3）
（4）
（5）
（6）
根据能量守恒定律知

（7）
其中，表示弹珠在位置相对于弹珠初始位置的重力势能，表示弹珠在弯道中碰撞损失的能量。因为是未知的，不易得到。下面取一些初始力进行实验，记录在相同的力作用下和的值，以及不同的力作用下和的值，运用公式（1）—（7）计算。
以为例，重复多次实验，均测量得到约为6.25cm，第一排钉板是固定的，所以等于9cm，即第一排钉板到弹珠机顶部挡板的距离减去弹珠的半径。

（其中由公式（2）—（6）计算）

而，所以。
再取不同大小的力进行实验，发现当力过小时，弹珠在上升的过程中，或者进入弯道时速度不够会掉落回起点；当力足够大，使得弹珠冲出弯道，比值基本在0.84附近。由实验结果可以得知当初始力在适当的范围（确保弹珠可以冲出弯道）内，比值始终接近0.84。即。由公式（1）—（7）知，可以通过改变初始力的大小直接算出弹珠落在第一排钉板的准确位置。
假设弹珠能够完成实验，那么一定会掉落在第一排钉板的某个位置，由于第一排钉板是固定的，所以弹珠落在第一排时的重力势能是固定不变的，。又，所以由公式（7）得，。
再由（2）—（6）有，

                                                           （8）

上式给出了初始力与弹珠落在第一排钉板的位置之间的关系。令，求得；令，求得。
所以弹珠要完成这个实验，则施加的初始力只要在19.6N到23.9N之间即可。
4.3 钉板实验
将第一排钉点从左至右分别标记为，第二排钉点从左至右分别为，第三排钉点为，第四排钉点为，第一排通口从左到右分别标记为，最后洞口从左到右分别为洞口1～10。
当弹珠经过平抛运动下落至第一排钉板的时候会出现两种情况：（1）弹珠直接从某一处通口掉落；（2）弹珠碰撞第一层钉点再掉落。
4.3.1 弹珠从通口直接掉落
弹珠直接从通口往下掉落，落在第二层钉板时与钉点发生碰撞，此时弹珠随机向左向右掉落，下落到第三层钉板再次碰撞，随机向左向右掉落，直至最后掉落到洞口。
通过实验，我们发现，弹珠从最边上的通口（或）下落和与从中间的通口（除了和）下落是有区别的。假设弹珠从通口掉落，那么在它下落的过程中畅通无阻，随机向左或向右掉落，如果弹珠一直向左边的通口掉落，那么最终会落到1号洞口；如果弹珠一直向右掉落，那么最终会落在5号洞口。所以当弹珠直接从通口掉落时，最终可能会落入洞口1~5中的某一个。但是如果弹珠从通口或下落，由于边框的限制，弹珠在落到第四层钉板时会被强制从仅有的通口掉落，导致最终掉落洞口的只存在四种可能性。我们先讨论除了和的其他六个通口的情况。
假设弹珠从通口掉落，我们将通过此通口的的概率记作1。落到第二排钉板必定与发生碰撞，然后随机向左或向右掉落，概率均为。落到第三排钉板可能与或发生碰撞后随机向左向右掉落的概率均为，但是碰撞向右掉落与碰到向左掉落的是同一个通口，所以，弹珠通过与的通口、与的通口、与的通口的概率分别、、，然后再掉落下一层。总结规律会发现：在弹珠经过通口时，经过每个通口的概率都是通向这一通口的上一次通口的概率的（见图4）。

图4 概率分布图
由杨辉三角[11]（见图5）的数字排列规律，图4中的概率值也可找到数字排列的规律（见图6）。

图5 杨辉三角

4.5 问题二求解
从表2、表3可以看出，当已知选定的洞口，只需要把每一行选中的洞口的概率相加作比较，找出最大概率情况的那一行，则可以知道这种概率情况下弹珠在第一排钉板的下落位置。再根据初始力与之间的关系式反推出的取值范围。
4.6 数值算例
（1）假设初始力，求弹珠下落在哪个洞口的概率最大？
通过前面建立的模型，我们已经得出初始力与之间的关系式（8），于是有

（9）

5 模型的评价

（1）该模型分成三个部分研究弹珠机并模拟实验，分别是物理模块，实验中包含弹性势能，动能，重力势能的转变，碰撞的能量损耗等物理量，其次是数学模块，包括杨辉三角，排列组合，概率论等数学知识，以及计算机模块，通过matlab数学软件，对数据进行模拟整合。三个模块相辅相成，使得实验更加合理更加具有一般性。
（2）由于市面上弹珠机的型号以及结构都不尽相同，并且为了方便实验研究和数据模拟，对弹珠台结构进行一定简化，所以该模型并不一定适用任一型号弹珠机。
（3）进行实验时，因缺少精密测量仪器，可能导致采集的数据存在测量误差，在计算过程中也有舍入误差存在，造成最终结果可能存在偏差。
（4）由于弹珠以及轨道较为光滑，实验中我们忽略了摩擦力，导致碰撞损耗比实际情况要大。