Bayesian framework 贝叶斯框架 （R）

写在前面

本文介绍了 Bayes' theorem（贝叶斯定理），Bayesian inference（贝叶斯推理），Bayesian regression Model （贝叶斯回归模型） 等。

贝叶斯定理大家都耳熟能详，高中数学甚至都有涉及，即：用先验概率和条件概率求出另外的条件概率。

但贝叶斯推理和回归模型我认为是一个比较trick 的内容。

用一张图解释本文的内容：

一些术语

prior :   1 happening or existing before sth else or before a particular time  ,  2 already existing and therefore more important；

likelihood : 参考我之前的博客；

posterior : located behind sth or at the back of sth

Bayes' theorem 贝叶斯定理

简单来说就是用先验概率和条件概率求出另外的条件概率。

Bayesian inference

将贝叶斯定理应用在统计分析中, 即模型参数是未知量, 而且它们的先验分布需要被（手动/经验地）指定 — this is Bayesian inference.

（在贝叶斯框架中，我们讨论的是模型参数的概率分布 ，注意，在那些常见的框架中，如以MLE为基础的GLM，模型参数是 fixed non-random quantities ，数据才是遵循某种概率分布 ，这是两者显著的不同。

一个粗鲁的解释就是：我们有一堆观测数据，我们揣测这个数据可能符合某种模型分布，如正态。泊松等，然后模型的参数也被我们 揣测地 定了下来， 然后我们用观测数据和这个我们揣测的模型 去收敛训练， 最后我们得到了 posterior ，这个 posterior，是 我们根据观测数据收敛训练，得到的模型的参数 ，注意我们得到的是参数的分布，而不是点估计。

 

更多的可以参考这里。）

假设：

1 观测量，即数据 ，是 x；

2 位置量是θ，这个 θ 可以代表模型参数，数据中地缺失值，误测值等；

基于我们上面的假设，

首先我们提出 likelihood ：p(x | θ)

然后我们从贝叶斯定理的角度观察 ： θ 是未知的，所以它需要有（被手动/经验地指定）一个概率分布，用来表示这个 不确定性； x 是已知的，所以它是条件（condition on it），我们得到 posterior distribution ：

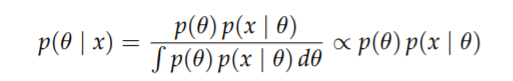
所以总的来说，我们首先指定了一个  prior distribution p(θ), 表达了我们在看到数据之前对θ不确定性的预估. The posterior distribution p(θ | x), 表达了我们在看到数据之后对θ不确定性的预估。

很明显：1 我们的 posterior 是prior 和 data （likelihood） 的居中选择，2 如果我们的数据越多，我们的 data （likelihood ）的 影响力就越大，prior 影响力就越小 （比如你认为 它们都是好的，但搞了一堆观测数据发现它们基本都是坏的，那推论 必然更容易是 它们是坏的）