使用插值方法（scipy.interpolate）和三维数据构造二元函数

背景

在上一篇博客中介绍了使用插值方法和二维数据构造一元函数，在定义域内，可以构造出能实现任意我们想要的变化规律的函数。当自变量是二维或多维时，也可调用scipy.interpolate里面的方法来构造高维的曲面或超曲面，并使构造出的函数在定义域内实现我们想要的规律。

需要说明的是，如果要构造函数，那使用的多维数据中的维度，本身要有对应关系。例如有三维数据点(a,b,c)，要将a,b作为自变量，c作为因变量来构造二元函数，则每一个数据的a,b维度，都能和c维度对应，才能构造函数；如果一个数据点的a,b对应的是一个随机的c，或者说不确定对应到哪个数据点的c，那就不能构造函数，因为函数是确定的对应关系。

方法1

下面先给出代码，再对结果进行说明。

其中bisplrep和RectBivariateSpline可以通过超参数s的调整来决定是否进行平滑插值，s越大插值函数越平滑，在定义域内对数据点的拟合程度越低一点。

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt


# 用三维插值构造函数，unstructured data, no sequenced, random------------------------------------------------------
def bivar_interp(x, y, z, xnew, ynew, xb=None, xe=None, yb=None, ye=None, kx=3, ky=3, s=None):
    """
    根据给定的三维数据点构造曲面，同时传入新的二维自变量得到新的应变量。
    :param x: 用于构造插值曲面的点的x坐标
    :param y: 用于构造插值曲面的点的y坐标
    :param z: 用于构造插值曲面的点的z坐标
    :param xnew: 根据已构造曲面，输入新的点的x坐标
    :param ynew: 根据已构造曲面，输入新的点的y坐标
    :param xb: x最小值，输入的x序列不能低于该下限，用于构成定义域的边界
    :param xe: x最大值，输入的x序列不能高于该上限，用于构成定义域的边界
    :param yb: y最小值，输入的y序列不能低于该下限，用于构成定义域的边界
    :param ye: y最大值，输入的y序列不能高于该上限，用于构成定义域的边界
    :param kx: x维度样条的灵活性，取值1~5，越大越灵活，插值或拟合时对给定点的逼近程度越高，但在非给定点的振荡性越大；
    :param ky: y维度样条的灵活性，取值1~5，越大越灵活，插值或拟合时对给定点的逼近程度越高，但在非给定点的振荡性越大；
        (kx+1)*(ky+1) <= len(x)
    :param s: 非负平滑因子，取值越大曲面越平滑，越近0对给定点的逼近程度越高；当s=0时则为完全插值，不具有拟合特性。
        通常取值为[len(x)-np.sqrt(2*len(x)), len(x)+np.sqrt(2*len(x))]，当kx，ky取值越大时，s当取值越大，反之s应越趋近0.
    :return: 新输入点对应的z值
    """

    try:
        if (kx + 1) * (ky + 1) > len(x):
            raise Exception('len(x)应 >= (kx+1)*(ky+1)')
        if s is None:
            surf_func = interpolate.bisplrep(x, y, z, xb=xb, xe=xe, yb=yb, ye=ye, kx=kx, ky=ky,
                                             s=len(x) + np.sqrt(2 * len(x)))
        else:
            surf_func = interpolate.bisplrep(x, y, z, xb=xb, xe=xe, yb=yb, ye=ye, kx=kx, ky=ky, s=max(s, 0))
        znew = interpolate.bisplev(xnew, ynew, surf_func)
        return znew
    except Exception as e:
        print(e)


x = 100 * np.random.random(30)
y = x
z = 10 * np.random.random(30)

xnew = x
ynew = y
znew = []
for i in range(len(xnew)):
    znew.append(bivar_interp(x, y, z, xnew[i], ynew[i], kx=3, ky=3, s=0))

plt.figure()
ax = plt.axes(projection='3d')
ax.scatter3D(x, y, z, edgecolor='red')
ax.plot3D(xnew, ynew, znew)
plt.show()

plt.figure()
ax = plt.axes(projection='3d')
ax.scatter3D(x, y, z, edgecolor='red')
xnewmesh, ynewmesh = np.meshgrid(xnew, ynew)
znewmesh = np.meshgrid(znew, znew)
ax.plot_surface(xnewmesh, ynewmesh, znewmesh[0])
plt.show()

print('各点偏差比：', '\n', (z - znew) / z, '\n')
print('平均绝对偏差比：', '\n', sum(abs((z - znew) / z)) / len(z), '\n')

结果分析1

图1

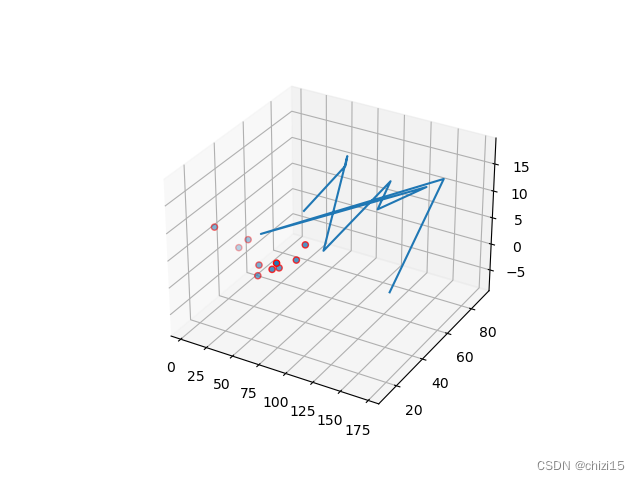
图2

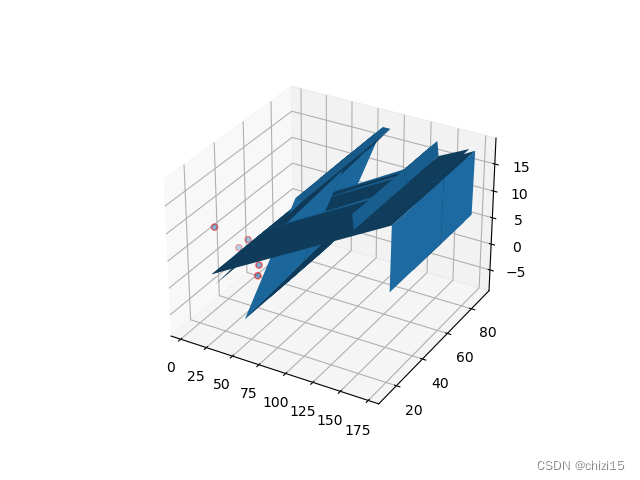
图3

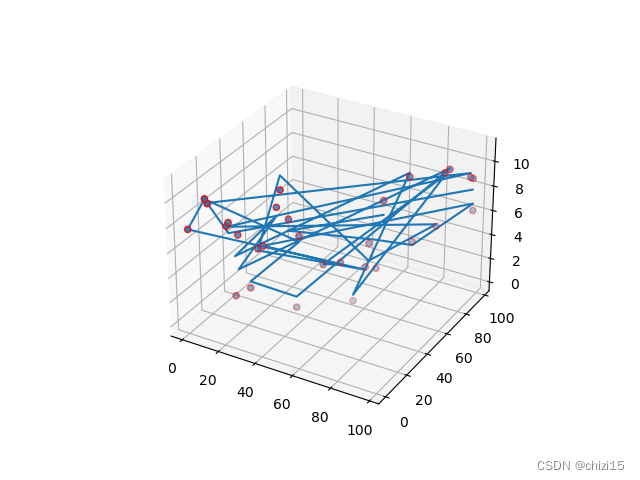
图4

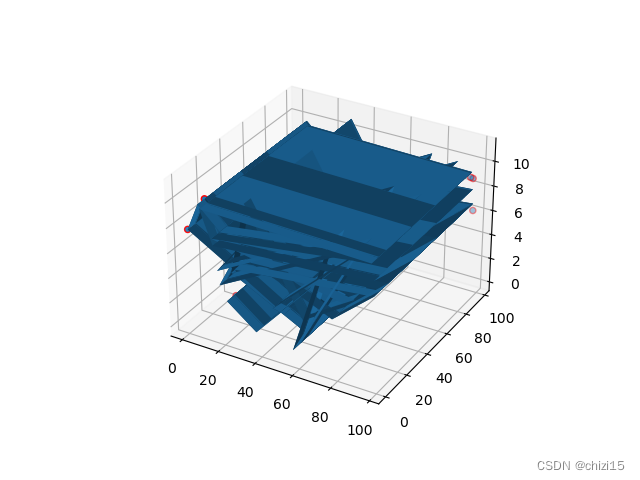
上面两种情况下（图一图二和图三图四），插值函数的应变量和原始数据的Z值之间的差值是比较大的，对于图三图四的情况，平均偏差比达到了30%；这是因为输入插值函数的自变量数值是无序的，没有按照升序或降序排列，就导致了插值函数会由多个曲面或平面组合而成。

各点偏差比：
[-7.90546575e-02 2.35957959e-01 -7.58730255e-02 1.41800619e-01
-6.50625299e-02 -1.76365768e-03 5.42502574e-03 -1.64974872e-01
-2.25054271e-01 -5.13678873e-02 -9.40811174e-03 2.43468805e-01
-7.92869814e-01 2.42361263e-02 -2.04775707e+00 1.44441633e-01
-1.05379438e+00 2.30835751e-01 3.53757216e-01 -6.32020924e-01
1.08860158e-02 4.33972085e-02 2.45153374e-01 5.08375107e-02
1.81743005e-01 4.48640958e-03 -2.90772298e-02 -2.28021621e-03
-1.58333107e+00 3.88827458e-01]

平均绝对偏差比：
0.30396479434337614

方法2

# 用三维插值构造函数，structured data, sequenced------------------------------------------------------------------------------
def Rosenbrock(x):
    x = np.asarray(x)
    r = np.sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0, axis=0)
    return r

x = np.linspace(-1, 1, 30)
X, Y = np.meshgrid(x, x)  # X,Y是互为转置的二维数组，以铺满三维坐标轴的水平面
interp_func = interpolate.RectBivariateSpline(X[0], X[0], Rosenbrock([X, Y]) + 1, kx=3, ky=3, s=len(x) ** 2)

plt.figure()
ax = plt.axes(projection='3d')
ax.scatter3D(X, Y, Rosenbrock([X, Y]) + 1, edgecolor='red')
ax.plot_surface(X, Y, interp_func(X[0], X[0]))
plt.show()

print('各点偏差比：', '\n', (Rosenbrock([X, Y]) + 1 - interp_func(X[0], X[0])) / (Rosenbrock([X, Y]) + 1), '\n')
print('平均绝对偏差比：', '\n',
      sum(sum(abs((Rosenbrock([X, Y]) + 1 - interp_func(X[0], X[0])) / (Rosenbrock([X, Y]) + 1))))
      / (len(X) * len(Y)), '\n')

结果分析2

图5

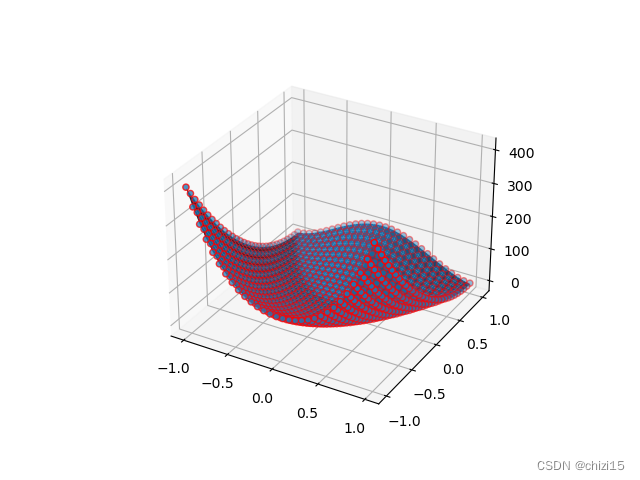
平均偏差比：
0.07219041607484152

从图5可以看到，当输入插值函数的自变量按顺序排列时，插值函数的应变量和原始数据的Z值之间的差值就很小了，平均偏差比只有7.22%。

总结

1. 自变量保持顺序的方式传入插值函数，所得函数就可以保持原始数据应有的顺序和规律性；如果乱序传入，因为插值函数是按逐个数据点的顺序进行插值，所得函数就可能被切分为很多零散的曲面或超曲面。
2. 平滑因子s和样条灵活性kx和ky是插值函数最重要的超参数：s越大，函数越平滑，对数据点的拟合程度就越不是完全拟合；kx,ky越大，函数越灵活，（如kx=ky=1时则为平面插值），但也越可能出现振荡。