
- 由图①可知,当一阶导函数在某点(即驻点)处为0,二阶导函数在该点处小于0时,原函数在该驻点处取极大值;
- 由图②可知,当一阶导函数在某点(即驻点)处为0,二阶导函数在该点处大于0时,原函数在该驻点处取极小值;
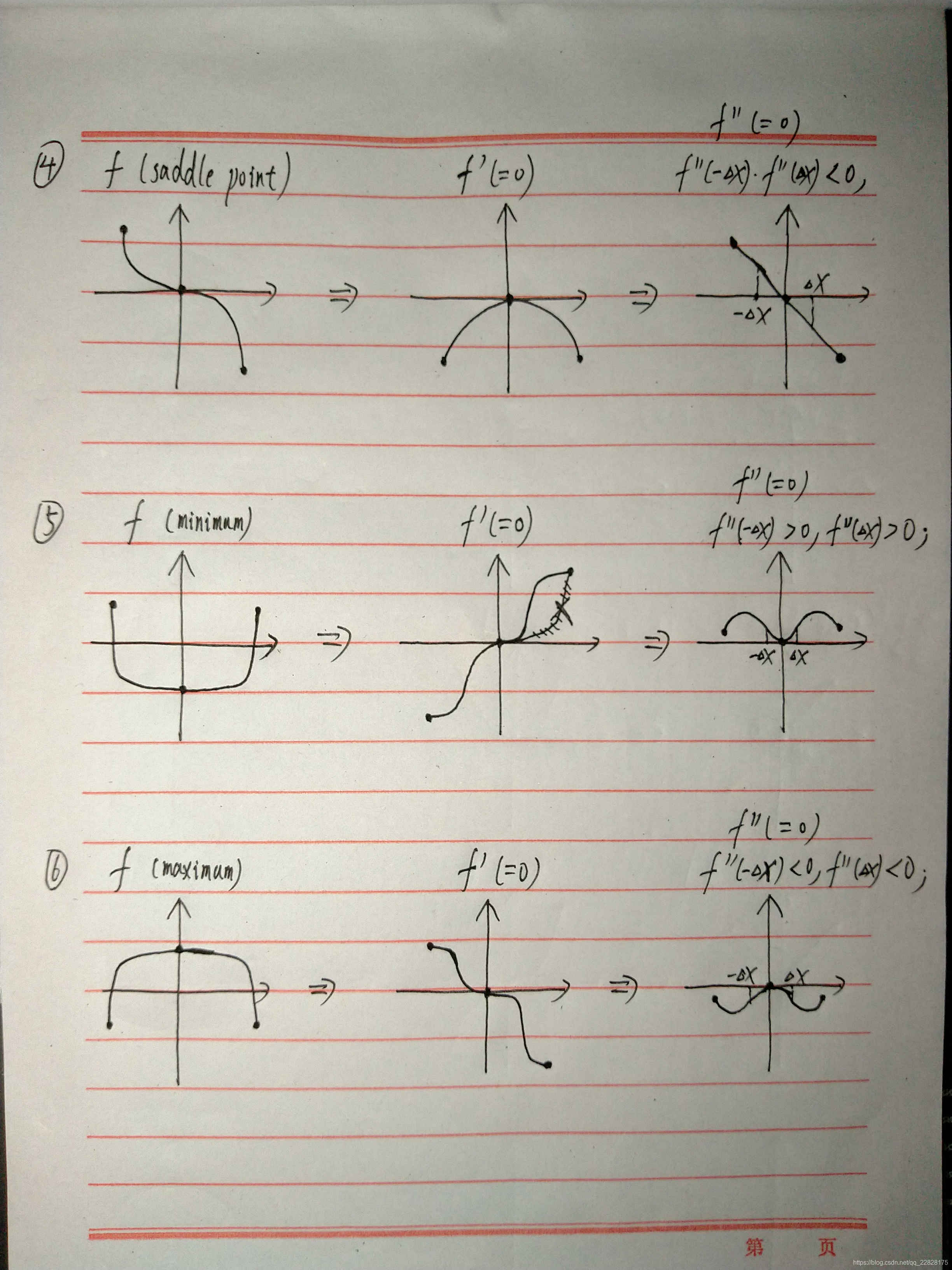
- 由图③④可知,当一阶导函数在某点(即驻点)处为0,二阶导函数在该点处也为0,且以该点加减一个非常小的δx得到两点,二阶导函数在这两点处的值异号时,该驻点为原函数的鞍点;
- 由图⑤可知,当一阶导函数在某点(即驻点)处为0,二阶导函数在该点处也为0,且以该点加减一个非常小的δx得到两点,二阶导函数在这两点处的值同号且都大于0时,该驻点为原函数的极小值点;
- 由图⑥可知,当一阶导函数在某点(即驻点)处为0,二阶导函数在该点处也为0,且以该点加减一个非常小的δx得到两点,二阶导函数在这两点处的值同号且都小于0时,该驻点为原函数的极大值点;
- 当驻点处二阶导数为0时,还可求其三阶导、四阶导等,直到可以判断出原函数在驻点是极小值点、极大值点还是鞍点为止。

























 505
505

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










