泰勒公式与极限问题：从基本原理到张宇“狗3定理”详解

泰勒公式与极限问题：从基本原理到张宇“狗3定理”详解

---

在高等数学的极限与近似计算中，泰勒公式作为一种强有力的工具，帮助我们将复杂的函数表达成多项式形式，以便于近似求解和分析函数的行为。特别是在处理函数的极限时，泰勒展开能够有效简化计算，极大地提高了求解效率。在张宇老师的讲解中，泰勒公式中的三阶展开被幽默地称为“狗3定理”，并通过生动的例子向学生展示了泰勒展开的实际应用。

本文将详细介绍如何通过泰勒公式处理极限问题，深入分析张宇老师的“狗3定理”，并结合例题带你掌握这些工具在考试中的运用。

---

1. 问题背景：泰勒展开与极限

题目描述：

我们要处理一个包含 $\sin x$ 函数的极限问题，具体题目如下：

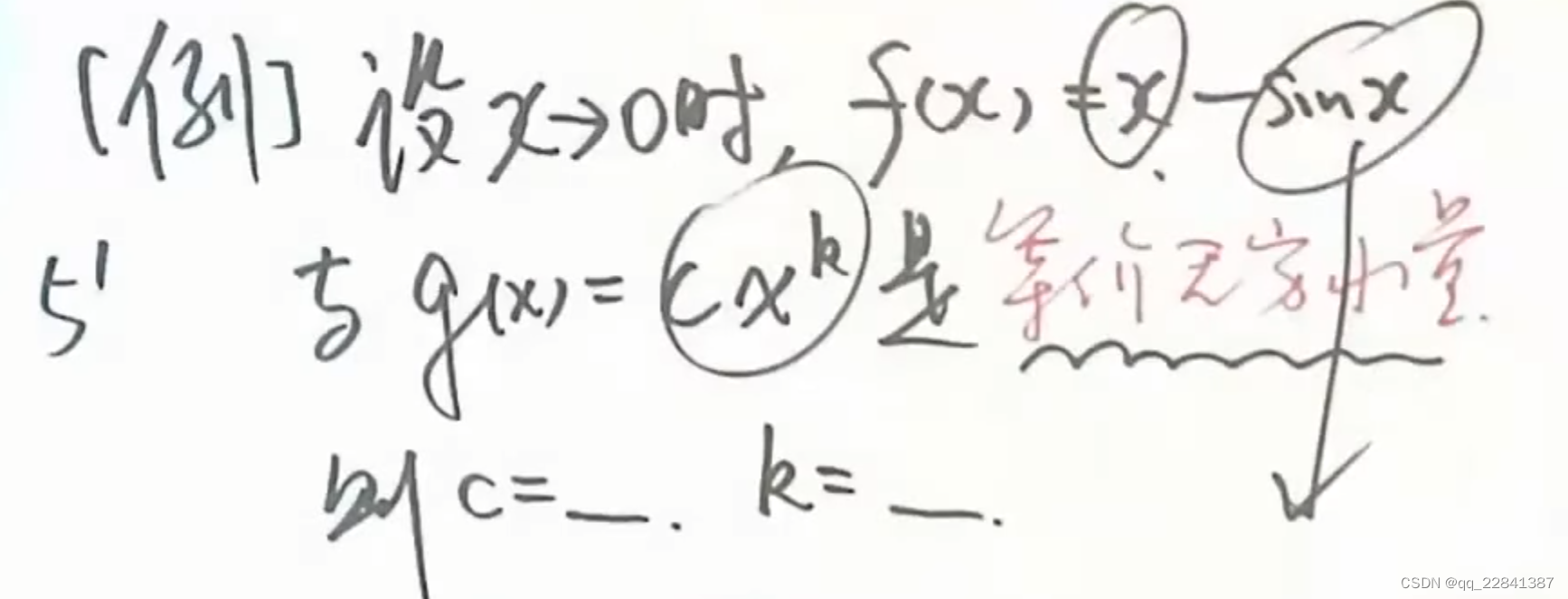
题目分析：

该问题涉及 $\sin x$ 和 $x$ 的差值。由于 $\sin x$ 和 $x$ 在 $x\to 0$ 时具有非常接近的行为，因此我们自然联想到可以使用泰勒公式对 $\sin x$ 进行展开，从而得到较为简洁的表达式。

泰勒展开的概念回顾：

泰勒公式是一种将一个函数展开为幂级数的表达方式，具体形式为：

$$f(x)=f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\cdots +\frac{f^{(n)}(a)}{n!}(x-a{)}^n+o((x-a{)}^n)$$

对于 $\sin x$，在 $x=0$ 处的泰勒展开为：

$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots$$

---

2. 通过泰勒展开解决问题

特别处理：$x-\sin x$

当我们在题目中看到 $x-\sin x$ 时，立即想到使用泰勒展开处理 $\sin x$。将 $\sin x$ 的泰勒展开代入，得出：

$$\sin x=x-\frac{x^3}{3!}+o(x^3)$$

那么：

$$x-\sin x=x-\left(x-\frac{x^3}{3!}+o(x^3)\right)=\frac{x^3}{6}+o(x^3)$$

因此，当 $x\to 0$ 时，$x-\sin x$ 的值接近于 $\frac{x^3}{6}$。这就是高阶无穷小的概念。

计算极限：

我们可以直接计算：

$$\underset{x\to 0}{\lim }\frac{x-\sin x}{x^3}=\underset{x\to 0}{\lim }\frac{\frac{x^3}{6}+o(x^3)}{x^3}=\frac{1}{6}$$

---

3. 张宇“狗3定理”的运用

什么是“狗3定理”？

张宇老师幽默地将三阶泰勒展开的应用称为“狗3定理”，即在处理极限问题时，通过三阶展开来简化计算，尤其是遇到 $\sin x$、$\cos x$ 等函数时。通过泰勒展开，我们可以快速识别高阶无穷小，从而高效求解极限。

例题演示：

解题思路：

1. 识别极限中的“狗”：这里的 $x\to 0$ 时，$\sin x$ 近似 $x$，即 $\sin x$ 是泰勒展开中的主要部分。

2. 使用三阶泰勒展开简化表达式：
   $$\sin x\approx x-\frac{x^3}{6}$$

3. 代入并进行简化：
   $$\underset{x\to 0}{\lim }\frac{x-\sin x}{x^3}=\underset{x\to 0}{\lim }\frac{\frac{x^3}{6}}{x^3}=\frac{1}{6}$$

因此，答案为 $\frac{1}{6}$。

---

4. 重要结论与扩展

通过以上例题的分析，我们可以得出一些重要的结论和技巧，这些结论对处理类似极限问题非常有帮助。

结论 1：$\sin x$ 的泰勒展开（奇函数）

$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots$$

由于 $\sin x$ 是奇函数，它的展开式中只含有奇数次幂项。

结论 2：$\cos x$ 的泰勒展开（偶函数）

$$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots$$

由于 $\cos x$ 是偶函数，它的展开式中只含有偶数次幂项。

数学的统一美：

泰勒公式的展开本质上是一种将复杂函数线性化的过程，具有非常强的通用性。无论是 $\sin x$、$\cos x$ 还是其他函数，通过泰勒展开，我们都能近似地了解它们在某点附近的行为。

---

5. 总结

通过本文的分析，我们深入了解了泰勒公式在处理极限问题中的强大作用。尤其是在计算包含 $\sin x$ 和 $\cos x$ 等函数的极限时，使用泰勒展开可以快速得到近似解。而张宇老师的“狗3定理”通过风趣的讲解，让我们对三阶泰勒展开有了更为直观的认识。

主要收获：

• 使用泰勒展开可以有效处理极限问题。
• 三阶展开，尤其在 $\sin x$、$\cos x$ 的极限计算中非常实用。
• 张宇老师的“狗3定理”让我们在考试中能够快速识别和求解相关问题。

掌握泰勒公式和高阶无穷小的处理方法，将极大提升你在极限、微积分等问题中的解题效率。