【论文精读】Knowledge Transfer with Jacobian Matching

Knowledge Transfer with Jacobian Matching

原文链接：Knowledge Transfer with Jacobian Matching

关于蒸馏法（distillation）可以参考一下以下两篇博文：

蒸馏神经网络(Distill the Knowledge in a Neural Network) 论文笔记

知识蒸馏（Knowledge Distillation）

关于教师-学生类型的迁移学习可以参考阅读下面这篇博文：

深度学习模型压缩方法综述（三）

Abstract

经典的蒸馏（distillation）方法通过匹配输出激活，将表示从教师神经网络（复杂庞大的网络）转移到学生网络（较为简单轻量级的网络）。最近的方法也有将他们的雅可比矩阵或者输出激活值的梯度与输入相匹配的。然而，这涉及到做出一些特别的决定，特别是损失函数得重新设计。在本文中，作者首先证明了通过雅可比矩阵的匹配与带有输入噪声的蒸馏法的等价性，并由此推导出合适的雅可比矩阵匹配的损失函数。然后，作者根据这个分析，通过建立一个最近的迁移学习过程到蒸馏的等价性，将雅可比矩阵匹配应用于迁移学习。然后在标准的图像数据集中实验显示基于雅可比矩阵的惩罚提高了蒸馏法的效果、对噪声输入的鲁棒性和迁移学习的效果。

1. Introduction

知识迁移是指的在相似（或相关联）的数据集下，根据一个已经训练好的神经网络$\mathcal A$的信息，训练另一个网络$\mathcal B$的问题。Hinton et al.用信息蒸馏法使用同一训练集训练不同架构的神经网络实现知识迁移；Pan & Yang在不同的训练集上实现知识迁移。

一个好的蒸馏方法可让我们在保留网络泛化能力的情况下很轻松地将一个网络迁移到另一个网络。这使得我们可以去探索更多的网络结构空间并找到更加简单的网络实现网络压缩等任务。同时一个好的迁移学习方法可以最优化的使用有限的数据。

本文讨论了通过匹配网络输出的雅可比矩阵和输入来改进知识迁移。利用输出的雅可比矩阵进行迁移学习的相关工作也在近年被开展过比如Czarnecki et al.和Zagoruyko & Komodakis的论文，但是这些方法和传统蒸馏方法的联系尚不确定，所以很难确定为什么他们的表现会变好。Li & Hoiem也提出了一种类似于蒸馏法的方法，但这种方法和蒸馏法准确的联系尚不明了，因此很难去预测蒸馏法的改进是否意味着迁移学习效果的提高。

本文章的贡献点主要有以下三点：

1. 作者证明匹配雅可比矩阵的方法是一种传统蒸馏方法的特殊形式，其中输入中存在噪声。
2. 作者证明了Li & Hoiem的方法也可以被看作蒸馏法，这使得可以对这种方法也进行雅可比矩阵匹配。
3. 作者提供了一种方法对实际的深层网络进行雅可比矩阵的匹配，其中进行匹配的网络他们的架构是任意的。

作者通过实验验证了雅可比匹配可以同时帮助蒸馏法和迁移学习效果的提高，同时验证了基于雅可比模的惩罚项可以提高模型对噪声的鲁棒性。

2. Related Work

Czarnecki et al.提出使用目标（应该是蒸馏法中的“软目标”）的高阶导可以帮助提高训练数据的效率，即训练时使用更少的数据。作者在本文中虽然也有类似的声明，但同时作者也证明了这种方法与一般的使用输出激活值匹配的蒸馏法的联系。特别地，作者指出确定使用输出激活值匹配的蒸馏法的损失函数如何也能确定使用雅可比匹配的损失函数。同时Wang et al.、Zagoruyko & Komodakis也都证明了雅可比矩阵能让蒸馏法表现得更好。

Drucker & Le Cun考虑了使用雅可比矩阵的模作为惩罚项。直觉上，这样可以增加模型对输入微小变化的鲁棒性。作者也发现这么做很有效。

知识（信息）蒸馏法表明有温度超参的softmax可以用来在网络间进行知识迁移。Ba & Caruana发现logits（softmax的输入）的平方误差比softmax表现更好，而且基于这个方法，他们用浅层的网络获得了和深层网路同样的效果。Romero et al.和Zagoruyko & Komodakis用不同的方法也证明了可以通过伴随着输出的媒介特征来增强蒸馏方法的效果。Sau & Balasubramanian发现对logits添加噪声对教师-学生模式的迁移学习有帮助，作者也证明雅可比矩阵匹配的方法可以看作是向输入中增加噪声。

3. Jacobians of Neural Networks

这一节介绍了一阶泰勒展开和神经网络雅可比矩阵的背景知识，应该在后面会用到。

考虑方程$f:\mathbb R^D \rightarrow \mathbb R$在$\{x+\Delta x:\left \| \Delta x \right \|\le \epsilon \}$的一阶泰勒展开：

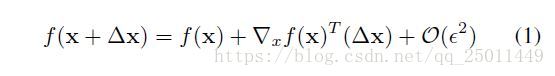
可以利用泰勒展开对神经网络进行线性化处理。要想对神经网络进行线性化处理，就必须将非线性的单元比如激活函数、池化操作进行线性化。

3.1. Special case: ReLU and MaxPool

对于ReLU的激活函数，泰勒展开可以在局部精确地计算，因为ReLU的导数不是1就是0（当然在$z=0$出没有定义）。Max-pooling的激活函数也类似。在泰勒展开式（1）中存在着$\epsilon > 0$使得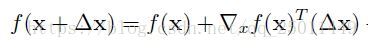

成立。

3.2 Invariance to weight and architecture specification

One useful property of the Jacobian is that its dimensionality does not depend on the network architecture. For $k$ output classes, and input dimension $D$, the Jacobian of a neural network is of dimension $D\times k$. This means that one can compare Jacobians of different architectures.

Another useful property is that for a given neural network architecture, different weight configurations can lead to the same Jacobian.

这里介绍了神经网络雅可比矩阵的两个比较重要的性质：

• 维度不随着网络架构的改变而改变，至于输入和输出的维度有关。因此，这样一来就可以比较不同架构的网络的雅可比矩阵。
• 另一个性质是对于给定架构的网络，不同的权重配置可能得到相同的雅可比矩阵，这是由于网络的冗余性和损失函数非凸性造成的。

如此一来，雅可比矩阵自然就能捕获不同网络映射之间的相似性，这正是知识迁移所需要的。同时输出的激活值同样也很重要。下面这篇文章就要讨论如何把这些值用在知识迁移上。

Distillation

知识蒸馏问题（也就是一种模型压缩的问题）可以有如下的定义：在训练集$\mathcal D$上训练了一个教师网络$\mathcal T$。我们希望利用教师网络中的一些线索在$\mathcal D$上强化学生网络$\mathcal S$。一般地，这些线索包括输出层的激活值或一些中间层。最近有些工作通过雅可比矩阵的匹配来训练$\mathcal S$。但是有两方面的问题尚不明了：

1. 使用怎样的惩罚项。
2. 使用雅可比匹配的思想和一般的蒸馏法（激活值匹配）有什么联系。

为此，作者声明如下：

Claim. Matching Jacobians of two networks is equivalent to matching soft targets with noise added to the inputs during training.

意思是网络间雅可比匹配的效果和训练时输入中加入噪声的“软目标”匹配效果相同。

更具体地，作者提出如下命题：

上面这个命题就是“软目标”匹配常采用的平方误差的损失函数的一阶泰勒展开。

注意到在上面的表达中，将损失函数拆分成了两部分：一部分是普通的蒸馏法在样本下的损失函数；另一部分就代表了雅可比匹配的损失。高阶项可以被忽略。值得注意的是对于分段线性的网络，误差项为零。另一个相似的结论是对于交叉熵的损失函数而言：

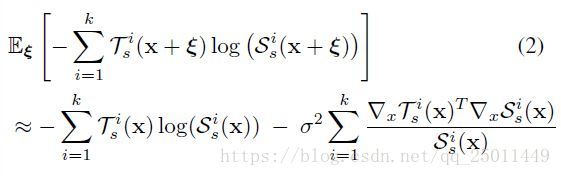
在这里高阶项也被忽略了。同时这里的$\mathcal T^i_s(x)$指的是输出经过了softmax或者sigmoid激活之后的值（也可能加了温度超参$T$，这么说的话前面的$\mathcal T^i(x)$指的是logits？）。这表明雅可比匹配的损失函数并不需要被单独地指明，它是在激活值匹配和带有噪声的模型中自然出现的（噪声难道就是指被忽略的高阶项？存疑）。这一观测结果可以在实际中通过选择感兴趣的特定噪声模型来选择适当的损失函数来应用。

这些表述表明，雅可比匹配是一个自然的结果，它不仅匹配给定数据点上的原始网络输出，而且匹配附近无限多个数据点。如图1所示，它显示通过匹配一个噪声增强的数据集，学生网络能够更好地模仿教师网络。

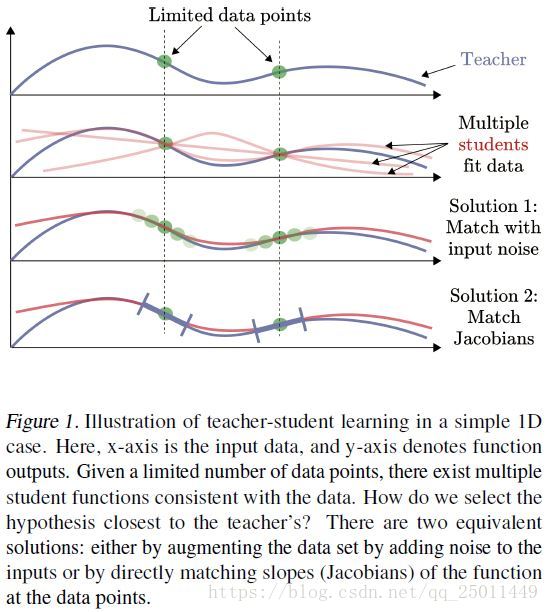
对于常规神经网络训练，我们也可以利用噪声增强的概念来推导正则项。这些正则项试图使模型对输入中添加的少量噪声具有健壮性。

命题2是对于训练一般的神经网络使用的平方误差损失函数进行一阶泰勒展开。Bishop曾提出类似于命题2的说法，他观察到线性模型的正则项与著名的Tikhonov正则项完全对应。这一正则项也由Drucker & Le Cun提出。神经网络的$l_2$权值衰减正则化可以由分层使用此正则项来得到。然而，确保噪声的鲁棒性更合适的方法是惩罚雅可比矩阵的模而不是权值。对于交叉熵误差，我们也可以得到类似的结果如下：

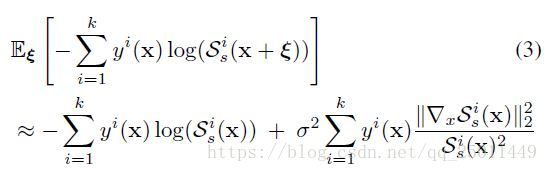
同样的，正则项涉及的$\mathcal S_s^i(x)$也是将sigmoid或softmax用在最后一层的$\mathcal S^i(x)$上。得到以上的结果只需要使用简单的一阶泰勒展开，同时在公式3中对log函数适用二阶展开。

注意，我们可以把交叉熵误差的惩罚写成更稳定的数值形式。总的来说，我们发现对平方误差的惩罚效果更好，而且更容易调整。因此，我们用平方误差损失进行蒸馏。

为什么雅可比矩阵匹配能提高性能呢?其中一个原因是，雅可比矩阵匹配是由激活值匹配损失函数与噪声的期望值得到的，而在实际中计算这种期望损失函数是非常困难的。然而，它可以通过对大量的噪声实例(即蒙特卡罗近似)的平均值来近似。这是一种带有噪声的数据扩充形式。因此，利用雅可比矩阵匹配，我们可以分析地执行一个难以处理的数据扩充过程。

4.1. Approximating the Full Jacobian

可以看出，在命题1和2的情况下，我们需要计算完整的雅可比矩阵。这样的计算量是很大的，有时是不必要的。例如，公式3只要求$y^i(x)$为非零的项。

一般来说，我们可以把雅可比矩阵的项和近似为雅可比矩阵中最大的项。但是，如果不计算整个雅可比矩阵我们就不能估计它。因此，我们使用启发式的算法，其中唯一涉及正确答案$c\in[1,k]$的输出变量被用来计算雅可比矩阵。这对应于方程3。或者，如果我们不想使用标签，我们可以使用最大的输出变量，因为它通常对应于正确的标签(对于好的模型来说)。

5. Transfer Learning

在计算机视觉领域，迁移学习通常是先使用一个庞大的数据集预训练一个网络，然后再用另外的数据集微调这个预训练的网络，这样一来，两个网络的架构必然相同，使得这种方法有一定的局限性。作者想要找到一种迁移学习方法使得预训练网络和目标网络可以为任意架构。

一种方法就是信息蒸馏，通过匹配教师网络和学生网络的输出激活值，进行训练。然而，这种方法不具有一般性，因为两者所用的数据集并不一定共享相同的标签。为了解决这个问题，可以设计学生网络，使得它有两组输出（两组输出的分支），一个是使用较小的数据集中的标签空间，另一个使用较大数据集中的标签空间。这种方法的损失函数有两项组成，每一项对应着一个输出分支。这样做有两个目的：（1）在目标数据集中和真实值的标签相匹配；（2）在目标数据集中将教师网络和学生网络的激活值相匹配，如图2所示。值得注意的是，损失函数值仅由目标数据集中的数据求算出，与原始数据集无关。这就与蒸馏法不同了，蒸馏法在同一数据集下训练，而LwF（Learning without Forgetting）可以在不同的数据集中训练。

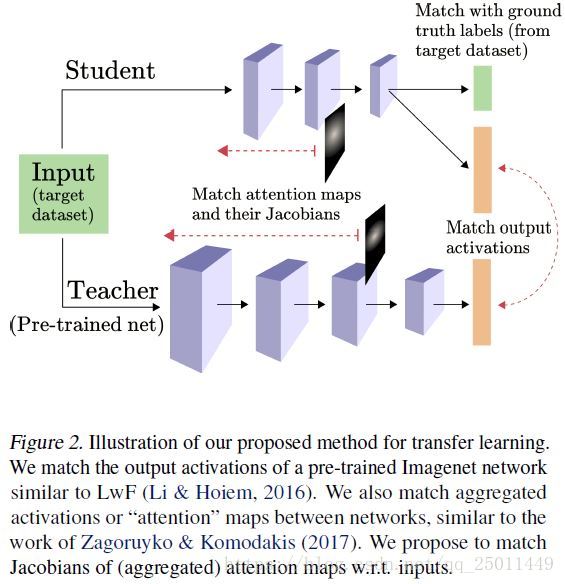
这使得将雅可比矩阵匹配框架应用于LwF变得有问题。对于蒸馏法，添加输入噪声(或雅可比矩阵匹配)可以改善整体匹配，如图1所示。对于LwF的情况，教师与学生之间的匹配程度的提高是否必然会提高转移学习效果尚不明确。这是因为教师没有对目标数据集进行训练，并且可能会在这个不可见的数据集上产生噪声或不正确的结果。为了解决这种不确定性，应该将LwF和蒸馏法联系起来。

5.1. LwF as Distillation

在下面的讨论中，将只考虑LwF方法的类似蒸馏法的的损失函数，而忽略与ground truth标签匹配的分支。要使LwF正常工作，教师网络在目标训练集上的输出激活值，必须包含着源数据集中的信息。LwF的吸引力在于，这是在没有显式使用Imagenet的情况下完成的。在这里，我们声明LwF在Imagenet的一部分上近似于蒸馏。

接下来引入了两个概念Lipschitz continuity和Hausdorff distance（非对称，即单向Hausdorff distance）如下：

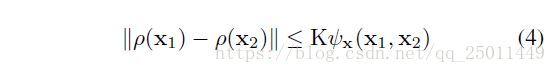
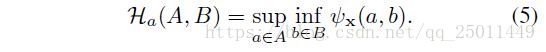
根据以上的定义可得出以下命题：

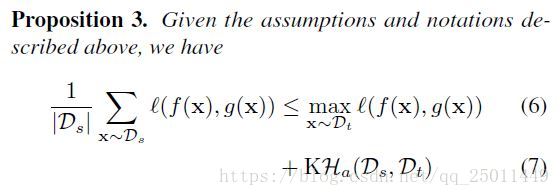
公式（6）左端即蒸馏损失函数（因为考虑了教师网络和学生网络的差距），右端是损失函数中最大的一项。注意LwF的损失函数是测试集上的平均损失。如预期的，松弛变量（公式（7））取决于原始数据和目标数据的差距（单向Hausdorff distance）。这就将有关LwF的损失函数和蒸馏损失函数相绑定。如果说Hausdorff distance很小的话（原始数据和目标数据的差距不大），那么等式左端的蒸馏损失也会被限制。值得注意的是，这个不等式也可以被看作是蒸馏的学习理论泛化范围，方法是用蒸馏的训练和测试集代替源和目标数据集。（这个想法还挺有趣的）

实际上，目标数据集通常比Imagenet小得多，并且具有不同的总体统计信息。例如，目标数据集可以是受限的花卉图像数据集。在这种情况下，我们可以将源数据集限制到它的最佳子集，特别是去掉所有不相关的样本(那些远离目标数据集的样本)。这将使Hausdorff距离更小，并提供更贴合的边界。在作者的示例中，这涉及到仅对Imagenet保留花卉。

这也很直观：如果源数据集和目标数据集完全不同，我们不期望迁移学习(LwF)会有所帮助。源数据集与目标数据集的重叠越大，Hausdorff距离越小，边界越贴合，我们越期待知识迁移的帮助。我们的结果准确地捕捉到了这种直觉。此外，这预示着Lipschitz-smooth教师神经网络在源图像和目标图像之间产生较小的特征距离，有望在迁移学习中取得较好的效果。有趣的是，Lipschitz-smooth与转移学习有关。

更重要的是，这建立了LwF作为一个近似的蒸馏方法。下面的结果将激发输入噪声添加到目标数据集。

此引理的证明可以参见有关Hausdorff距离的博文。

综上所述，作者已经证明了与LwF损失(最大损失)相关的损失是真正蒸馏损失的上限。因此，通过最小化上界，也可以期望降低蒸馏损失。

5.1.1. INCORPORATING JACOBIAN MATCHING

关键点来了，作者要把雅可比匹配加进来了。

现在输入噪声和雅可比匹配都被激发了（is well motivated这咋翻译比较好），我们可以把这些损失合并到LwF中。当在实际的深度网络中实现这个时，发现优化器根本不能减少雅可比矩阵的损失。作者推测在二阶梯度BP时遇到了vanishing gradient effect / network degeneracy（可以参考我的这篇博客）。因此，我们需要另一种方法来匹配雅可比矩阵。

5.2. Matching attention maps

仅仅匹配老师和学生网络之间的输出激活通常是不够的，特别是当两个网络都很深的时候。在这种情况下，我们也可以考虑匹配中间特征映射。一般来说，不可能匹配任意教师和学生网络之间的完整特性映射，因为它们可能具有不同的体系结构，而且特性大小可能永远不会在任何层都匹配。然而，对于现代卷积架构，某些特性的空间大小常常在架构之间匹配，即使通道的数量不匹配。Zagoruyko & Komodakis注意到，在这种情况下，它有助于匹配频道聚合激活值，他们称之为 attention maps。具体来说，这种聚合是通过对特征激活值$Z$通道的绝对值的平方求和来完成的，并由以下公式给出——

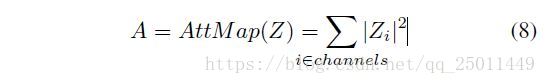
进一步，损失函数变为：

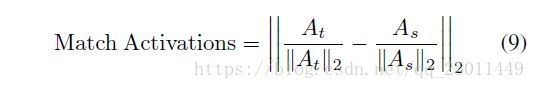
其中$A_t$和$A_s$分别为教师网络和学生网络的attention maps。损失函数的选择在这里是很严格的。

5.2.1. INCORPORATING JACOBIAN LOSS

由于激活映射具有较大的空间维度，因此计算完整的雅可比矩阵的开销非常大。因此，我们使用与前面讨论的相同的方法来计算雅可比矩阵。在本例中，这会导致在attention map中选出最大的像素，并计算这个量相对于输入的雅可比矩阵。我们index $(i, j)$计算教师网络的最大值像素，使用相同的索引来计算学生的雅可比矩阵。然后我们使用公式（9）作为损失函数：

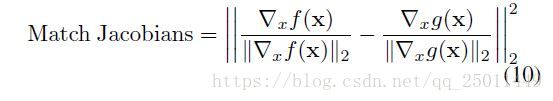
6. Experiments

实验结果感兴趣的可以参考原论文中的数据和图表。

7. Conclusion

在本文中，作者考虑匹配深神经网络的雅可比矩阵进行知识迁移。将雅可比匹配看作是一种带有高斯噪声的数据增强形式，它激发了雅可比矩阵的使用，并告诉了我们要使用怎样的损失函数。作者还将最近的迁移学习方法(LwF)与蒸馏法联系起来，使我们能够结合雅可比矩阵匹配进行迁移学习。

尽管作者取得了进步，基于蒸馏的方法和使用预训练的网络进行迁移学习的oracle法之间仍然有很大的差距。未来的工作可以集中于通过考虑更多结构化的数据增强形式而不是简单的噪音添加来缩小这一差距。