MATLAB基础教程（6）——使用matlab求解线性方程组

目录

今日任务：

一般方程：

方程组（目前仅讨论方程个数和未知数个数一样的情况）：

额外知识 

咦，咋跑题了

左除和右除

今日总结：

---

今日任务：

在数学中经常遇见的一个问题就是方程求解，特别是线性代数中，很经常遇见线性方程组的求解问题，今天就来用Matlab来探讨线性方程组的求解问题。

一般方程：

一般来讲，我们看到的方程都是这个样式的：，其中a、b都是常数，很显然，这时候 x 的解就是b/a。

也就是说，我们拿后面的值除以前面的系数，即可得到解X。

方程组（目前仅讨论方程个数和未知数个数一样的情况）：

刚刚我们讲的是一般方程，那推广到线性方程组，假设我们现在有个这样的方程：

相信大家运用高中知识也能很快的求出这个方程的答案，但是，如果四阶？五阶甚至更高呢?不如转换为矩阵的方法。

根据线性代数的知识，我们可以得到这样一个增广矩阵：

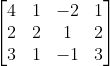
那我们令系数矩阵是A，结果矩阵是B，这个解矩阵X该怎么算呢?

额外知识 

此部分提供给还未学过线性代数的同学看，如果知道基本知识可以先行跳过。

上面的矩阵方程可以视为这样的矩阵方程：