李宏毅机器学习——Deep learning

历史

1. 1958年：感知机（线性模型）
2. 1980s：多层感知机
3. 1986：Backpropagation
4. 1989：1 hidden layer is “good enough”，why deep？
5. 2006：受限玻尔兹曼机（突破）
6. 2009：GPU

STEP

1. define a set of function
   给定网络结构，相当于定义函数集
   得到参数后一个network就是一个function
2. goodness of function
   比如 交叉熵
3. pick the best function
   梯度下降，算微分用 反向传播

反向传播

链式法则
Case1$$y=g(x),z=h(y)\to \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$$ Case2 $$x=g(s),y=h(s),z=k(x,y)\to \frac{dz}{ds}=\frac{dz}{dx}\frac{dx}{ds}+\frac{dz}{dy}\frac{dy}{ds}$$

Keras

step1: define a function set

model = Sequential()
model.add( Dense( input_dim = 28*28, output_dim = 500 ))
model.add( Activation ('sigmoid')) %可以换别的softplus,softsign,relu,tanh,linear...
model.add( Dense( output_dim = 500 ))
model.add( Activation ('sigmoid')) 
model.add( Dense( output_dim = 10))
model.add( Activation ('softmax')) 

step2 goodness of function
定义loss
step3.1 Configuration——optimizer, 比如SGD,RMSprop,Adagrad,Adadelta,Adam,Adamax,Nadam

model.compile( loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])

不同的损失函数选择：https://keras.io/objectives/
step3.2 Find the optimal parameters

model.fit( x_train, y_train, batch_size = 100, nb_epoch = 20)

其中的数据为numpy array, 行放样本，列放feature（每一列代表一个样本）
ps: 小的batch size意味着一个epoch中更多次的更新，影响速度

保存和加载模型
https://keras.io/getting-started/faq/#how-can-i-save-a-keras-model

测试
case 1:

score = model.evaluate (x_test, y_test)
print('Total loss on Testing Set:', score[0])
print('Accuracy of Testing Set:', score[1])

case2:

result = model.predict(x_test)

Keras 2.0

model.add( Dense( input_dim = 28*28, output_dim = 500 ))

改为

model.add( Dense( input_dim = 28*28, units = 500, activation  = 'sigmoid' ))

技巧

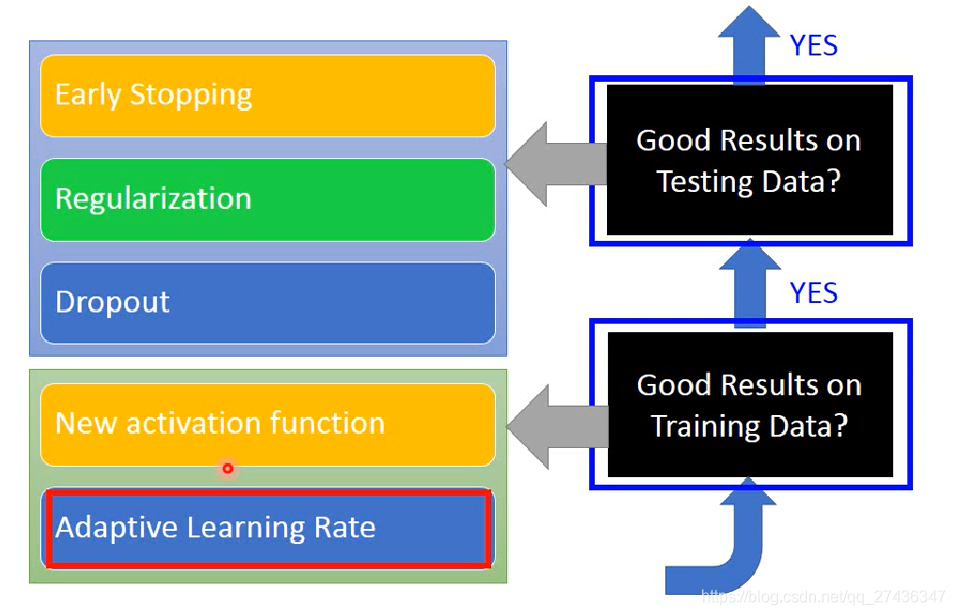
1. 先在训练集上看结果，结果不好重新训练
2. 训练集训练好了，在测试集不好就overfitting

层数太深会导致梯度消失（Vanishing Gradient Problem）现象来自sigmoid函数使得梯度衰减
ReLU可以handle梯度消失问题，相当于缩小后的线性网络
Maxout网络是自动学activation function（ReLU是Maxout的特例），可以学出的是分段线性函数

RMSProp

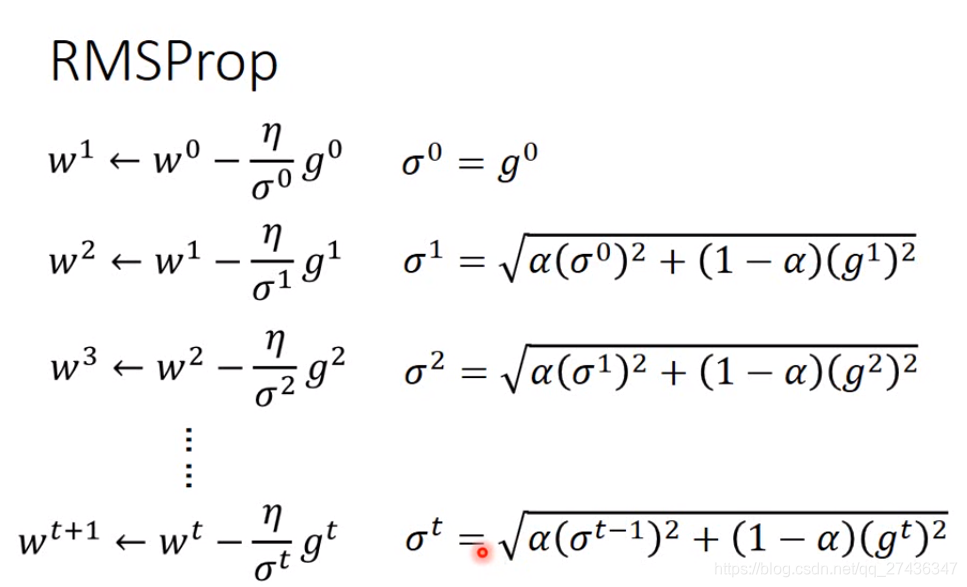
Momentum：把惯性的概念带入梯度下降
考虑现在的梯度和前一次移动的方向

Adam = RMSProp+Momentum

考虑测试集

1. Early Stopping
   应该停在testing误差最小的地方，所以用validation set的error来验证，如果validation set的loss不再减小则应该停止trainning.
   Keras提供了相应功能 http://keras.io/getting-started/faq/#how-can-i-interrupt-training-when-the-validation-loss-isnt-decreasing-anymore

2. 正则化

• L2正则化，没有用的参数最后变为0，Weight Decay（百分比递减）
  $$w^{t+1}\leftarrow (1-\eta \lambda )w^t-\eta \frac{\partial \mathrm{L}}{\partial w}$$

• L1正则化，参数大于0就减去一个数，小于0就加上一个数，使得接近0（绝对值递减）
  $$w^{t+1}\leftarrow w^t-\eta \frac{\partial \mathrm{L}}{\partial w}-\eta \lambda \mathrm{sgn}\left(w^t\right)$$

3. dropout抓爆（属于ensemble的一种）
   训练时，抓爆时，结构改变
   测试时不抓爆，要改变weigh,乘(1-p)%