Hybrid A* （混合A*）路径规划算法

总结

HybridAStar算法主要是在A* 基础上考虑车辆动力学相关的搜索算法，其放弃了A* 中对搜索空间离散化，利用Dubins或者Reeps-Shepp来考虑自车能够前进的位置，使得规划的轨迹满足车辆的非完整性约束，但是该Hybrid A* 牺牲了算法的完备性和最优性。
1.在连续空间上扩张节点搜索最短路径
2.路径平滑
Hybrid A* 算法与A* 算法的差异对比如下表所示
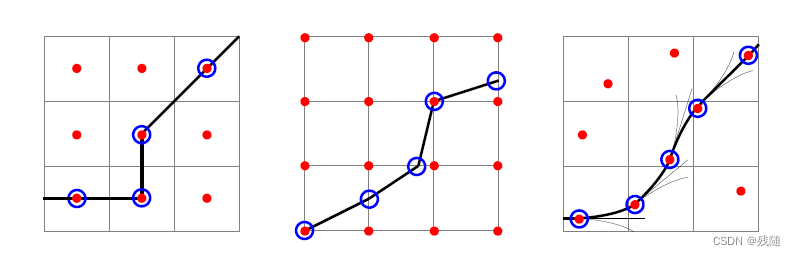
如下图所示，最左侧图是A算法的结果，最右侧是Hybrid A算法。（中间为A* 算法变种）

Hybrid A* 算法结构与A*算法流程极其类似，核心区别在于(1)生成子节点，(2)启发式函数设计。其伪代码如下

车辆非完整性约束

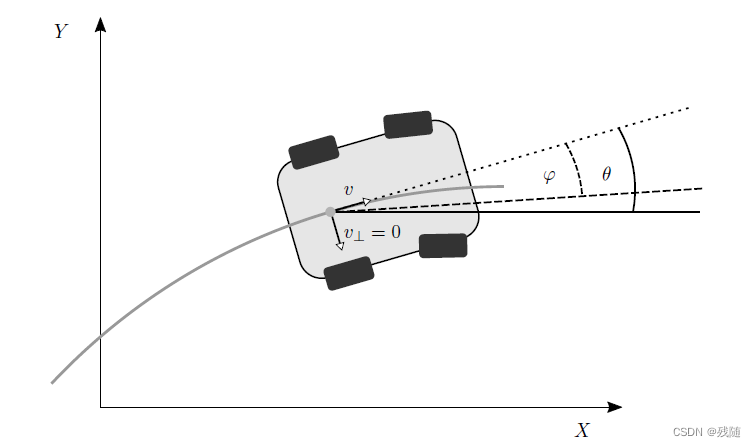
假设简单单车运动学模型

可以发现车辆运动需要满足下列的条件：

节点扩展

节点扩展主要是利用不同转弯角度生成不同的短距离节点，首先会根据局部轨迹是否碰撞决定是否评估该节点。如果无碰撞，可以利用生成节点的弧长来决定cost，当然也可以考虑转向带来的cost和行进方向变化的cost。

对于每个子节点，考虑节点到达的格子，
1.如果节点到达格子，且该格子不在closed set，表明这个格子还未被扩展，那么继续扩展评估。

2.如果格子不在open set (表明这个格子还未被之前任意节点扩展到达)且如果父节点的cost-so-far加上扩展到子节点到当前格子的cost小于当前节点的cost-so-far, 该新节点被认为是父节点的子节点， 同时更新g函数，并利用启发式函数估计cost-to-come，同时把子节点加入到open set.

启发式函数

Hybrid A*中使用两种启发式函数: constrained heuristic和unconstrained heuristic，其代表不同的节点扩展(expansion)的方式。

Constrained heuristic考虑车辆非完全性限制忽略环境障碍物。该启发式函数考虑车辆当前方向角(heading)和转向半径(turning radius)，为了自车接近目标节点时候能够保持正确的姿态。常用的启发式函数值可以使用Dubins和Reeps-Shepp曲线计算两点之间的最短距离，所以该启发式函数式是可接受的(admissible)。

Unconstrained heuristic只考虑障碍物忽视车辆非完全性限制。该启发式函数可以完全基于当前点到目标点的最短路径距离计算。常用的启发式函数可以使用欧式距离等，所以该启发式函数也是可接受的(admissible)。

因为两个启发式函数都是可接受的，只需要去两者之间的最大值作为最终的启发式函数值。

其中，l ( x )为扩展节点距离函数， d(x,xg​)为当前节点到目标节点之间的函数。

为了提高算法的效率，该启发函数值可以被存在查找表(lookup table)。

路径平滑