option-critic 架构

最新推荐文章于 2024-10-28 08:00:00 发布

oni小涛

最新推荐文章于 2024-10-28 08:00:00 发布

阅读量2.8k

点赞数 8

分类专栏：文献强化学习

强化学习同时被 2 个专栏收录

19 篇文章

订阅专栏

文献

12 篇文章

订阅专栏

时域抽象（Temporal abstraction）是拓展强化学习中学习和规划的关键。虽然在对时域上扩展的行为进行规划已经有了很好的理解，但是从数据中自主地创建这样的抽象仍然具有挑战性。我们在选项（option）框架中解决了这个问题[Sutton，Precup＆Singh，1999; Precup，2000]。我们推导得出了option的策略权重定理，并提出了一个新的 option - critic 架构，能够学习option的内部策略和终止条件，与option 策略相结合，而无需提供任何额外的奖励或子目标。离散和连续环境中的实验结果展示了框架的灵活性和效率。

介绍

时域抽象允许表示在不同时间尺度发生的行动过程的知识。在强化学习中，选项（Sutton，Precup和Singh 1999; Precup 2000）提供了一个框架，用于定义这些行动方案，并用它们无缝地学习和规划。在过去的15年中，自主发现时间抽象一直是广泛研究的主题（McGovern和Barto 2001; Stolle和Precup 2002; Menache，Mannor和Shimkin 2002;Säims¸ek和Barto 2009; Silver和Ciosek 2012）但是，可以自然地使用连续状态和/或动作空间的方法最近才开始变得可行（Konidaris等人2011; Niekum 2013; Mann，Mannor和Precup 2015; Mankowitz，Mann和Mannor 2016; Kulkarni等人2016; Vezhnevets等人2016; Daniel等人2016）。

大多数现有工作的重点是寻找子目标（代理应达到的有用状态），然后学习实现这些目标的策略。这个想法导致了有趣的方法，但由于它们的“组合”味道，这些方法也难以扩大规模。另外，与子目标相关的学习策略在数据和计算时间方面可能是高昂的;在最坏的情况下，它可能与解决整个任务一样代价高昂。

我们提出了另一种观点，它模糊了从学习选项中发现选项的问题之间的界限。基于策略梯度定理（Sutton et al.2000），我们得出了新的结果，这些结果使得能够逐步学习内部策略和终止函数，同时实施策略。在离散或连续状态和动作空间下，该方法自然地与线性和非线性函数逼近器一起工作。从单一任务中学习时，现有的学习选项方法要慢得多：大部分好处来自于在类似任务中重用学习选项。相比之下，我们表明我们的方法能够成功地在单个任务中学习选项，而不会导致任何减速，同时仍然为转移学习提供好处。

我们首先回顾与我们工作的两个主要成分相关的背景：策略梯度方法和选项。然后，我们描述了我们方法的核心思想：选项内策略和终止梯度定理。其他技术细节包含在附录中。我们提出实验结果表明我们的方法以有效的方式学习有意义的时间扩展行为。与其他方法相反，我们只需要指定所需选项的数量;没有必要有子目标，额外奖励，演示，多个问题或任何其他特殊的便利（但是，如果需要，该方法可以利用伪奖励功能）。据我们所知，这是第一种学习选项的端到端方法，可以在相当的效率下扩展到非常大的领域。

2. 预备知识和表示形式

马尔可夫决策过程包括一组状态S，一组动作A，一个过渡函数P：S×A→（S→[0,1]）和一个奖励函数r：S×A→R。我们使用离散状态集和动作集发展我们的想法。但是，我们的结果使用通常的测量理论假设情况下可以延伸到连续空间（我们的一些实证结果是在连续任务中的）。（马尔可夫静止）策略是以状态为条件的动作的概率分布，π：S×A→[0,1]。在折扣问题中，策略π的值函数被定义为预期收益：，它的动作价值函数定义为。如果，则策略π对于给定的动作值函数Q是贪心的。在离散MDP中，至少有一个就其自身的动作值函数而言是贪心的的最优策略。

策略梯度方法（Sutton等人2000; Konda和Tsitsiklis 2000）通过执行随机梯度下降来优化特定的参数化随机策略族πθ的性能目标，解决了找到良好策略的问题。策略梯度定理（Sutton等人，2000）提供了关于θ的平均奖励和折现奖励目标的梯度的表达式。在折扣设置中，目标是相对于指定的开始状态（或分布）s0定义的：ρ（θ，s0）= .策略梯度定理表明。其中，是从s0的状态开始沿着轨迹的折扣加权。在实践中，策略梯度是根据策略上的固定分布的样本估算的。（Thomas 2014）表明忽略这种固定分布中的折扣因子使得通常的策略梯度估计有偏差。但是，纠正这种差异也会降低数据效率。为简单起见，我们建立在（Sutton等人2000）的框架之上，并讨论如何根据（Thomas 2014）扩展我们的结果。

选项框架（Sutton，Precup和Singh 1999; Precup 2000）正式确定了时域拓展行动的概念。马尔可夫选项ω∈Ω是三元组（Iω，πω，βω），其中Iω⊆S是起始集合，πω是内部选项策略，并且βω：S→[0,1]是终止函数。我们还假设∀s∈S，∀ω∈Ω：s∈Iω（即，所有选项在任何地方都可用），这是在大多数选项发现算法中做出的假设。我们将在最后一节讨论如何免除这个假设。（Sutton，Precup和Singh，1999; Precup，2000）表明，由一组选项组成的MDP是半马尔可夫决策过程（Puterman 1994，第11章），它有对应的最优价值函数V_Ω（s）和最优选项-价值函数Q_Ω（s，ω）。 MDP的学习和规划算法在此设置中具有相应的算法。然而，底层MDP的存在提供了并行学习许多不同选项的可能性：这是我们在工作中利用的选项内学习的想法。

3. 学习选项

我们对学习选项的问题采取持续的观点。在任何时候，我们都希望将所有可用的经验提炼到我们系统的每个组成部分：价值函数和选项组成的策略，选项内策略和终止函数。为了实现这一目标，我们专注于学习选项策略和终止函数，假设它们使用可微分的参数化函数逼近器来表示。

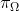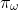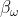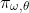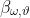我们考虑调用和返回选项执行模型，其中代理根据其对选项 $\pi_\Omega$ 的策略选择选项 $\omega$ ，然后遵循选项内策略 $\pi_\omega$ 直到终态（由 $\beta_\omega$ 指示），此时重复这一过程。 $\pi_{\omega,\theta}$ 是由θ和 $\beta_{\omega, \vartheta}$ 参数化的选项ω的选项内策略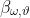， $\beta_{\omega, \vartheta}$ 是由 $\vartheta$ 参数化的选项 $\omega$ 的终止函数。我们展示了两个新的学习选项的结果，使用策略梯度定理作为蓝图获得（Sutton等，2000）。两个结果都是在假设目标是学习最大化当前任务的预期回报的选项的情况下得出的。但是，如果想要为目标函数添加额外的信息，只要它以附加的可微函数的形式出现，就可以很容易地完成。

假设我们的目标是直接优化折扣回报，在指定状态 s_0 和选项 $\omega _ 0$ 开始的所有轨迹上求期望：。请注意，此返回值取决于关于选项的策略，以及选项策略和终止函数的参数。我们将针对θ和 $\vartheta$ 采用该目标的梯度。为了做到这一点，我们将操作类似于选项内学习中使用的方程（Sutton，Precup和Singh 1999，第8节）。具体来说，选项价值函数的定义可以写成：

（1）

其中是在状态选项对的上下文中执行动作的价值：

（2）

注意，（s，ω）对导致增广状态空间，参见（Levy和Shimkin 2011）。但是，我们不会明确地使用这个空间;它仅用于简化派生。函数被称为选项 - 价值函数upon arrival（Sutton，Precup和Singh 1999，等式20）。进入状态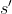时执行ω的价值由下式给出：

（3）

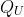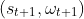请注意， Q_U 和U都取决于θ和 $\vartheta$ ，但为了清晰，我们不在说明中包含这些。推导出策略梯度所需的最后一个因素是马尔可夫链，其中估计了表现指标。自然的方法是考虑在增广状态空间中定义的链，因为状态选项对现在在通常的马尔可夫链中扮演常规状态的角色。如果选项 $\omega_t$ 已经启动或正在状态 s_t 的时间 t 执行，那么一步转换到 $\left ( s_{t+1},\omega_{t+1} \right )$ 的概率是：

(4)
显然，（4）给出的过程是同质的。在温和的条件下，并且选项随处可用，它实际上是遍历的，并且存在关于状态选项对的唯一的固定分布。
我们现在将计算期望折扣回报相对于选项内策略的参数θ的梯度，假设它们是随机且可微的。从（1,2）得出：

我们可以使用（3）和（4）进一步扩展右侧，产生以下定理：

定理1（选项内策略梯度定理）。给定一组马尔可夫选项，其随机选项内政策在其参数θ中是可微分的，预期折现收益相对于θ和初始条件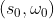 $\left ( s_{0},\omega_{0} \right )$ 的梯度为：

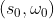其中是沿 $\left ( s_{0},\omega_{0} \right )$ 起始的轨迹的状态选项对的折扣加权：。
证名在附录中。此梯度描述了原始级别的本地更改对全局预期折扣回报的影响。相比之下，子目标或伪奖励方法假设选项的目标只是优化其自身的奖励函数，忽略提议的更改将如何在整体目标中传播。

我们现在将注意力转向终止函数的计算梯度，假设这次是随机的和可微分的。从（1,2,3）开始，我们有：

因此，关键量是U的梯度。这是调用和返回执行的自然结果，其中终止函数的“良好性”只能在进入下一个状态时进行评估。相关梯度可以进一步扩展为：

（5）
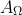其中 $A _ \Omega$ 是选项之间的优势函数（Baird 1993）。递归地扩展导致与定理（1）中类似的形式，但是其中状态 - 选项对的加权现在根据马尔可夫链移位一步（详情见附录）。
定理2（终止梯度定理）。给定一组马尔可夫选项，其随机终止函数的参数 $\vartheta$ 可微分，预期折扣回报目标相对于初始条件的梯度为：

其中是从的状态 - 选项对的折扣加权：。

当形成基线以减少梯度估计的方差时，优势函数经常出现在策略梯度方法（Sutton等人，2000）中。它在这种情况下的存在主要与算法设计有关。有趣的是，在我们的情况下，它作为推导的直接结果，并给定理一个直观的解释：当选项选择相对于所有选项的期望值不是最理想时，优势函数是负的并且它驱动梯度校正向上，这增加了终止的几率。终止后，代理有机会使用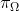 $\pi_\Omega$ 选择更好的选项。类似的想法也是选项的中断执行模型（Sutton，Precup和Singh 1999）的基础，其中只要当前选项ω的值小于，就强制终止。（Mann，Mankowitz和Mannor，2014）最近通过价值迭代设置中的中断Bellman算子镜头研究了中断选项。终止梯度定理可以解释为提供基于梯度的中断贝尔曼算子。

4.算法架构

图1：option-critic体系结构图。选项执行模型由触点上的开关⊥描绘。仅当当前选项终止时，才会根据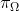 $\pi_\Omega$ 选择新选项。

基于定理1和2，我们现在可以设计用于学习选项的随机梯度下降算法。使用双时间框架（Konda和Tsitsiklis 2000），我们建议在快速时间范围内学习值，同时以较慢的速率更新选项内策略和终止函数。
我们将结果系统称为option-critic架构，参考actor-critic架构（Sutton 1984）。内部选项策略，终止函数和策略选项属于系统的actor部分，而critic由Q_U和A_Ω组成。option-critic架构没有规定如何获得π_Ω，因为各种现有方法都适用：在SMDP级别使用策略梯度方法，在选项模型上使用规划器，或使用时间差分更新。如果π_Ω是对选项的贪婪策略，则从（2）得出相应的一步异策略（off-policy）更新目标是：

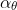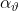这也是（Sutton，Precup和Singh 1999）的选项内Q学习算法的更新目标。使用选项内Q学习的选项评论的原型实现在算法1中示出。表格式的设定仅为了清楚呈现。我们分别将critic，选项内策略和终止函数的学习率写为α， $\alpha _\theta$ 和 $\alpha_\vartheta$ 。
算法1：选项评论与表格内选项Q学习

除了Q_Ω之外，学习Q_U在参数和样本的数量方面在计算上也都是不划算的。一个实际的解决方案是只学习Q_Ω并从中得出Q_U的估计值。因为Q_U是对下一个状态的期望，所以，由此得出是适当的估计量。我们选择这种方法进行Arcade学习环境中的深度神经网络实验。

5. 实验

我们首先考虑四房间领域的导航任务（Sutton，Precup和Singh 1999）。我们的目标是评估一组完全自主学习的选项的能力，以便从环境的突然变化中恢复。（Sutton，Precup和Singh，1999）对一组预先指定的选项进行了类似的实验;我们的结果中的选项尚未被先验地指定。

最初目标位于东门口，初始状态从所有其他单元格均匀绘制。在1000个片段之后，目标移动到右下方的随机位置。原始运动可能以1/3的概率失败，在这种情况下，代理随机地转换到空的相邻单元之一。折扣系数为0.99，奖励在目标时为+1，否则为0。我们选择使用Boltzmann分布和带有sigmoid函数的终止来参数化选项内策略。选项策略是使用选项内Q学习来学习的。我们还使用玻尔兹曼策略实现了原始的actor-critic（表示为AC-PG）。我们还将option-critic与使用玻尔兹曼探索的原始SARSA代理进行了比较，不使用任何资格迹。对于所有Boltzmann策略，我们将温度参数设置为0.001。所有权重都初始化为零。

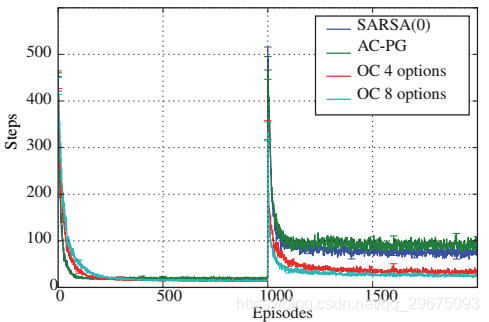
图2：1000个片段之后，四房间域中的目标位置随机移动。option-critic（“OC”）比原始actor-critic（“AC-PG”）和SARSA（0）恢复得更快。每条线平均超过350次运行。

从图2中可以看出，当目标突然改变时，option-critic代理恢复得更快。此外，初始选项集是以与原始方法相当的速率从头开始学习的。尽管领域很简单，但我们还没有看到其他可以解决这一任务而不会产生比仅使用原始动作大得多的成本的方法，（McGovern和Barto 2001;Säimsek和Barto 2009）。

图3：option-critic代理学习的终止概率有4个选项。最暗的颜色代表环境中的墙壁，而较浅的颜色代表较高的终止概率。

在两个时域拓展的设置中，有4个选项和8个选项，终止事件更可能发生在门口附近（图3），同意他们认为它们是好的子目标。与（Sutton，Precup和Singh 1999）相反，我们自己并没有对这些知识进行编码，只是让代理找到最大化预期折扣回报的选项。

5.1 弹球领域

图4：弹球：使用4个选项在250次训练后发现的解决方案的样本轨迹所有选项（颜色编码）都由策略用于成功轨迹中的选项。初始状态位于左上角，目标位于右下角（红色圆圈）。

在弹球领域（Konidaris和Barto 2009），球必须通过任意形状的多边形迷宫引导到指定的目标位置。状态空间在x-y平面中球的位置和速度上是连续的。在每一步中，代理必须在五个离散的原始动作中进行选择：在垂直或水平方向上移动球更快或更慢，或采取空动作。与障碍物的碰撞是弹性的并且可以被代理利用。在该域中，当重复选择空动作时，阻力系数0.995在有限的步之后有效地停止球运动。每次推力动作都会受到-5的惩罚，而不采取行动费用-1。当代理到达目标时，该片段终止于+10000奖励。我们中断了超过10000步的片段并将折扣系数设置为0.99。

我们在critic中使用了内部选项Q学习，其中线性函数逼近了三阶傅立叶基（Konidaris等人，2011），我们进行了2个，3个或4个选项的实验。我们用Boltzmann策略作为选项内策略，线性S形函数作为终止函数。critic的学习率设定为0.01，内部和终止梯度的学习率设定为0.001。我们对选项间使用了 $\epsilon$ = 0.01的epsilon-greedy策略。

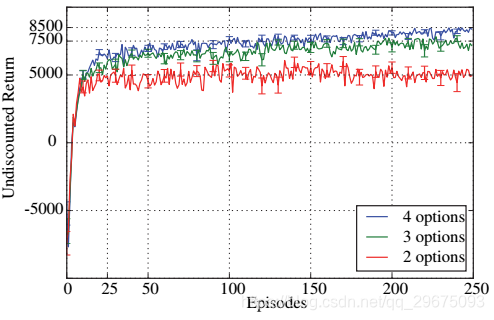
图5：Pinball域中的学习曲线。

在（Konidaris和Barto 2009）中，只有在10个片段的酝酿期后才能使用和更新选项。随着学习完全融入option-critic，在40个片段中，已经在所有环境中学习了近乎最佳的选项集。从定性的角度来看，这些选项表现出时域拓展和专业化（图4）。我们还观察到，在许多成功的轨迹中，红色选项将始终用于目标附近。

5.2 街机学习环境

我们在街机学习环境（ALE）（Bellemare等人2013）中使用option-critic架构，使用深度神经网络来近似critic并代表选项内策略和终止函数。我们使用与（Mnih等人2013）相同的配置来获得网络的前3个卷积层。我们在第一层使用了32个大小为8×8和步幅为4的卷积滤波器，64个大小为4×4的滤波器，在第二层中步长为2，在第三层中使用了步长为1的64个3×3滤波器。然后我们将第三层的输出馈送到512个神经元的密集共享层，如图6所示。我们将选项内策略和终止梯度的学习速率固定为0.00025，并将RMSProp用于critic。

图6：深度神经网络架构。最后4个图像的串联通过卷积层馈送，产生在选项内策略，终止函数和策略选项之间共享的密集表示。

我们将选项内策略表示为第四（密集）层的线性 - softmax，以便输出以当前观察为条件的动作的概率分布。使用sigmoid函数类似地定义终止函数，每个终止一个输出神经元。

批评网络使用内部选项Q学习和经验重播进行培训。选项政策和终止已在线更新。在测试阶段，我们使用-greedy策略而不是选项= 0.05（Mnih et al.2013）。

作为优化返回的结果，终止梯度趋向于随时间缩小选项。这是预期的，因为理论上原始动作足以解决任何MDP。我们通过向优势函数添加一个小的ξ= 0.01项来解决这个问题，由终止梯度使用：AΩ（s，ω）+ξ=QΩ（s，ω） - VΩ（s）+ξ。该项具有正则化效应，通过在选项的值估计与VΩ中反映的“最优”值之间施加ξ-余量。如果选项的值接近最佳值，则这使得优势函数为正，从而拉伸它。在（Mann，Mankowitz和Mannor 2014）中提出了类似的正则化器。

如（Mnih等人，2016），我们观察到选项内政策很快就会变得具有确定性。这个问题似乎与一般的深度神经网络的政策梯度方法的使用有关，而不是选项评论本身。我们通过惩罚低熵内部选项策略来应用（Mnih等人，2016）规定的正规化器。

图7：Seaquest：在梯度估计器中使用基线可以改善选项内策略中的操作分布，从而降低其确定性。每列代表Seaquest中学习的选项之一。垂直轴跨越ALE的18个原始动作。经验动作频率由强度编码。

最后，将基线Q_Ω添加到选项内策略梯度估计器中以减少其方差。如图7所示，这一变化对选项内策略分配的质量和整体代理表现产生了重大改进（Harb 2016）。

图8：街机学习环境中的学习曲线。在所有四个游戏中使用相同的参数集：8个选项，0.01终止正则化，0.01熵正则化和选项内策略梯度的基线。

我们评估了Asterisk，Ms. Pacman，Seaquest和Zaxxon的option-critic。为了进行比较，我们允许系统学习与（Mnih等人，2013）相同数量的片段，并将参数固定为所有四个域中的相同值。尽管有更多的参数需要学习，但是option-critic能够在200个片段内学习可以从头开始实现所有游戏目标的选项（图8）。在Asterisk，Seaquest和Zaxxon中，选项评论家超越了基于原始行为的原始DQN架构的性能。在每个游戏中学到的八个选项是完全端到端学习，与特征表示相结合，没有事先规定的子目标或伪奖励结构。

图9：在Seaquest中学习2个选项时，option-critic发现的解决方案中的上/下专业化。顶部栏显示游戏中的轨迹，“白色”表示选项1处于活动状态的分段，选项2代表“黑色”。

option-critic发现的解决方案很容易在Seaquest游戏中解释，只有两种选择。我们发现每个选项都专门用于行为序列，其中包括向上或向下按钮。图9显示了从一个选项到另一个选项的典型转换，首先向上选项0然后向下切换到选项1。在这个游戏中（Krishnamurthy等人2016）使用基于图分区的选项发现算法也找到了具有类似结构的选项。

6. 相关工作

由于选项发现最近受到了很多关注，我们现在更详细地讨论我们的方法相比于其他人的方法。（Comanici和Precup 2010）使用基于梯度的方法来仅改进半马尔可夫选项的终止函数;终止是通过自启动后观察到的特征的累积测量的逻辑分布来建模的。（Levy和Shimkin 2011）也建立在策略梯度方法的基础上，明确地构建增广状态空间并将停止事件视为额外的控制动作。相反，我们不需要直接构造这个（非常大的）空间。（Silver and Ciosek 2012）通过依赖组合属性将动态链接到更长的时间序列。早期关于线性选项的工作（Sorg和Singh 2010）也使用了组合性来计划使用线性期望模型的选项。我们的方法也依赖于Bellman方程和组合，但与策略梯度方法相结合。

一些最近的论文还试图将选项发现表示为一种优化问题，其解决方案与函数逼近兼容。（Daniel et al.2016）通过将终止函数视为隐藏变量并使用EM来学习它们来学习返回优化选项。（Vezhnevets等人，2016）考虑了具有开环内部选项策略的学习选项问题，也称为宏行动。与经典规划一样，缓存更频繁的动作序列。学习从状态到动作序列的映射以及承诺模块，该模块在必要时触发重新规划。相比之下，我们始终使用闭环策略，这些策略对状态信息起反应并且可以提供更好的解决方案。（Mankowitz，Mann和Mannor 2016）提出了一种基于梯度的选项学习算法，假设启动集和终止函数的特定结构。在此框架下，在状态空间的任何分区中只有一个选项处于活动状态。（Kulkarni等人，2016）使用DQN框架来实现基于梯度的选项学习者，该学习者使用内在奖励来学习选项的内部策略，并使用外在奖励来学习选项策略。与我们的框架相反，子目标的描述作为选项学习者的输入。option-critic在概念上是一般性的，并不需要学习选项的内在动机。